19.2: The Circulant Matrix- Nature of its Eigenstates

Last updated
Save as PDF

Page ID: 29520

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

The matrix we’ve constructed above has a very special property: each row is identical to the preceding row with the elements moved over one place, that is, it has the form

\begin{equation}
\left(\begin{array}{llll}
c_{0} & c_{1} & c_{2} & c_{3} \\
c_{3} & c_{0} & c_{1} & c_{2} \\
c_{2} & c_{3} & c_{0} & c_{1} \\
c_{1} & c_{2} & c_{3} & c_{0}
\end{array}\right)
\end{equation}

Such matrices are called circulants, and their properties are well known. In particular, we’ll show that the eigenvectors have the form \(\left(1, \omega_{j}, \omega_{j}^{2}, \omega_{j}^{3}, \ldots, \omega_{j}^{N-1}\right)^{T}\) where \(\omega_{j}^{N}=1\).

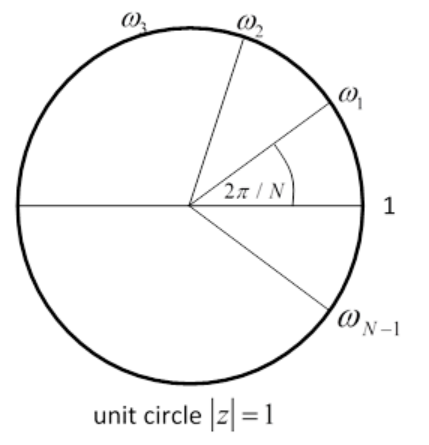
Recall the roots of the equation \(z^{N}=1\) are N points equally spaced around the unit circle, \begin{equation}
e^{2 \pi i n / N}, n=0,1,2, \ldots N-1
\end{equation}

The standard mathematical notation is to label these points \(\begin{equation}
1, \omega_{1}, \omega_{2}, \omega_{3}, \ldots, \omega_{N-1}
\end{equation}\) as shown in the figure, but notice that \(\omega_{j}=\omega_{1}^{j}\)