24.3: Rotation of a Body about a Fixed Axis

Last updated
Save as PDF

Page ID: 30514

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

As a preliminary, let’s look at a body firmly attached to a rod fixed in space, and rotating with angular velocity \(\Omega\) radians/sec. about that axis. You’ll recall from freshman physics that the angular momentum and rotational energy are \(L_{z}=I \Omega, \quad E_{\mathrm{rot}}=\frac{1}{2} I \Omega^{2}\) where

\begin{equation}
I=\sum_{i} m_{i} r_{\perp i}^{2}=\int d x d y d z \rho(x, y, z) r_{\perp}^{2}
\end{equation}

\(\text { (here } r_{\perp}=\sqrt{x^{2}+y^{2}} \text { is the distance from the axis). }\)

But you also know that both angular velocity and angular momentum are vectors. Obviously, for this example, the angular velocity is a vector pointing along the axis of rotation, \(\vec{\Omega}=\left(0,0, \Omega_{z}\right)\). One might be tempted to conclude that the angular momentum also points along the axis, but this is not always the case. An instructive example is provided by two masses m at the ends of a rod of length \(2\alpha\) held at a fixed angle \(\theta\) to the z axis, which is the axis of rotation.

Evidently,

\begin{equation}
L_{z}=2 m a^{2} \sin ^{2} \theta \cdot \Omega
\end{equation}

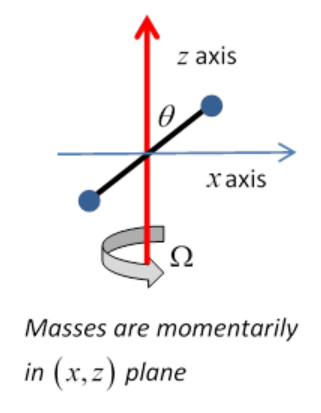
But notice that, assuming the rod is momentarily in the xz plane, as shown, then

\(\begin{equation}
L_{x}=-2 m a^{2} \cos ^{2} \theta \cdot \Omega
\end{equation}\)

The total angular momentum is not parallel to the total angular velocity!

In fact, as should be evident, the total angular momentum is rotating around the constant angular velocity vector, so the axis must be providing a torque. This is why unbalanced car wheels stress the axle.