25.2: Analyzing Rolling Motion

Kinetic Energy of a Cone Rolling on a Plane

The cone rolls without slipping on the horizontal XY plane. The momentary line of contact with the plane is OA, at an angle θ in the horizontal plane from the X axis.

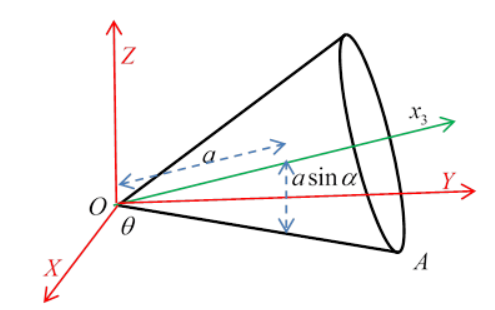
The important point is that this line of contact, regarded as part of the rolling cone, is momentarily at rest when it’s in contact with the plane. This means that, at that moment, the cone is rotating about the stationary line OA. Therefore, the angular velocity vector \(\vec{\Omega}\) points along OA.

Taking the cone to have semi-vertical angle \(\alpha\) (meaning this is the angle between OA and the central axis of the cone) the center of mass, which is a distance a from the vertex, and on the central line, moves along a circle at height \(a \sin \alpha\) above the plane, this circle being centered on the Z axis, and having radius \(a \cos \alpha\). The center of mass moves at velocity \(V=\dot{\theta} a \cos \alpha\), so contributes translational kinetic energy

\[\dfrac{1}{2} M V^{2}=\dfrac{1}{2} M \dot{\theta}^{2} a^{2} \cos ^{2} \alpha\]

Now visualize the rolling cone turning around the momentarily fixed line OA: the center of mass, at height \(a \sin \alpha\), moves at V, so the angular velocity

\[\Omega=\dfrac{V}{a \sin \alpha}=\dot{\theta} \cot \alpha.\]

Next, we first define a new set of axes with origin O: one, \(x_{3}\)is the cone’s own center line, another, \(x_{2}\) is perpendicular to that and to OA, this determines \(x_{1}\) (For these last two, since they’re through the vertex, the moment of inertia is the one worked out at the end of the previous section, see above.)

Since \(\vec{\Omega} \text { is along } O A, \text { its components with respect to these axes }\left(x_{1}, x_{2}, x_{3}\right) \text { are }(\Omega \sin \alpha, 0, \quad \Omega \cos \alpha)\)

However, to compute the total kinetic energy, for the rotational contribution we need to use a parallel set of axes through the center of mass. This just means subtracting from the vertex perpendicular moments of inertia found above a factor \(M a^{2}\).

The total kinetic energy is

\[\begin{align*} T &=\dfrac{1}{2} M \dot{\theta}^{2} a^{2} \cos ^{2} \alpha+\dfrac{1}{2} I_{1} \dot{\theta}^{2} \cos ^{2} \alpha+\dfrac{1}{2} I_{3} \dot{\theta}^{2} \dfrac{\cos ^{4} \alpha}{\sin ^{2} \alpha} \\[4pt] &=3 M h^{2} \dot{\theta}^{2}\left(1+5 \cos ^{2} \alpha\right) / 40 \end{align*}\]

using

\[I_{1}=\dfrac{3}{20} M R^{2}+\dfrac{3}{80} M h^{2}, \quad I_{3}=\dfrac{3}{10} M R^{2}, \quad a=\dfrac{3}{4} h, \quad R=h \tan \alpha\]