28.4: The Asymmetrical Top
- Page ID
- 30678
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Here we’ll generalize the above equations and argument to the general case of three different moments of inertia about the three principal axes. That is,
\begin{equation}\begin{array}{r}\dfrac{L_{1}^{2}}{I_{1}}+\dfrac{L_{2}^{2}}{I_{2}}+\dfrac{L_{3}^{2}}{I_{3}}=2 E \\
L_{1}^{2}+L_{2}^{2}+L_{3}^{2}=L^{2}\end{array}\end{equation}
We’ll take
\[I_{3}>I_{2}>I_{1}\]
From the limitations on energy for given angular momentum, the maximum sphere radius is the maximum semimajor axis of the ellipsoid, the ellipsoid touches the sphere at its two extreme poles. For a slightly smaller sphere, the lines of intersection arte two small ellipses centered at the poles, evidently the major axis will go around this elliptical cone in fixed space. At the other extreme, the minimum allowed angular momentum for a given energy, the sphere is entirely inside the ellipsoid except that it touches at the ends of the shortest axes. Again, for a top with slightly more angular momentum, it will precess (elliptically) around this minimum axis.
In both these cases, spin about the axis is stable against small perturbations. This is not the case for spin about the middle axis —for that energy, the intersection of the sphere and ellipsoid does not reduce to two points.
The equations for pure spin about the middle axis can be written
\[ \begin{array}{r}\dfrac{L_{1}^{2}}{I_{1}}+\dfrac{L_{2}^{2}}{I_{2}}+\dfrac{L_{3}^{2}}{I_{3}}=2 E \\\dfrac{L_{1}^{2}}{I_{2}}+\dfrac{L_{2}^{2}}{I_{2}}+\dfrac{L_{3}^{2}}{I_{2}}=\dfrac{L^{2}}{I_{2}}=2 E\end{array}\]
These equations define the points common to the sphere and the ellipsoid at this energy.
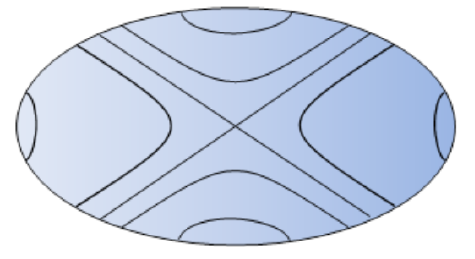
Subtracting the second from the first, we find
\[L_{1}^{2}\left(\dfrac{1}{I_{1}}-\dfrac{1}{I_{2}}\right)+L_{3}^{2}\left(\dfrac{1}{I_{3}}-\dfrac{1}{I_{2}}\right)=0\]
with solutions
\[L_{1}=\pm c L_{3}, \quad c=I_{1}\left(I_{3}-I_{2}\right) / I_{2}\left(I_{2}-I_{1}\right)\]
So for this energy and total angular momentum squared, the intersection of the sphere and ellipsoid is in two planes, both containing the intermediate axis. This means that any perturbation of this motion will send the system along one of these paths, or a trajectory close to it—in other words, it will deviate far from its original motion, in contrast to spin about either of the other two axes.
In all cases, the path followed by \(\vec{L}\), the intersection of the sphere and the ellipsoid, is closed, so the angular momentum cycles back to its original value, in periodic motion. Landau calculates the period, a straightforward (but too lengthy to repeat here) solution of Euler’s equations, giving elliptic functions. Actually, the top does not return to its original configuration: the angular momentum returns, but the top has a different angular position about its axis. Landau states this (Berry like?) result, but refers to Whittaker for the derivation.