4.3: Bifurcation and Point Attractors
- Page ID
- 9581
Interesting new phenomena, such as bifurcation, and attractors, occur when the non-linearity is large. In chapter \(3\) it was shown that the state-space diagram \(\left( \dot{x},x\right)\) for an undamped harmonic oscillator is an ellipse with dimensions defined by the total energy of the system. As shown in figure (3.5.1), for the damped harmonic oscillator, the state-space diagram spirals inwards to the origin due to dissipation of energy. Non-linearity distorts the shape of the ellipse or spiral on the state-space diagram, and thus the state-space, or corresponding phase-space, diagrams, provide useful representations of the motion of linear and non-linear periodic systems.
The complicated motion of non-linear systems makes it necessary to distinguish between transient and asymptotic behavior. The damped harmonic oscillator executes a transient spiral motion that asymptotically approaches the origin. The transient behavior depends on the initial conditions, whereas the asymptotic limit of the steady-state solution is a specific location, that is called a point attractor. The point attractor for damped motion in the anharmonic potential well
\[U(x)=2x^{2}+x^{4}\]
is at the minimum, which is the origin of the state-space diagram as shown in figure (4.2.1).
The more complicated one-dimensional potential well
\[U(x)=8-4x^{2}+0.5x^{4}\]
shown in Figure \(\PageIndex{1}\), has two minima that are symmetric about \(x=0\) with a saddle of height \(8\).
The kinetic plus potential energies of a particle with mass \(m=2,\) released in this potential, will be assumed to be given by
\[E(x,\dot{x})=\dot{x}^{2}+U(x)\]
The state-space plot in Figure \(\PageIndex{1}\) shows contours of constant energy with the minima at \((x,\dot{x})=(\pm 2,0)\). At slightly higher total energy the contours are closed loops around either of the two minima at \( x=\pm 2\). At total energies above the saddle energy of \(8\) the contours are peanut-shaped and are symmetric about the origin. Assuming that the motion is weakly damped, then a particle released with total energy \(E_{total}\) which is higher than \(E_{saddle}\) will follow a peanut-shaped spiral trajectory centered at \((x,\dot{x})=(0,0)\) in the state-space diagram for \( E_{total}>E_{saddle}\). For \(E_{total}<E_{saddle}\) there are two separate solutions for the two minimum centered at \(x=\pm 2\) and \(\dot{x} =0\). This is an example of bifurcation where the one solution for \( E_{total}>E_{saddle}\) bifurcates into either of the two solutions for \( E_{total}<E_{saddle}\).
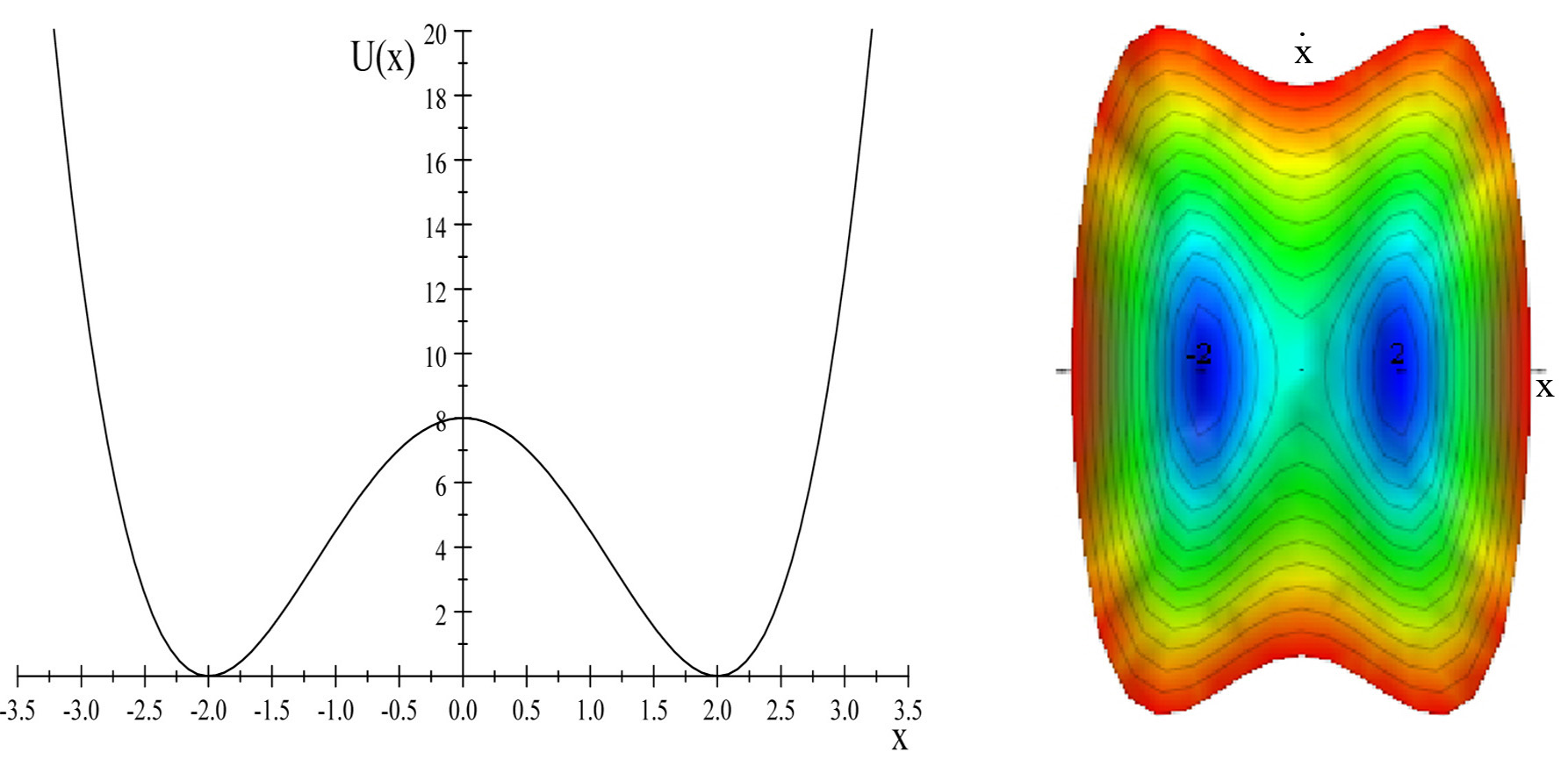
For an initial total energy \(E_{total}>E_{saddle},\) damping will result in spiral trajectories of the particle that will be trapped in one of the two minima. For \(E_{total}>E_{saddle}\) the particle trajectories are centered giving the impression that they will terminate at \((x,\dot{x})=(0,0)\) when the kinetic energy is dissipated. However, for \(E_{total}<E_{saddle}\) the particle will be trapped in one of the two minimum and the trajectory will terminate at the bottom of that potential energy minimum occurring at \((x, \dot{x})=(\pm 2,0)\). These two possible terminal points of the trajectory are called point attractors. This example appears to have a single attractor for \(E_{total}>E_{saddle}\) which bifurcates leading to two attractors at \((x,\dot{x})=(\pm 2,0)\) for \(E_{total}<E_{saddle}\). The determination as to which minimum traps a given particle depends on exactly where the particle starts in state space and the damping etc. That is, for this case, where there is symmetry about the \(x\)-axis, the particle has an initial total energy \(E_{total}>E_{saddle},\) then the initial conditions with \(\pi\) radians of state space will lead to trajectories that are trapped in the left minimum, and the other \(\pi\) radians of state space will be trapped in the right minimum. Trajectories starting near the split between these two halves of the starting state space will be sensitive to the exact starting phase. This is an example of sensitivity to initial conditions.


