Skip to main content
\(\require{cancel}\)
Physics LibreTexts

16.4: The Simple Pendulum

  1. Last updated
  2. Save as PDF
  • Page ID
    1605

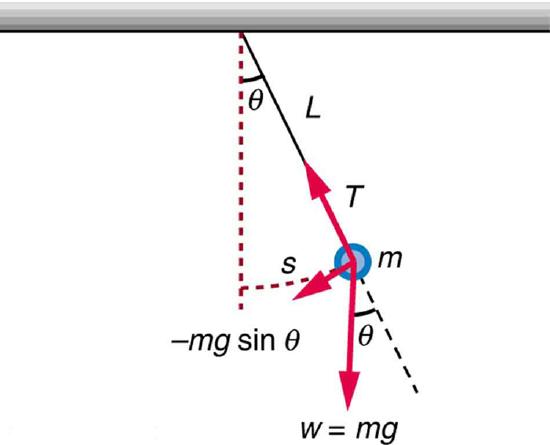
    • In the figure, a horizontal bar is drawn. A perpendicular dotted line from the middle of the bar, depicting the equilibrium of pendulum, is drawn downward. A string of length L is tied to the bar at the equilibrium point. A circular bob of mass m is tied to the end of the string which is at a distance s from the equilibrium. The string is at an angle of theta with the equilibrium at the bar. A red arrow showing the time T of the oscillation of the mob is shown along the string line toward the bar. An arrow from the bob toward the equilibrium shows its restoring force asm g sine theta. A perpendicular arrow from the bob toward the ground depicts its mass as W equals to mg, and this arrow is at an angle theta with downward direction of string.

    Figure \(\PageIndex{1}\): A simple pendulum has a small-diameter bob and a string that has a very small mass but is strong enough not to stretch appreciably. The linear displacement from equilibrium is \(s\), the length of the arc. Also shown are the forces on the bob, which result in a net force of - \(mg \, sin \, \theta \) toward the equilibrium position—that is, a restoring force.

    Pendulums are in common usage. Some have crucial uses, such as in clocks; some are for fun, such as a child’s swing; and some are just there, such as the sinker on a fishing line. For small displacements, a pendulum is a simple harmonic oscillator. A simple pendulum is defined to have an object that has a small mass, also known as the pendulum bob, which is suspended from a light wire or string, such as shown in Figure \(\PageIndex{1}\). Exploring the simple pendulum a bit further, we can discover the conditions under which it performs simple harmonic motion, and we can derive an interesting expression for its period.

    We begin by defining the displacement to be the arc length \(s\). We see from Figure \(\PageIndex{1}\) that the net force on the bob is tangent to the arc and equals \(mg \, sin \, \theta\). (The weight \(mg\) has components \(mg \, cos \, \theta\) along the string and \(mg \, sin \, \theta\) tangent to the arc.) Tension in the string exactly cancels the component \(mg \, cos \theta\) parallel to the string. This leaves a net restoring force back toward the equilibrium position at \(\theta = 0\).

    Now, if we can show that the restoring force is directly proportional to the displacement, then we have a simple harmonic oscillator. In trying to determine if we have a simple harmonic oscillator, we should note that for small angles (less than about \(15^o\)), \(sin \, \theta \approx \theta \, (sin \, \theta\) and \(\theta\) differ by about 1% or less at smaller angles). Thus, for angles less than about \(15^o\), the restoring force \(F\) is \[F \approx -mg\theta.\] The displacement \(s\) is directly proportional to \(\theta\). When \(\theta\) is expressed in radians, the arc length in a circle is related to its radius (\(L\) in this instance) by:

    \[s = L\theta,\]

    so that

    \[\theta = \dfrac{s}{L}.\]

    For small angles, then, the expression for the restoring force is:

    \[F \approx -\dfrac{mg}{L}s.\]

    This expression is of the form:

    \[F = -kx,\]

    where the force constant is given by \(k = mg/L\) and the displacement is given by \(x = s\). For angles less than about \(15^o\) the restoring force is directly proportional to the displacement, and the simple pendulum is a simple harmonic oscillator.

    Using this equation, we can find the period of a pendulum for amplitudes less than about \(15^o\). For the simple pendulum:

    \[T = 2\pi \sqrt{\dfrac{m}{k}} = 2\pi \sqrt{\dfrac{m}{mg/L}}.\]

    for the period of a simple pendulum. This result is interesting because of its simplicity. The only things that affect the period of a simple pendulum are its length and the acceleration due to gravity. The period is completely independent of other factors, such as mass. As with simple harmonic oscillators, the period \(T\) for a pendulum is nearly independent of amplitude, especially if \(\theta\) is less than about \(15^o\). Even simple pendulum clocks can be finely adjusted and accurate.

    Note the dependence of \(T\) on \(g\). If the length of a pendulum is precisely known, it can actually be used to measure the acceleration due to gravity. Consider the following example.

    Example \(\PageIndex{1}\): Measuring Acceleration due to Gravity: The Period of a Pendulum

    What is the acceleration due to gravity in a region where a simple pendulum having a length 75.000 cm has a period of 1.7357 s?

    Strategy

    We are asked to find \(g\) given the period \(T\) and the length \(L\) of a pendulum. We can solve \(T = 2\pi \sqrt{\frac{L}{g}}\) for \(g\), assuming only that the angle of deflection is less than \(15^o\).

    Solution

    1. Square \(T = 2\pi \sqrt{\frac{L}{g}}\) and solve for \(g\): \[g = 4\pi^2 \dfrac{L}{T^2}.\]
    2. Substitute known values into the new equation: \[g = 4\pi^2 \dfrac{0.75000 \, m}{(1.7357 \, s)^2}.\]
    3. Calculate to find \(g\): \[g = 9.8281 \, m/s^2.\]

    Discussion

    This method for determining \(g\) can be very accurate. This is why length and period are given to five digits in this example. For the precision of the approximation \(sin \, \theta \approx \theta\) to be better than the precision of the pendulum length and period, the maximum displacement angle should be kept below about \(0.5^o\).

    MAKING CAREER CONNECTIONS

    Knowing \(g\) can be important in geological exploration; for example, a map of \(g\) over large geographical regions aids the study of plate tectonics and helps in the search for oil fields and large mineral deposits.

    TAKE-HOME EXPERIMENT: DETERMINING \(g\)

    Use a simple pendulum to determine the acceleration due to gravity \(g\) in your own locale. Cut a piece of a string or dental floss so that it is about 1 m long. Attach a small object of high density to the end of the string (for example, a metal nut or a car key). Starting at an angle of less than \(10^o\), allow the pendulum to swing and measure the pendulum’s period for 10 oscillations using a stopwatch. Calculate \(g\). How accurate is this measurement? How might it be improved?

    Exercise \(\PageIndex{1}\): Check Your Understanding

    An engineer builds two simple pendula. Both are suspended from small wires secured to the ceiling of a room. Each pendulum hovers 2 cm above the floor. Pendulum 1 has a bob with a mass of \(10 \, kg\). Pendulum 2 has a bob with a mass of \(100 \, kg\). Describe how the motion of the pendula will differ if the bobs are both displaced by \(12^o\).

    Answer

    The movement of the pendula will not differ at all because the mass of the bob has no effect on the motion of a simple pendulum. The pendula are only affected by the period (which is related to the pendulum’s length) and by the acceleration due to gravity.

    PHET EXPLORATIONS: PENDELUM LAB

    Play with one or two pendulums and discover how the period of a simple pendulum depends on the length of the string, the mass of the pendulum bob, and the amplitude of the swing. It’s easy to measure the period using the photogate timer. You can vary friction and the strength of gravity. Use the pendulum to find the value of \(g\) on planet X. Notice the anharmonic behavior at large amplitude.

    PhET_Icon.png

    Figure \(\PageIndex{2}\): Pendulum Lab

    Glossary

    simple pendulum
    an object with a small mass suspended from a light wire or string

    Contributors

    Paul Peter Urone (Professor Emeritus at California State University, Sacramento) and Roger Hinrichs (State University of New York, College at Oswego) with Contributing Authors: Kim Dirks (University of Auckland) and Manjula Sharma (University of Sydney). This work is licensed by OpenStax University Physics under a Creative Commons Attribution License (by 4.0).