23.E: Electromagnetic Induction, AC Circuits, and Electrical Technologies (Exercise)
- Last updated
- Jul 6, 2021
- Save as PDF
- Page ID
- 15421
( \newcommand{\kernel}{\mathrm{null}\,}\)
Conceptual Questions
23.1 Induced Emf and Magnetic Flux
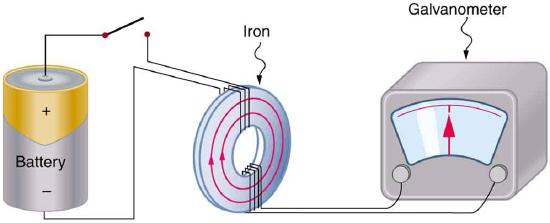
1. How do the multiple-loop coils and iron ring in the version of Faraday’s apparatus shown in Figure enhance the observation of induced emf?
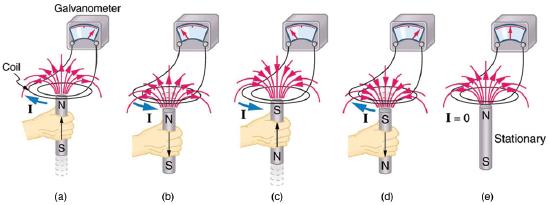
2. When a magnet is thrust into a coil as in Figure(a), what is the direction of the force exerted by the coil on the magnet? Draw a diagram showing the direction of the current induced in the coil and the magnetic field it produces, to justify your response. How does the magnitude of the force depend on the resistance of the galvanometer?
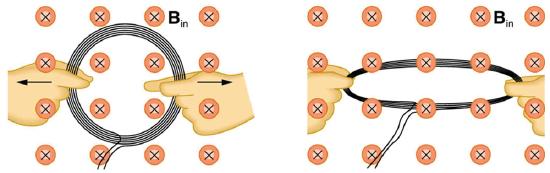
3. Explain how magnetic flux can be zero when the magnetic field is not zero.
4. Is an emf induced in the coil in Figure when it is stretched? If so, state why and give the direction of the induced current.
A circular coil of wire is stretched in a magnetic field.
23.2 Faraday’s Law of Induction: Lenz’s Law
5. A person who works with large magnets sometimes places her head inside a strong field. She reports feeling dizzy as she quickly turns her head. How might this be associated with induction?
6. A particle accelerator sends high-velocity charged particles down an evacuated pipe. Explain how a coil of wire wrapped around the pipe could detect the passage of individual particles. Sketch a graph of the voltage output of the coil as a single particle passes through it.
23.3 Motional Emf
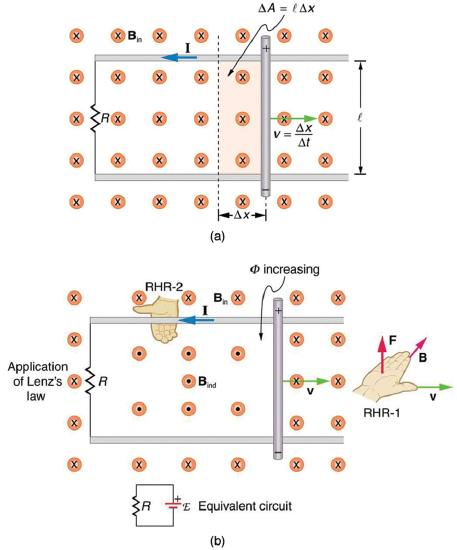
7. Why must part of the circuit be moving relative to other parts, to have usable motional emf? Consider, for example, that the rails in Figure are stationary relative to the magnetic field, while the rod moves.
8. A powerful induction cannon can be made by placing a metal cylinder inside a solenoid coil. The cylinder is forcefully expelled when solenoid current is turned on rapidly. Use Faraday’s and Lenz’s laws to explain how this works. Why might the cylinder get live/hot when the cannon is fired?
9. An induction stove heats a pot with a coil carrying an alternating current located beneath the pot (and without a hot surface). Can the stove surface be a conductor? Why won’t a coil carrying a direct current work?
10. Explain how you could thaw out a frozen water pipe by wrapping a coil carrying an alternating current around it. Does it matter whether or not the pipe is a conductor? Explain.
23.4 Eddy Currents and Magnetic Damping
11. Explain why magnetic damping might not be effective on an object made of several thin conducting layers separated by insulation.
12. Explain how electromagnetic induction can be used to detect metals? This technique is particularly important in detecting buried landmines for disposal, geophysical prospecting and at airports.
23.5 Electric Generators
13. Using RHR-1, show that the emfs in the sides of the generator loop in Figure are in the same sense and thus add.
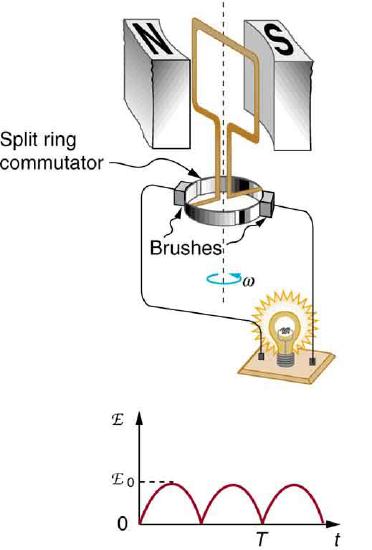
14. The source of a generator’s electrical energy output is the work done to turn its coils. How is the work needed to turn the generator related to Lenz’s law?
23.6 Back Emf
15. Suppose you find that the belt drive connecting a powerful motor to an air conditioning unit is broken and the motor is running freely. Should you be worried that the motor is consuming a great deal of energy for no useful purpose? Explain why or why not.
23.7 Transformers
16. Explain what causes physical vibrations in transformers at twice the frequency of the AC power involved.
23.8 Electrical Safety: Systems and Devices
17. Does plastic insulation on live/hot wires prevent shock hazards, thermal hazards, or both?
18. Why are ordinary circuit breakers and fuses ineffective in preventing shocks?
19. A GFI may trip just because the live/hot and neutral wires connected to it are significantly different in length. Explain why.
23.9 Inductance
20. How would you place two identical flat coils in contact so that they had the greatest mutual inductance? The least?
21. How would you shape a given length of wire to give it the greatest self-inductance? The least?
22. Verify, as was concluded without proof in Example, that units of T⋅m2/A=Ω⋅s=H.
23.11 Reactance, Inductive and Capacitive
23. Presbycusis is a hearing loss due to age that progressively affects higher frequencies. A hearing aid amplifier is designed to amplify all frequencies equally. To adjust its output for presbycusis, would you put a capacitor in series or parallel with the hearing aid’s speaker? Explain.
24. Would you use a large inductance or a large capacitance in series with a system to filter out low frequencies, such as the 100 Hz hum in a sound system? Explain.
25. High-frequency noise in AC power can damage computers. Does the plug-in unit designed to prevent this damage use a large inductance or a large capacitance (in series with the computer) to filter out such high frequencies? Explain.
26. Does inductance depend on current, frequency, or both? What about inductive reactance?
27. Explain why the capacitor in Figure(a) acts as a low-frequency filter between the two circuits, whereas that in Figure(b) acts as a high-frequency filter.
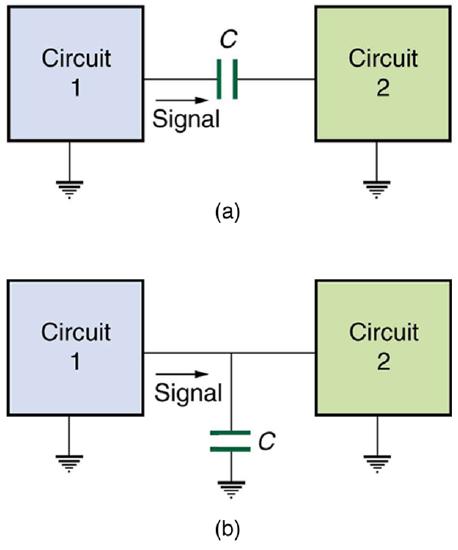
Capacitors and inductors. Capacitor with high frequency and low frequency.
28. If the capacitors in Figure are replaced by inductors, which acts as a low-frequency filter and which as a high-frequency filter?
23.12 RLC Series AC Circuits
29. Does the resonant frequency of an AC circuit depend on the peak voltage of the AC source? Explain why or why not.
30. Suppose you have a motor with a power factor significantly less than 1. Explain why it would be better to improve the power factor as a method of improving the motor’s output, rather than to increase the voltage input.
Problems & Exercises
23.1 Induced Emf and Magnetic Flux
31. What is the value of the magnetic flux at coil 2 in Figure due to coil 1?
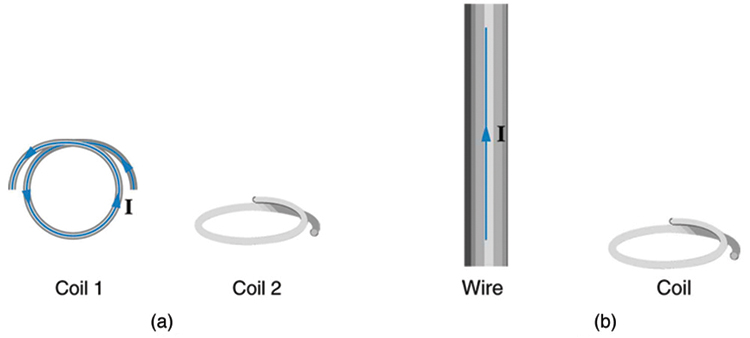
(a) The planes of the two coils are perpendicular. (b) The wire is perpendicular to the plane of the coil.
Solution
Zero
32. What is the value of the magnetic flux through the coil in Figure(b) due to the wire?
23.2 Faraday’s Law of Induction: Lenz’s Law
33. Referring to Figure(a), what is the direction of the current induced in coil 2:
(a) If the current in coil 1 increases?
(b) If the current in coil 1 decreases?
(c) If the current in coil 1 is constant? Explicitly show how you follow the steps in the Problem-Solving Strategy for Lenz's Law.
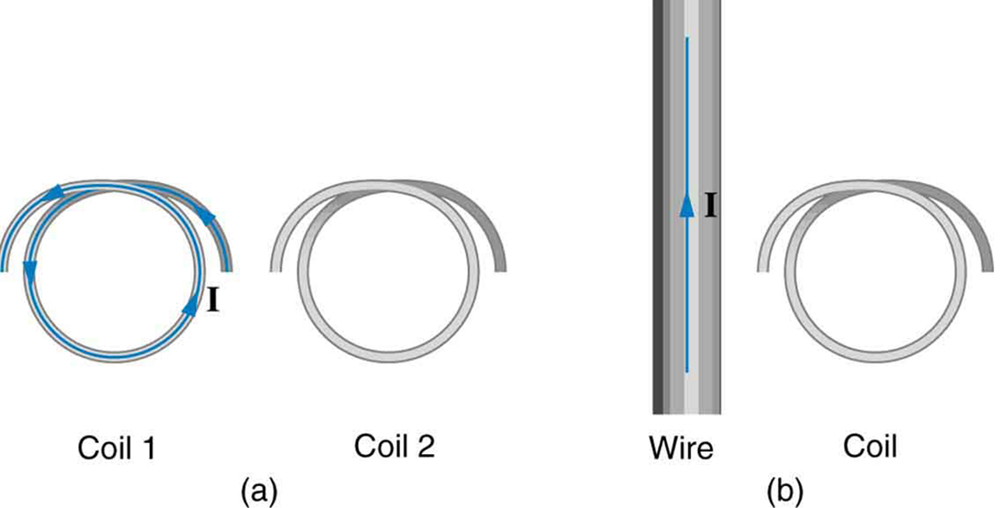
(a) The coils lie in the same plane. (b) The wire is in the plane of the coil
Solution
(a) CCW
(b) CW
(c) No current induced
34. Referring to Figure(b), what is the direction of the current induced in the coil:
(a) If the current in the wire increases?
(b) If the current in the wire decreases?
(c) If the current in the wire suddenly changes direction? Explicitly show how you follow the steps in the Problem-Solving Strategy for Lenz’s Law.
35. Referring to Figure, what are the directions of the currents in coils 1, 2, and 3 (assume that the coils are lying in the plane of the circuit):
(a) When the switch is first closed?
(b) When the switch has been closed for a long time?
(c) Just after the switch is opened?
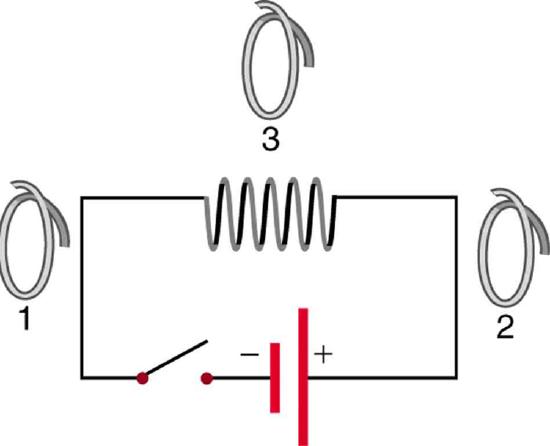
Solution
(a) 1 CCW, 2 CCW, 3 CW
(b) 1, 2, and 3 no current induced
(c) 1 CW, 2 CW, 3 CCW
36. Repeat the previous problem with the battery reversed.
37. Verify that the units of ΔΦ/Δt are volts. That is, show that 1T⋅m2/s=1V.
38. Suppose a 50-turn coil lies in the plane of the page in a uniform magnetic field that is directed into the page. The coil originally has an area of 0.250m2. It is stretched to have no area in 0.100 s. What is the direction and magnitude of the induced emf if the uniform magnetic field has a strength of 1.50 T?
39. (a) An MRI technician moves his hand from a region of very low magnetic field strength into an MRI scanner’s 2.00 T field with his fingers pointing in the direction of the field. Find the average emf induced in his wedding ring, given its diameter is 2.20 cm and assuming it takes 0.250 s to move it into the field. (b) Discuss whether this current would significantly change the temperature of the ring.
Solution
(a) 3.04 mV
(b) As a lower limit on the ring, estimate R = 1.00 mΩ. The heat transferred will be 2.31 mJ. This is not a significant amount of heat.
40. Integrated Concepts
Referring to the situation in the previous problem:
(a) What current is induced in the ring if its resistance is 0.0100 Ω?
(b) What average power is dissipated?
(c) What magnetic field is induced at the center of the ring? (d) What is the direction of the induced magnetic field relative to the MRI’s field?
41. An emf is induced by rotating a 1000-turn, 20.0 cm diameter coil in the Earth’s 5.00×10−5T magnetic field. What average emf is induced, given the plane of the coil is originally perpendicular to the Earth’s field and is rotated to be parallel to the field in 10.0 ms?
Solution
0.157 V
42. A 0.250 m radius, 500-turn coil is rotated one-fourth of a revolution in 4.17 ms, originally having its plane perpendicular to a uniform magnetic field. (This is 60 rev/s.) Find the magnetic field strength needed to induce an average emf of 10,000 V.
43. Integrated Concepts
Approximately how does the emf induced in the loop in Figure(b) depend on the distance of the center of the loop from the wire?
Solution
proportional to 1r
44. Integrated Concepts
(a) A lightning bolt produces a rapidly varying magnetic field. If the bolt strikes the earth vertically and acts like a current in a long straight wire, it will induce a voltage in a loop aligned like that in Figure(b). What voltage is induced in a 1.00 m diameter loop 50.0 m from a 2.00×106lightning strike, if the current falls to zero in 25.0μs?
(b) Discuss circumstances under which such a voltage would produce noticeable consequences.
23.3 Motional Emf
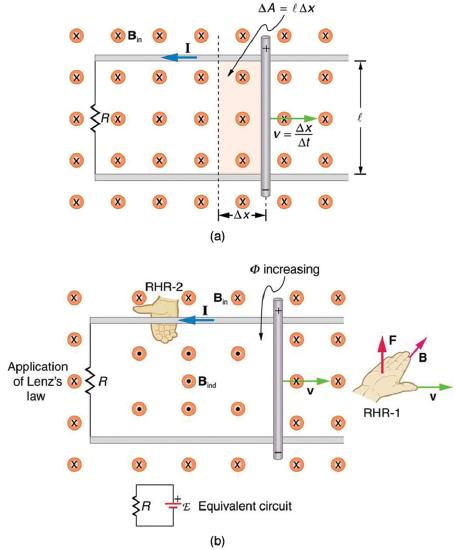
45. Use Faraday’s law, Lenz’s law, and RHR-1 to show that the magnetic force on the current in the moving rod in Figure is in the opposite direction of its velocity.
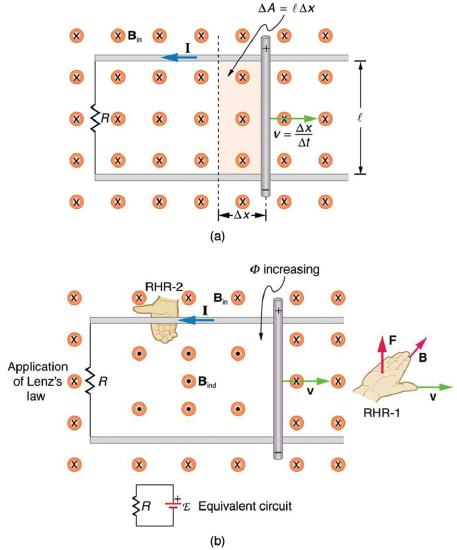
46. If a current flows in the Satellite Tether shown in Figure, use Faraday’s law, Lenz’s law, and RHR-1 to show that there is a magnetic force on the tether in the direction opposite to its velocity.
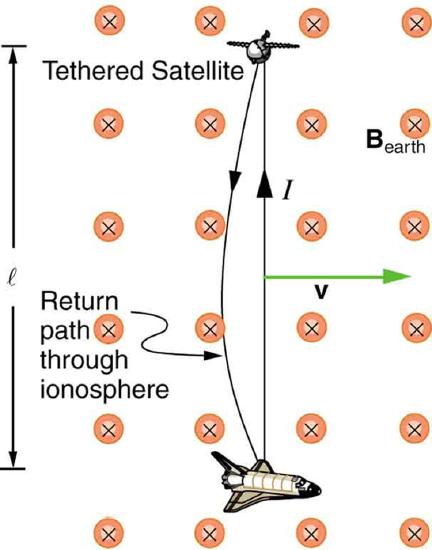
47. (a) A jet airplane with a 75.0 m wingspan is flying at 280 m/s. What emf is induced between wing tips if the vertical component of the Earth’s field is 3.00×10−5T?
(b) Is an emf of this magnitude likely to have any consequences? Explain.
Solution
(a) 0.630 V
(b) No, this is a very small emf.
48. (a) A nonferrous screwdriver is being used in a 2.00 T magnetic field. What maximum emf can be induced along its 12.0 cm length when it moves at 6.00 m/s?
(b) Is it likely that this emf will have any consequences or even be noticed?
49. At what speed must the sliding rod in Figure move to produce an emf of 1.00 V in a 1.50 T field, given the rod’s length is 30.0 cm?
Solution
2.22 m/s
50. The 12.0 cm long rod in Figure moves at 4.00 m/s. What is the strength of the magnetic field if a 95.0 V emf is induced?
51. Prove that when B,ℓ, and v are not mutually perpendicular, motional emf is given by emf=Bℓvsinθ. If v is perpendicular to B, then θ is the angle between ℓ and B. If ℓ is perpendicular to B, then θ is the angle between v and B.
52. In the August 1992 space shuttle flight, only 250 m of the conducting tether considered in Example could be let out. A 40.0 V motional emf was generated in the Earth’s 5.00×10−5T field, while moving at 7.80×103m/s. What was the angle between the shuttle’s velocity and the Earth’s field, assuming the conductor was perpendicular to the field?
53. Integrated Concepts
Derive an expression for the current in a system like that in Figure, under the following conditions. The resistance between the rails is R , the rails and the moving rod are identical in cross section A and have the same resistivity ρ. The distance between the rails is l, and the rod moves at constant speed v perpendicular to the uniform field B. At time zero, the moving rod is next to the resistance R .
54. Integrated Concepts
The Tethered Satellite in Figure has a mass of 525 kg and is at the end of a 20.0 km long, 2.50 mm diameter cable with the tensile strength of steel.
(a) How much does the cable stretch if a 100 N force is exerted to pull the satellite in? (Assume the satellite and shuttle are at the same altitude above the Earth.)
(b) What is the effective force constant of the cable?
(c) How much energy is stored in it when stretched by the 100 N force?
55. Integrated Concepts
The Tethered Satellite discussed in this module is producing 5.00 kV, and a current of 10.0 A flows.
(a) What magnetic drag force does this produce if the system is moving at 7.80 km/s?
(b) How much kinetic energy is removed from the system in 1.00 h, neglecting any change in altitude or velocity during that time?
(c) What is the change in velocity if the mass of the system is 100,000 kg?
(d) Discuss the long term consequences (say, a week-long mission) on the space shuttle’s orbit, noting what effect a decrease in velocity has and assessing the magnitude of the effect.
Solution
(a) 10.0 N
(b) 2.81×108J
(c) 0.36 m/s
(d) For a week-long mission (168 hours), the change in velocity will be 60 m/s, or approximately 1%. In general, a decrease in velocity would cause the orbit to start spiraling inward because the velocity would no longer be sufficient to keep the circular orbit. The long-term consequences are that the shuttle would require a little more fuel to maintain the desired speed, otherwise the orbit would spiral slightly inward.
23.4 Eddy Currents and Magnetic Damping
56. Make a drawing similar to Figure, but with the pendulum moving in the opposite direction. Then use Faraday’s law, Lenz’s law, and RHR-1 to show that magnetic force opposes motion.
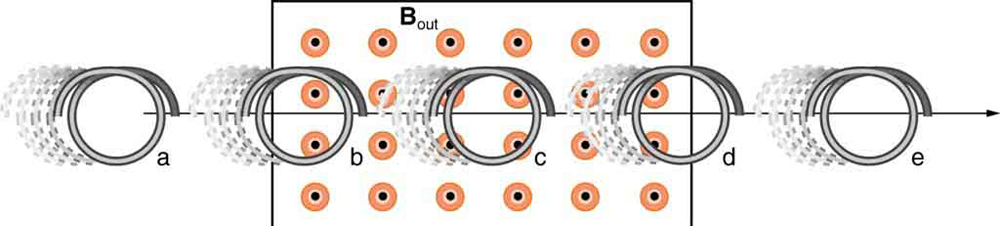
A coil is moved into and out of a region of uniform magnetic field.
57. A coil is moved through a magnetic field as shown in Figure. The field is uniform inside the rectangle and zero outside. What is the direction of the induced current and what is the direction of the magnetic force on the coil at each position shown?
23.5 Electric Generators
58. Calculate the peak voltage of a generator that rotates its 200-turn, 0.100 m diameter coil at 3600 rpm in a 0.800 T field.
Solution
474 V
59. At what angular velocity in rpm will the peak voltage of a generator be 480 V, if its 500-turn, 8.00 cm diameter coil rotates in a 0.250 T field?
60. What is the peak emf generated by rotating a 1000-turn, 20.0 cm diameter coil in the Earth’s 5.00×10−5T magnetic field, given the plane of the coil is originally perpendicular to the Earth’s field and is rotated to be parallel to the field in 10.0 ms?
Solution
0.247 V
61. What is the peak emf generated by a 0.250 m radius, 500-turn coil is rotated one-fourth of a revolution in 4.17 ms, originally having its plane perpendicular to a uniform magnetic field. (This is 60 rev/s.)
62. (a) A bicycle generator rotates at 1875 rad/s, producing an 18.0 V peak emf. It has a 1.00 by 3.00 cm rectangular coil in a 0.640 T field. How many turns are in the coil?
(b) Is this number of turns of wire practical for a 1.00 by 3.00 cm coil?
Solution
(a) 50
(b) yes
63. Integrated Concepts
This problem refers to the bicycle generator considered in the previous problem. It is driven by a 1.60 cm diameter wheel that rolls on the outside rim of the bicycle tire.
(a) What is the velocity of the bicycle if the generator’s angular velocity is 1875 rad/s?
(b) What is the maximum emf of the generator when the bicycle moves at 10.0 m/s, noting that it was 18.0 V under the original conditions?
(c) If the sophisticated generator can vary its own magnetic field, what field strength will it need at 5.00 m/s to produce a 9.00 V maximum emf?
64. (a) A car generator turns at 400 rpm when the engine is idling. Its 300-turn, 5.00 by 8.00 cm rectangular coil rotates in an adjustable magnetic field so that it can produce sufficient voltage even at low rpms. What is the field strength needed to produce a 24.0 V peak emf?
(b) Discuss how this required field strength compares to those available in permanent and electromagnets.
Solution
(a) 0.477 T
(b) This field strength is small enough that it can be obtained using either a permanent magnet or an electromagnet.
65. Show that if a coil rotates at an angular velocity ω, the period of its AC output is 2π/ω.
66. A 75-turn, 10.0 cm diameter coil rotates at an angular velocity of 8.00 rad/s in a 1.25 T field, starting with the plane of the coil parallel to the field.
(a) What is the peak emf?
(b) At what time is the peak emf first reached?
(c) At what time is the emf first at its most negative?
(d) What is the period of the AC voltage output?
Solution
(a) 5.89 V
(b) At t=0
(c) 0.393 s
(d) 0.785 s
67. (a) If the emf of a coil rotating in a magnetic field is zero at t=0, and increases to its first peak at t=0.100ms, what is the angular velocity of the coil?
(b) At what time will its next maximum occur?
(c) What is the period of the output?
(d) When is the output first one-fourth of its maximum?
(e) When is it next one-fourth of its maximum?
68. Unreasonable Results
A 500-turn coil with a 0.250m2 area is spun in the Earth’s 5.00×10−5T field, producing a 12.0 kV maximum emf.
(a) At what angular velocity must the coil be spun?
(b) What is unreasonable about this result?
(c) Which assumption or premise is responsible?
Solution
(a) 1.92×106rad/s
(b) This angular velocity is unreasonably high, higher than can be obtained for any mechanical system.
(c) The assumption that a voltage as great as 12.0 kV could be obtained is unreasonable.
23.6 Back Emf
69. Suppose a motor connected to a 120 V source draws 10.0 A when it first starts.
(a) What is its resistance?
(b) What current does it draw at its normal operating speed when it develops a 100 V back emf?
Solution
(a) 12.00 Ω
(b) 1.67 A
70. A motor operating on 240 V electricity has a 180 V back emf at operating speed and draws a 12.0 A current. (a) What is its resistance? (b) What current does it draw when it is first started?
71. What is the back emf of a 120 V motor that draws 8.00 A at its normal speed and 20.0 A when first starting?
Solution
72.0 V
72. The motor in a toy car operates on 6.00 V, developing a 4.50 V back emf at normal speed. If it draws 3.00 A at normal speed, what current does it draw when starting?
73. Integrated Concepts
The motor in a toy car is powered by four batteries in series, which produce a total emf of 6.00 V. The motor draws 3.00 A and develops a 4.50 V back emf at normal speed. Each battery has a 0.100Ω internal resistance. What is the resistance of the motor?
Solution
0.100 Ω
23.7 Transformers
74. A plug-in transformer, like that in Figure, supplies 9.00 V to a video game system.
(a) How many turns are in its secondary coil, if its input voltage is 120 V and the primary coil has 400 turns?
(b) What is its input current when its output is 1.30 A?
Solution
(a) 30.0
(b) 9.75×10−2A
75. An American traveler in New Zealand carries a transformer to convert New Zealand’s standard 240 V to 120 V so that she can use some small appliances on her trip.
(a) What is the ratio of turns in the primary and secondary coils of her transformer?
(b) What is the ratio of input to output current?
(c) How could a New Zealander traveling in the United States use this same transformer to power her 240 V appliances from 120 V?
76. A cassette recorder uses a plug-in transformer to convert 120 V to 12.0 V, with a maximum current output of 200 mA.
(a) What is the current input?
(b) What is the power input?
(c) Is this amount of power reasonable for a small appliance?
Solution
(a) 20.0 mA
(b) 2.40 W
(c) Yes, this amount of power is quite reasonable for a small appliance.
77. (a) What is the voltage output of a transformer used for rechargeable flashlight batteries, if its primary has 500 turns, its secondary 4 turns, and the input voltage is 120 V?
(b) What input current is required to produce a 4.00 A output? (c) What is the power input?
78. (a) The plug-in transformer for a laptop computer puts out 7.50 V and can supply a maximum current of 2.00 A. What is the maximum input current if the input voltage is 240 V? Assume 100% efficiency.
(b) If the actual efficiency is less than 100%, would the input current need to be greater or smaller? Explain.
Solution
(a) 0.063 A
(b) Greater input current needed.
79. A multipurpose transformer has a secondary coil with several points at which a voltage can be extracted, giving outputs of 5.60, 12.0, and 480 V.
(a) The input voltage is 240 V to a primary coil of 280 turns. What are the numbers of turns in the parts of the secondary used to produce the output voltages?
(b) If the maximum input current is 5.00 A, what are the maximum output currents (each used alone)?
80. A large power plant generates electricity at 12.0 kV. Its old transformer once converted the voltage to 335 kV. The secondary of this transformer is being replaced so that its output can be 750 kV for more efficient cross-country transmission on upgraded transmission lines.
(a) What is the ratio of turns in the new secondary compared with the old secondary?
(b) What is the ratio of new current output to old output (at 335 kV) for the same power?
(c) If the upgraded transmission lines have the same resistance, what is the ratio of new line power loss to old?
Solution
(a) 2.2
(b) 0.45
(c) 0.20, or 20.0%
81. If the power output in the previous problem is 1000 MW and line resistance is 2.00Ω, what were the old and new line losses?
82. Unreasonable Results
The 335 kV AC electricity from a power transmission line is fed into the primary coil of a transformer. The ratio of the number of turns in the secondary to the number in the primary is Ns/Np=1000.
(a) What voltage is induced in the secondary?
(b) What is unreasonable about this result?
(c) Which assumption or premise is responsible?
Solution
(a) 335 MV
(b) way too high, well beyond the breakdown voltage of air over reasonable distances
(c) input voltage is too high
83. Construct Your Own Problem
Consider a double transformer to be used to create very large voltages. The device consists of two stages. The first is a transformer that produces a much larger output voltage than its input. The output of the first transformer is used as input to a second transformer that further increases the voltage. Construct a problem in which you calculate the output voltage of the final stage based on the input voltage of the first stage and the number of turns or loops in both parts of both transformers (four coils in all). Also calculate the maximum output current of the final stage based on the input current. Discuss the possibility of power losses in the devices and the effect on the output current and power.
23.8 Electrical Safety: Systems and Devices
84. Integrated Concepts
A short circuit to the grounded metal case of an appliance occurs as shown in Figure. The person touching the case is wet and only has a 3.00kΩ resistance to earth/ground.
(a) What is the voltage on the case if 5.00 mA flows through the person?
(b) What is the current in the short circuit if the resistance of the earth/ground wire is 0.200Ω?
(c) Will this trigger the 20.0 A circuit breaker supplying the appliance?
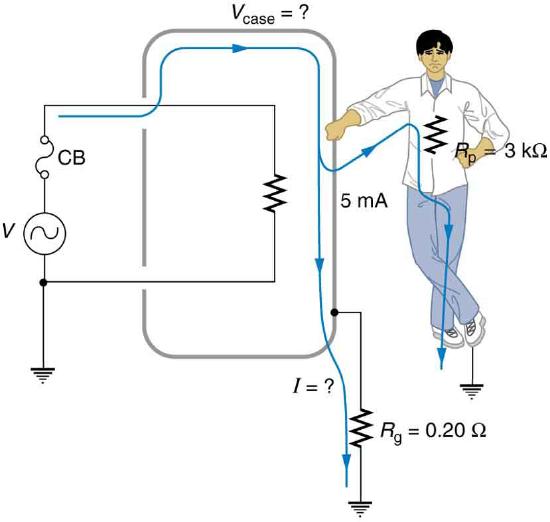
A person can be shocked even when the case of an appliance is grounded. The large short circuit current produces a voltage on the case of the appliance, since the resistance of the earth/ground wire is not zero.
Solution
(a) 15.0 V
(b) 75.0 A
(c) yes
23.9 Inductance
85. Two coils are placed close together in a physics lab to demonstrate Faraday’s law of induction. A current of 5.00 A in one is switched off in 1.00 ms, inducing a 9.00 V emf in the other. What is their mutual inductance?
Solution
1.80 mH
86. If two coils placed next to one another have a mutual inductance of 5.00 mH, what voltage is induced in one when the 2.00 A current in the other is switched off in 30.0 ms?
87. The 4.00 A current through a 7.50 mH inductor is switched off in 8.33 ms. What is the emf induced opposing this?
Solution
3.60 V
88. A device is turned on and 3.00 A flows through it 0.100 ms later. What is the self-inductance of the device if an induced 150 V emf opposes this?
89. Starting with emf2=−MΔI1Δt, show that the units of inductance are (V⋅s)/A=Ω⋅s.
90. Camera flashes charge a capacitor to high voltage by switching the current through an inductor on and off rapidly. In what time must the 0.100 A current through a 2.00 mH inductor be switched on or off to induce a 500 V emf?
91. A large research solenoid has a self-inductance of 25.0 H.
(a) What induced emf opposes shutting it off when 100 A of current through it is switched off in 80.0 ms?
(b) How much energy is stored in the inductor at full current?
(c) At what rate in watts must energy be dissipated to switch the current off in 80.0 ms?
(d) In view of the answer to the last part, is it surprising that shutting it down this quickly is difficult?
Solution
(a) 31.3 kV
(b) 125 kJ
(c) 1.56 MW
(d) No, it is not surprising since this power is very high.
92. (a) Calculate the self-inductance of a 50.0 cm long, 10.0 cm diameter solenoid having 1000 loops.
(b) How much energy is stored in this inductor when 20.0 A of current flows through it?
(c) How fast can it be turned off if the induced emf cannot exceed 3.00 V?
93. A precision laboratory resistor is made of a coil of wire 1.50 cm in diameter and 4.00 cm long, and it has 500 turns.
(a) What is its self-inductance?
(b) What average emf is induced if the 12.0 A current through it is turned on in 5.00 ms (one-fourth of a cycle for 50 Hz AC)?
(c) What is its inductance if it is shortened to half its length and counter-wound (two layers of 250 turns in opposite directions)?
Solution
(a) 1.39 mH
(b) 3.33 V
(c) Zero
94. The heating coils in a hair dryer are 0.800 cm in diameter, have a combined length of 1.00 m, and a total of 400 turns.
(a) What is their total self-inductance assuming they act like a single solenoid?
(b) How much energy is stored in them when 6.00 A flows?
(c) What average emf opposes shutting them off if this is done in 5.00 ms (one-fourth of a cycle for 50 Hz AC)?
95. When the 20.0 A current through an inductor is turned off in 1.50 ms, an 800 V emf is induced, opposing the change. What is the value of the self-inductance?
Solution
60.0 mH
96. How fast can the 150 A current through a 0.250 H inductor be shut off if the induced emf cannot exceed 75.0 V?
97. Integrated Concepts
A very large, superconducting solenoid such as one used in MRI scans, stores 1.00 MJ of energy in its magnetic field when 100 A flows.
(a) Find its self-inductance.
(b) If the coils “go normal,” they gain resistance and start to dissipate thermal energy. What temperature increase is produced if all the stored energy goes into heating the 1000 kg magnet, given its average specific heat is \displaystyle 200 J/kg⋅ºC?
Solution
(a) 200 H
(b) 5.00ºC
98. Unreasonable Results
A 25.0 H inductor has 100 A of current turned off in 1.00 ms.
(a) What voltage is induced to oppose this?
(b) What is unreasonable about this result?
(c) Which assumption or premise is responsible?
23.10 RL Circuits
99. If you want a characteristic \displaystyle RL time constant of 1.00 s, and you have a 500 Ω resistor, what value of self-inductance is needed?
Solution
500 H
100. Your \displaystyle RL circuit has a characteristic time constant of 20.0 ns, and a resistance of \displaystyle 5.00 MΩ.
(a) What is the inductance of the circuit?
(b) What resistance would give you a 1.00 ns time constant, perhaps needed for quick response in an oscilloscope?
101. A large superconducting magnet, used for magnetic resonance imaging, has a 50.0 H inductance. If you want current through it to be adjustable with a 1.00 s characteristic time constant, what is the minimum resistance of system?
Solution
50.0 Ω
102. Verify that after a time of 10.0 ms, the current for the situation considered in Example will be 0.183 A as stated.
103. Suppose you have a supply of inductors ranging from 1.00 nH to 10.0 H, and resistors ranging from \displaystyle 0.100Ω to \displaystyle 1.00MΩ. What is the range of characteristic \displaystyle RL time constants you can produce by connecting a single resistor to a single inductor?
Solution
\displaystyle 1.00×10^{–18}s to 0.100 s
104. (a) What is the characteristic time constant of a 25.0 mH inductor that has a resistance of \displaystyle 4.00Ω?
(b) If it is connected to a 12.0 V battery, what is the current after 12.5 ms?
105. What percentage of the final current \displaystyle I_0 flows through an inductor \displaystyle L in series with a resistor \displaystyle R, three time constants after the circuit is completed?
Solution
95.0%
106. The 5.00 A current through a 1.50 H inductor is dissipated by a \displaystyle 2.00 Ω resistor in a circuit like that in Figure with the switch in position 2.
(a) What is the initial energy in the inductor?
(b) How long will it take the current to decline to 5.00% of its initial value?
(c) Calculate the average power dissipated, and compare it with the initial power dissipated by the resistor.
107. (a) Use the exact exponential treatment to find how much time is required to bring the current through an 80.0 mH inductor in series with a \displaystyle 15.0 Ω resistor to 99.0% of its final value, starting from zero.
(b) Compare your answer to the approximate treatment using integral numbers of τ.
(c) Discuss how significant the difference is.
Solution
(a) 24.6 ms
(b) 26.7 ms
(c) 9% difference, which is greater than the inherent uncertainty in the given parameters.
108. (a) Using the exact exponential treatment, find the time required for the current through a 2.00 H inductor in series with a 0.500 Ω resistor to be reduced to 0.100% of its original value.
(b) Compare your answer to the approximate treatment using integral numbers of \displaystyle τ.
(c) Discuss how significant the difference is.
23.11 Reactance, Inductive and Capacitive
109. At what frequency will a 30.0 mH inductor have a reactance of 100 Ω?
Solution
531 Hz
110. What value of inductance should be used if a \displaystyle 20.0 kΩ reactance is needed at a frequency of 500 Hz?
111. What capacitance should be used to produce a \displaystyle 2.00 MΩ reactance at 60.0 Hz?
Solution
1.33 nF
112. At what frequency will an 80.0 mF capacitor have a reactance of \displaystyle 0.250 Ω?
113. (a) Find the current through a 0.500 H inductor connected to a 60.0 Hz, 480 V AC source.
(b) What would the current be at 100 kHz?
Solution
(a) 2.55 A
(b) 1.53 mA
114. (a) What current flows when a 60.0 Hz, 480 V AC source is connected to a 0.250 μF capacitor?
(b) What would the current be at 25.0 kHz?
115. A 20.0 kHz, 16.0 V source connected to an inductor produces a 2.00 A current. What is the inductance?
Solution
63.7 µH
116. A 20.0 Hz, 16.0 V source produces a 2.00 mA current when connected to a capacitor. What is the capacitance?
117. (a) An inductor designed to filter high-frequency noise from power supplied to a personal computer is placed in series with the computer. What minimum inductance should it have to produce a \displaystyle 2.00 kΩ reactance for 15.0 kHz noise?
(b) What is its reactance at 60.0 Hz?
Solution
(a) 21.2 mH
(b) 8.00 Ω
118. The capacitor in Figure(a) is designed to filter low-frequency signals, impeding their transmission between circuits.
(a) What capacitance is needed to produce a \displaystyle 100 kΩ reactance at a frequency of 120 Hz?
(b) What would its reactance be at 1.00 MHz?
(c) Discuss the implications of your answers to (a) and (b).
119. The capacitor in Figure(b) will filter high-frequency signals by shorting them to earth/ground.
(a) What capacitance is needed to produce a reactance of \displaystyle 10.0 mΩ for a 5.00 kHz signal?
(b) What would its reactance be at 3.00 Hz? (c) Discuss the implications of your answers to (a) and (b).
Solution
(a) 3.18 mF
(b) 16.7 Ω
120. Unreasonable Results
In a recording of voltages due to brain activity (an EEG), a 10.0 mV signal with a 0.500 Hz frequency is applied to a capacitor, producing a current of 100 mA. Resistance is negligible.
(a) What is the capacitance?
(b) What is unreasonable about this result?
(c) Which assumption or premise is responsible?
121. Construct Your Own Problem
Consider the use of an inductor in series with a computer operating on 60 Hz electricity. Construct a problem in which you calculate the relative reduction in voltage of incoming high frequency noise compared to 60 Hz voltage. Among the things to consider are the acceptable series reactance of the inductor for 60 Hz power and the likely frequencies of noise coming through the power lines.
23.12 RLC Series AC Circuits
122. An \displaystyle RL circuit consists of a \displaystyle 40.0 Ω resistor and a 3.00 mH inductor.
(a) Find its impedance \displaystyle Z at 60.0 Hz and 10.0 kHz.
(b) Compare these values of \displaystyle Z with those found in Example in which there was also a capacitor.
Solution
(a) \displaystyle 40.02 Ω at 60.0 Hz, \displaystyle 193 Ω at 10.0 kHz
(b) At 60 Hz, with a capacitor, \displaystyle Z=531 Ω, over 13 times as high as without the capacitor. The capacitor makes a large difference at low frequencies. At 10 kHz, with a capacitor \displaystyle Z=190 Ω, about the same as without the capacitor. The capacitor has a smaller effect at high frequencies.
123. An \displaystyle RC circuit consists of a \displaystyle 40.0 Ω resistor and a \displaystyle 5.00 μF capacitor.
(a) Find its impedance at 60.0 Hz and 10.0 kHz.
(b) Compare these values of \displaystyle Z with those found in Example, in which there was also an inductor.
124. An \displaystyle C circuit consists of a \displaystyle 3.00mH inductor and a \displaystyle 5.00μF capacitor.
(a) Find its impedance at 60.0 Hz and 10.0 kHz.
(b) Compare these values of \displaystyle Z with those found in Example in which there was also a resistor.
Solution
(a) \displaystyle 529 Ω at 60.0 Hz, \displaystyle 185 Ω at 10.0 kHz
(b) These values are close to those obtained in Example because at low frequency the capacitor dominates and at high frequency the inductor dominates. So in both cases the resistor makes little contribution to the total impedance.
125. What is the resonant frequency of a 0.500 mH inductor connected to a \displaystyle 40.0 μF capacitor?
126. To receive AM radio, you want an \displaystyle RLC circuit that can be made to resonate at any frequency between 500 and 1650 kHz. This is accomplished with a fixed \displaystyle 1.00 μH inductor connected to a variable capacitor. What range of capacitance is needed?
Solution
9.30 nF to 101 nF
127. Suppose you have a supply of inductors ranging from 1.00 nH to 10.0 H, and capacitors ranging from 1.00 pF to 0.100 F. What is the range of resonant frequencies that can be achieved from combinations of a single inductor and a single capacitor?
128. What capacitance do you need to produce a resonant frequency of 1.00 GHz, when using an 8.00 nH inductor?
Solution
3.17 pF
129. What inductance do you need to produce a resonant frequency of 60.0 Hz, when using a \displaystyle 2.00 μF capacitor?
130. The lowest frequency in the FM radio band is 88.0 MHz.
(a) What inductance is needed to produce this resonant frequency if it is connected to a 2.50 pF capacitor?
(b) The capacitor is variable, to allow the resonant frequency to be adjusted to as high as 108 MHz. What must the capacitance be at this frequency?
Solution
(a) \displaystyle 1.31 μH
(b) \displaystyle 1.66 pF
131. An \displaystyle RLC series circuit has a \displaystyle 2.50 Ω resistor, a \displaystyle 100 μH inductor, and an \displaystyle 80.0 μF capacitor.
(a) Find the circuit’s impedance at 120 Hz.
(b) Find the circuit’s impedance at 5.00 kHz.
(c) If the voltage source has \displaystyle V_{rms}=5.60V, what is \displaystyle I_{rms} at each frequency?
(d) What is the resonant frequency of the circuit?
(e) What is \displaystyle I_{rms} at resonance?
132. An \displaystyle RLC series circuit has a \displaystyle 1.00 kΩ resistor, a \displaystyle 150 μH inductor, and a 25.0 nF capacitor.
(a) Find the circuit’s impedance at 500 Hz.
(b) Find the circuit’s impedance at 7.50 kHz.
(c) If the voltage source has \displaystyle V_{rms}=408V, what is \displaystyle I_{rms} at each frequency?
(d) What is the resonant frequency of the circuit?
(e) What is \displaystyle I_{rms} at resonance?
Solution
(a) 12.8 kΩ
(b) 1.31 kΩ
(c) 31.9 mA at 500 Hz, 312 mA at 7.50 kHz
(d) 82.2 kHz
(e) 0.408 A
133. An \displaystyle RLC series circuit has a \displaystyle 2.50 Ω resistor, a \displaystyle 100 μH inductor, and an \displaystyle 80.0 μF capacitor.
(a) Find the power factor at f=120 Hz.
(b) What is the phase angle at 120 Hz?
(c) What is the average power at 120 Hz?
(d) Find the average power at the circuit’s resonant frequency.
134. An \displaystyle RLC series circuit has a \displaystyle 1.00 kΩ resistor, a \displaystyle 150 μH inductor, and a 25.0 nF capacitor
(a) Find the power factor at f=7.50 Hz.
(b) What is the phase angle at this frequency?
(c) What is the average power at this frequency?
(d) Find the average power at the circuit’s resonant frequency.
Solution
(a) 0.159
(b) 80.9º
(c) 26.4 W
(d) 166 W
135. An \displaystyle RLC series circuit has a \displaystyle 200 Ω resistor and a 25.0 mH inductor. At 8000 Hz, the phase angle is \displaystyle 45.0º.
(a) What is the impedance?
(b) Find the circuit’s capacitance.
(c) If \displaystyle V_{rms}=408V is applied, what is the average power supplied?
136. Referring to Example, find the average power at 10.0 kHz.
Solution
16.0 W
Contributors and Attributions
Paul Peter Urone (Professor Emeritus at California State University, Sacramento) and Roger Hinrichs (State University of New York, College at Oswego) with Contributing Authors: Kim Dirks (University of Auckland) and Manjula Sharma (University of Sydney). This work is licensed by OpenStax University Physics under a Creative Commons Attribution License (by 4.0).

