23.6: Motional Emf
( \newcommand{\kernel}{\mathrm{null}\,}\)
Learning Objectives
By the end of this section, you will be able to:
- Calculate emf, force, magnetic field, and work due to the motion of an object in a magnetic field.
As we have seen, any change in magnetic flux induces an emf opposing that change—a process known as induction. Motion is one of the major causes of induction. For example, a magnet moved toward a coil induces an emf, and a coil moved toward a magnet produces a similar emf. In this section, we concentrate on motion in a magnetic field that is stationary relative to the Earth, producing what is loosely called motional emf.
One situation where motional emf occurs is known as the Hall effect and has already been examined. Charges moving in a magnetic field experience the magnetic force F=qvBsinθ, which moves opposite charges in opposite directions and produces an emf=Blv. We saw that the Hall effect has applications, including measurements of B and v. We will now see that the Hall effect is one aspect of the broader phenomenon of induction, and we will find that motional emf can be used as a power source.
Consider the situation shown in Figure 23.6.1. A rod is moved at a speed v along a pair of conducting rails separated by a distance l in a uniform magnetic field B. The rails are stationary relative to B and are connected to a stationary resistor R. The resistor could be anything from a light bulb to a voltmeter. Consider the area enclosed by the moving rod, rails, and resistor. B is perpendicular to this area, and the area is increasing as the rod moves. Thus the magnetic flux enclosed by the rails, rod, and resistor is increasing. When flux changes, an emf is induced according to Faraday’s law of induction.
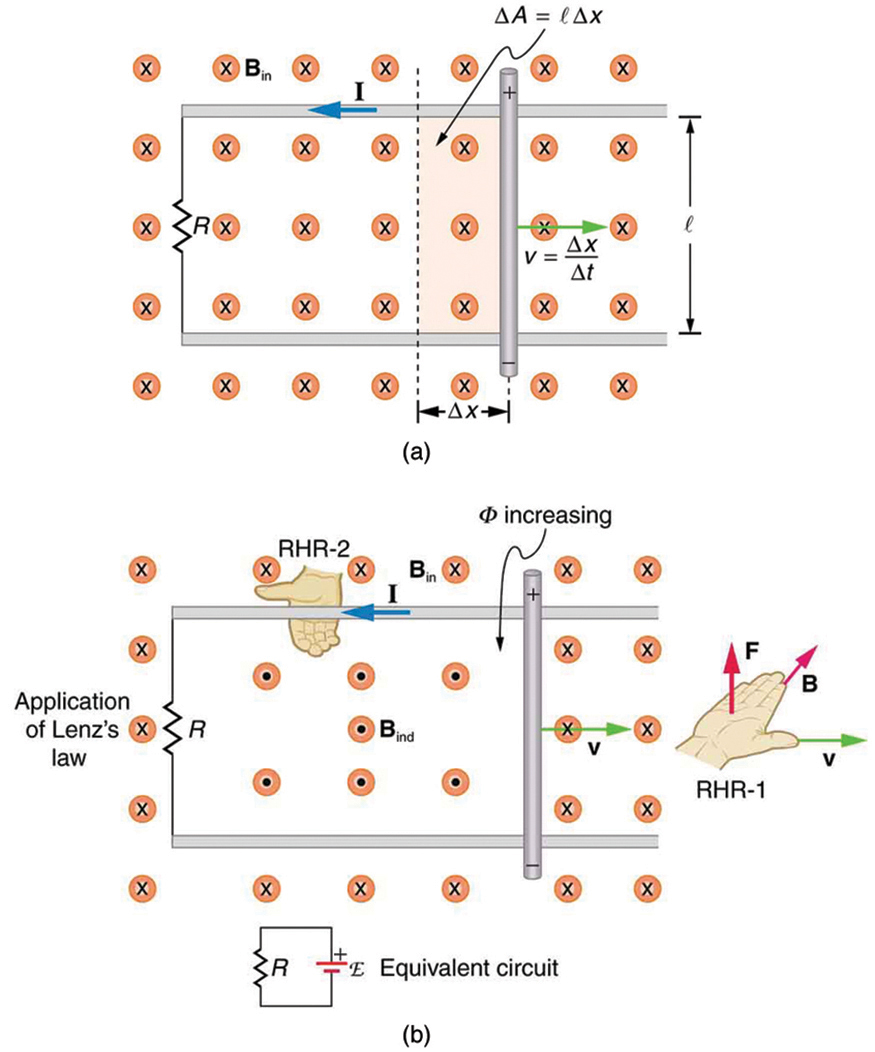
To find the magnitude of emf induced along the moving rod, we use Faraday’s law of induction without the sign:
emf=NΔΦΔt.
Here and below, “emf” implies the magnitude of the emf. In this equation, N=1 and the flux Φ=BAcosθ. We have θ=0∘ and cosθ=1, since B is perpendicular to A. Now ΔΦ=Δ(BA)=BΔA, since B is uniform. Note that the area swept out by the rod is ΔA=lΔx. Entering these quantities into the expression for emf yields
emf=BΔAΔt=BlΔxΔt.
Finally, note that Δx/Δt=v, the velocity of the rod. Entering this into the last expression shows that
emf=Blv(B,l,andvperpendicular)
is the motional emf. This is the same expression given for the Hall effect previously..
MAKING CONNECTIONS: UNIFICATION OF FORCES:
There are many connections between the electric force and the magnetic force. The fact that a moving electric field produces a magnetic field and, conversely, a moving magnetic field produces an electric field is part of why electric and magnetic forces are now considered to be different manifestations of the same force. This classic unification of electric and magnetic forces into what is called the electromagnetic force is the inspiration for contemporary efforts to unify other basic forces.
To find the direction of the induced field, the direction of the current, and the polarity of the induced emf, we apply Lenz’s law as explained in "Faraday's Law of Induction: Lenz's Law" (Figure 23.6.1b).
Flux is increasing, since the area enclosed is increasing. Thus the induced field must oppose the existing one and be out of the page. And so the RHR-2 requires that I be counterclockwise, which in turn means the top of the rod is positive as shown.
Motional emf also occurs if the magnetic field moves and the rod (or other object) is stationary relative to the Earth (or some observer). We have seen an example of this in the situation where a moving magnet induces an emf in a stationary coil. It is the relative motion that is important. What is emerging in these observations is a connection between magnetic and electric fields. A moving magnetic field produces an electric field through its induced emf. We already have seen that a moving electric field produces a magnetic field—moving charge implies moving electric field and moving charge produces a magnetic field.
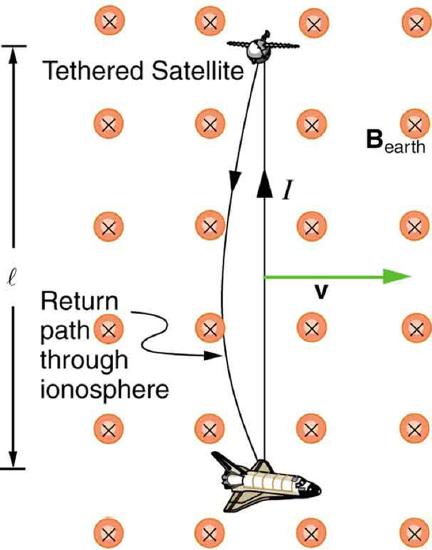
Motional emfs in the Earth’s weak magnetic field are not ordinarily very large, or we would notice voltage along metal rods, such as a screwdriver, during ordinary motions. For example, a simple calculation of the motional emf of a 1 m rod moving at 3.0 m/s perpendicular to the Earth’s field gives emf=Blv=(5.0×10−5T)(1.0m)(3.0m/s)=150μV. This small value is consistent with experience. There is a spectacular exception, however. In 1992 and 1996, attempts were made with the space shuttle to create large motional emfs. The Tethered Satellite was to be let out on a 20 km length of wire as shown in Figure 2, to create a 5 kV emf by moving at orbital speed through the Earth’s field. This emf could be used to convert some of the shuttle’s kinetic and potential energy into electrical energy if a complete circuit could be made. To complete the circuit, the stationary ionosphere was to supply a return path for the current to flow. (The ionosphere is the rarefied and partially ionized atmosphere at orbital altitudes. It conducts because of the ionization. The ionosphere serves the same function as the stationary rails and connecting resistor in Figure 1, without which there would not be a complete circuit.) Drag on the current in the cable due to the magnetic force F=IlBsinθ does the work that reduces the shuttle’s kinetic and potential energy and allows it to be converted to electrical energy. The tests were both unsuccessful. In the first, the cable hung up and could only be extended a couple of hundred meters; in the second, the cable broke when almost fully extended. The example below indicates feasibility in principle.
Example 23.6.1: Calculating the Large Motional Emf of an Object in Orbit
Calculate the motional emf induced along a 20.0 km long conductor moving at an orbital speed of 7.80 km/s perpendicular to the Earth’s 5.00×10−5T magnetic field.
Strategy:
This is a straightforward application of the expression for motional emf--emf=Blv.
Solution:
Entering the given values into emf=Blv gives emf=Blv
Discussion:
The value obtained is greater than the 5 kV measured voltage for the shuttle experiment, since the actual orbital motion of the tether is not perpendicular to the Earth’s field. The 7.80 kV value is the maximum emf obtained when θ=90∘ and sinθ=1.
Summary
- An emf induced by motion relative to a magnetic field B is called a motional emf and is given by emf=Blv(B,l,andvperpendicular),where l is the length of the object moving at speed v relative to the field.


