12.E: Fluid Dynamics and Its Biological and Medical Applications (Exercises)
- Page ID
- 8798
( \newcommand{\kernel}{\mathrm{null}\,}\)
Conceptual Questions
12.1: Flow Rate and Its Relation to Velocity
1. What is the difference between flow rate and fluid velocity? How are they related?
2. Many figures in the text show streamlines. Explain why fluid velocity is greatest where streamlines are closest together. (Hint: Consider the relationship between fluid velocity and the cross-sectional area through which it flows.)
3. Identify some substances that are incompressible and some that are not.
12.2: Bernoulli’s Equation
4. You can squirt water a considerably greater distance by placing your thumb over the end of a garden hose and then releasing, than by leaving it completely uncovered. Explain how this works.
5. Water is shot nearly vertically upward in a decorative fountain and the stream is observed to broaden as it rises. Conversely, a stream of water falling straight down from a faucet narrows. Explain why, and discuss whether surface tension enhances or reduces the effect in each case.
6. Look back to Figure. Answer the following two questions. Why is Po less than atmospheric? Why is Po greater than Pi?
7. Give an example of entrainment not mentioned in the text.
8. Many entrainment devices have a constriction, called a Venturi, such as shown in Figure. How does this bolster entrainment?
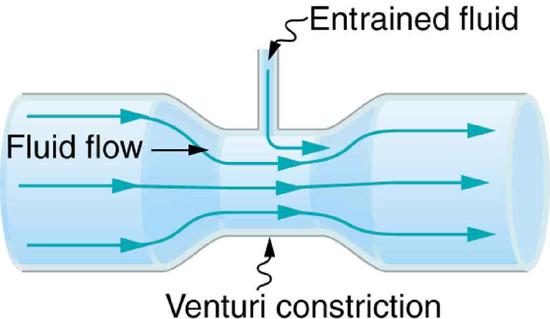
A tube with a narrow segment designed to enhance entrainment is called a Venturi. These are very commonly used in carburetors and aspirators.
9. Some chimney pipes have a T-shape, with a crosspiece on top that helps draw up gases whenever there is even a slight breeze. Explain how this works in terms of Bernoulli’s principle.
10. Is there a limit to the height to which an entrainment device can raise a fluid? Explain your answer.
11. Why is it preferable for airplanes to take off into the wind rather than with the wind?
12. Roofs are sometimes pushed off vertically during a tropical cyclone, and buildings sometimes explode outward when hit by a tornado. Use Bernoulli’s principle to explain these phenomena.
13. Why does a sailboat need a keel?
14. It is dangerous to stand close to railroad tracks when a rapidly moving commuter train passes. Explain why atmospheric pressure would push you toward the moving train.
15. Water pressure inside a hose nozzle can be less than atmospheric pressure due to the Bernoulli effect. Explain in terms of energy how the water can emerge from the nozzle against the opposing atmospheric pressure.
16. A perfume bottle or atomizer sprays a fluid that is in the bottle. (Figure.) How does the fluid rise up in the vertical tube in the bottle?

Atomizer: perfume bottle with tube to carry perfume up through the bottle. (credit: Antonia Foy, Flickr)
17. If you lower the window on a car while moving, an empty plastic bag can sometimes fly out the window. Why does this happen?
12.3: The Most General Applications of Bernoulli’s Equation
18. Based on Bernoulli’s equation, what are three forms of energy in a fluid? (Note that these forms are conservative, unlike heat transfer and other dissipative forms not included in Bernoulli’s equation.)
19. Water that has emerged from a hose into the atmosphere has a gauge pressure of zero. Why? When you put your hand in front of the emerging stream you feel a force, yet the water’s gauge pressure is zero. Explain where the force comes from in terms of energy.
20. The old rubber boot shown in Figure has two leaks. To what maximum height can the water squirt from Leak 1? How does the velocity of water emerging from Leak 2 differ from that of leak 1? Explain your responses in terms of energy.
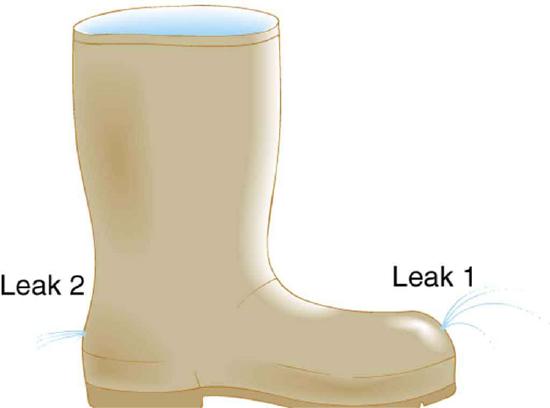
Water emerges from two leaks in an old boot.
21. Water pressure inside a hose nozzle can be less than atmospheric pressure due to the Bernoulli effect. Explain in terms of energy how the water can emerge from the nozzle against the opposing atmospheric pressure.
12.4: Viscosity and Laminar Flow; Poiseuille’s Law
22. Explain why the viscosity of a liquid decreases with temperature—that is, how might increased temperature reduce the effects of cohesive forces in a liquid? Also explain why the viscosity of a gas increases with temperature—that is, how does increased gas temperature create more collisions between atoms and molecules?
23. When paddling a canoe upstream, it is wisest to travel as near to the shore as possible. When canoeing downstream, it may be best to stay near the middle. Explain why.
24. Why does flow decrease in your shower when someone flushes the toilet?
25. Plumbing usually includes air-filled tubes near water faucets, as shown in Figure. Explain why they are needed and how they work.
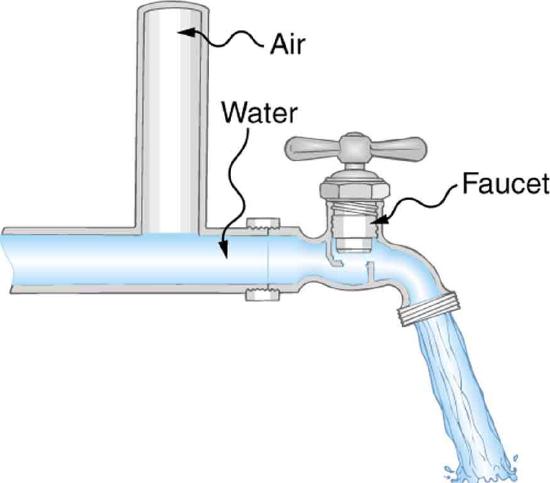
The vertical tube near the water tap remains full of air and serves a useful purpose.
12.5: The Onset of Turbulence
26. Doppler ultrasound can be used to measure the speed of blood in the body. If there is a partial constriction of an artery, where would you expect blood speed to be greatest, at or nearby the constriction? What are the two distinct causes of higher resistance in the constriction?
27. Sink drains often have a device such as that shown in Figure to help speed the flow of water. How does this work?
You will find devices such as this in many drains. They significantly increase flow rate.
28. Some ceiling fans have decorative wicker reeds on their blades. Discuss whether these fans are as quiet and efficient as those with smooth blades.
12.6: Motion of an Object in a Viscous Fluid
29. What direction will a helium balloon move inside a car that is slowing down—toward the front or back? Explain your answer.
30. Will identical raindrops fall more rapidly in 5º C air or 25º C air, neglecting any differences in air density? Explain your answer.
31. If you took two marbles of different sizes, what would you expect to observe about the relative magnitudes of their terminal velocities?
12.7: Molecular Transport Phenomena: Diffusion, Osmosis, and Related Processes
32. Why would you expect the rate of diffusion to increase with temperature? Can you give an example, such as the fact that you can dissolve sugar more rapidly in hot water?
33. How are osmosis and dialysis similar? How do they differ?
Problem & Exercises
12.1: Flow Rate and Its Relation to Velocity
34. What is the average flow rate in cm3/s of gasoline to the engine of a car traveling at 100 km/h if it averages 10.0 km/L?
Solution
2.78cm3/s
35. The heart of a resting adult pumps blood at a rate of 5.00 L/min.
(a) Convert this to cm3/s.
(b) What is this rate in m3/s?
36. Blood is pumped from the heart at a rate of 5.0 L/min into the aorta (of radius 1.0 cm). Determine the speed of blood through the aorta.
Solution
27 cm/s
37. Blood is flowing through an artery of radius 2 mm at a rate of 40 cm/s. Determine the flow rate and the volume that passes through the artery in a period of 30 s.
38. The Huka Falls on the Waikato River is one of New Zealand’s most visited natural tourist attractions (see Figure). On average the river has a flow rate of about 300,000 L/s. At the gorge, the river narrows to 20 m wide and averages 20 m deep.
(a) What is the average speed of the river in the gorge?
(b) What is the average speed of the water in the river downstream of the falls when it widens to 60 m and its depth increases to an average of 40 m?

The Huka Falls in Taupo, New Zealand, demonstrate flow rate. (credit: RaviGogna, Flickr
Solution
(a) 0.75 m/s
(b) 0.13 m/s
39. A major artery with a cross-sectional area of 1.00cm2 branches into 18 smaller arteries, each with an average cross-sectional area of 0.400cm2. By what factor is the average velocity of the blood reduced when it passes into these branches?
40. (a) As blood passes through the capillary bed in an organ, the capillaries join to form venules (small veins). If the blood speed increases by a factor of 4.00 and the total cross-sectional area of the venules is 10.0cm2, what is the total cross-sectional area of the capillaries feeding these venules?
(b) How many capillaries are involved if their average diameter is 10.0μm?
Solution
(a) 40.0cm2
(b) 5.09×107
41. The human circulation system has approximately 1×109 capillary vessels. Each vessel has a diameter of about 8μm. Assuming cardiac output is 5 L/min, determine the average velocity of blood flow through each capillary vessel.
42. (a) Estimate the time it would take to fill a private swimming pool with a capacity of 80,000 L using a garden hose delivering 60 L/min.
(b) How long would it take to fill if you could divert a moderate size river, flowing at 5000m3/s, into it?
Solution
(a) 22 h
(b) 0.016 s
43. The flow rate of blood through a \displaystyle 2.00×10^{–6}-m -radius capillary is \displaystyle 3.80×10^{-9}cm^3/s.
(a) What is the speed of the blood flow? (This small speed allows time for diffusion of materials to and from the blood.)
(b) Assuming all the blood in the body passes through capillaries, how many of them must there be to carry a total flow of 90.0cm3/s? (The large number obtained is an overestimate, but it is still reasonable.)
44. (a) What is the fluid speed in a fire hose with a 9.00-cm diameter carrying 80.0 L of water per second? (b) What is the flow rate in cubic meters per second? (c) Would your answers be different if salt water replaced the fresh water in the fire hose?
Solution
(a) 12.6 m/s
(b) \displaystyle 0.0800m^3/s
(c) No, independent of density.
45. The main uptake air duct of a forced air gas heater is 0.300 m in diameter. What is the average speed of air in the duct if it carries a volume equal to that of the house’s interior every 15 min? The inside volume of the house is equivalent to a rectangular solid 13.0 m wide by 20.0 m long by 2.75 m high.
46. Water is moving at a velocity of 2.00 m/s through a hose with an internal diameter of 1.60 cm.
(a) What is the flow rate in liters per second?
(b) The fluid velocity in this hose’s nozzle is 15.0 m/s. What is the nozzle’s inside diameter?
Solution
(a) 0.402 L/s
(b) 0.584 cm
47. Prove that the speed of an incompressible fluid through a constriction, such as in a Venturi tube, increases by a factor equal to the square of the factor by which the diameter decreases. (The converse applies for flow out of a constriction into a larger-diameter region.)
48. Water emerges straight down from a faucet with a 1.80-cm diameter at a speed of 0.500 m/s. (Because of the construction of the faucet, there is no variation in speed across the stream.)
(a) What is the flow rate in \displaystyle cm^3/s?
(b) What is the diameter of the stream 0.200 m below the faucet? Neglect any effects due to surface tension.
Solution
(a) \displaystyle 127cm^3/s
(b) 0.890 cm
49. Unreasonable Results
A mountain stream is 10.0 m wide and averages 2.00 m in depth. During the spring runoff, the flow in the stream reaches \displaystyle 100,000m^3/s.
(a) What is the average velocity of the stream under these conditions?
(b) What is unreasonable about this velocity?
(c) What is unreasonable or inconsistent about the premises?
12.2: Bernoulli’s Equation
50. Verify that pressure has units of energy per unit volume.
Solution
\displaystyle P=\frac{Force}{Area},
\displaystyle (P)_{units}=N/m^2=N⋅m/m^3=J/m^3
\displaystyle =energy/volume
51. Suppose you have a wind speed gauge like the pitot tube shown in [link](b). By what factor must wind speed increase to double the value of \displaystyle h in the manometer? Is this independent of the moving fluid and the fluid in the manometer?
52. If the pressure reading of your pitot tube is 15.0 mm Hg at a speed of 200 km/h, what will it be at 700 km/h at the same altitude?
Solution
184 mm Hg
53. Calculate the maximum height to which water could be squirted with the hose in [link] example if it: (a) Emerges from the nozzle. (b) Emerges with the nozzle removed, assuming the same flow rate.
54. Every few years, winds in Boulder, Colorado, attain sustained speeds of 45.0 m/s (about 100 mi/h) when the jet stream descends during early spring. Approximately what is the force due to the Bernoulli effect on a roof having an area of \displaystyle 220m^2? Typical air density in Boulder is \displaystyle 1.14kg/m^3, and the corresponding atmospheric pressure is \displaystyle 8.89×10^4N/m^2. (Bernoulli’s principle as stated in the text assumes laminar flow. Using the principle here produces only an approximate result, because there is significant turbulence.)
Solution
\displaystyle 2.54×10^5N
55. a) Calculate the approximate force on a square meter of sail, given the horizontal velocity of the wind is 6.00 m/s parallel to its front surface and 3.50 m/s along its back surface. Take the density of air to be \displaystyle 1.29 kg/m^3. (The calculation, based on Bernoulli’s principle, is approximate due to the effects of turbulence.)
(b) Discuss whether this force is great enough to be effective for propelling a sailboat.
56. (a) What is the pressure drop due to the Bernoulli effect as water goes into a 3.00-cm-diameter nozzle from a 9.00-cm-diameter fire hose while carrying a flow of 40.0 L/s?
(b) To what maximum height above the nozzle can this water rise? (The actual height will be significantly smaller due to air resistance.)
Solution
(a) \displaystyle 1.58×10^6N/m^2
(b) 163 m
57. (a) Using Bernoulli’s equation, show that the measured fluid speed v for a pitot tube, like the one in Figure(b), is given by
\displaystyle v=(\frac{2ρ′gh}{ρ})^{1/2},
where \displaystyle h is the height of the manometer fluid, \displaystyle ρ′ is the density of the manometer fluid, \displaystyle ρ\(\displaystyle is the density of the moving fluid, and \(\displaystyle g\(\displaystyle is the acceleration due to gravity. (Note that v is indeed proportional to the square root of \(\displaystyle h, as stated in the text.)
(b) Calculate \displaystyle v for moving air if a mercury manometer’s \displaystyle h is 0.200 m.
12.3: The Most General Applications of Bernoulli’s Equation
58. Hoover Dam on the Colorado River is the highest dam in the United States at 221 m, with an output of 1300 MW. The dam generates electricity with water taken from a depth of 150 m and an average flow rate of \displaystyle 650m^3/s.
(a) Calculate the power in this flow.
(b) What is the ratio of this power to the facility’s average of 680 MW?
Solution
(a) \displaystyle 9.56×10^8W
(b) 1.4
59. A frequently quoted rule of thumb in aircraft design is that wings should produce about 1000 N of lift per square meter of wing. (The fact that a wing has a top and bottom surface does not double its area.)
(a) At takeoff, an aircraft travels at 60.0 m/s, so that the air speed relative to the bottom of the wing is 60.0 m/s. Given the sea level density of air to be \displaystyle 1.29kg/m^3, how fast must it move over the upper surface to create the ideal lift?
(b) How fast must air move over the upper surface at a cruising speed of 245 m/s and at an altitude where air density is one-fourth that at sea level? (Note that this is not all of the aircraft’s lift—some comes from the body of the plane, some from engine thrust, and so on. Furthermore, Bernoulli’s principle gives an approximate answer because flow over the wing creates turbulence.)
60. The left ventricle of a resting adult’s heart pumps blood at a flow rate of \displaystyle 83.0cm^3/s, increasing its pressure by 110 mm Hg, its speed from zero to 30.0 cm/s, and its height by 5.00 cm. (All numbers are averaged over the entire heartbeat.) Calculate the total power output of the left ventricle. Note that most of the power is used to increase blood pressure.
Solution
1.26 W
61. A sump pump (used to drain water from the basement of houses built below the water table) is draining a flooded basement at the rate of 0.750 L/s, with an output pressure of \displaystyle 3.00×10^5N/m^2.
(a) The water enters a hose with a 3.00-cm inside diameter and rises 2.50 m above the pump. What is its pressure at this point?
(b) The hose goes over the foundation wall, losing 0.500 m in height, and widens to 4.00 cm in diameter. What is the pressure now? You may neglect frictional losses in both parts of the problem.
12.4: Viscosity and Laminar Flow; Poiseuille’s Law
62. (a) Calculate the retarding force due to the viscosity of the air layer between a cart and a level air track given the following information—air temperature is 20º C, the cart is moving at 0.400 m/s, its surface area is \displaystyle 2.50×10^{−2}m^2, and the thickness of the air layer is \displaystyle 6.00×10^{−5}m.
(b) What is the ratio of this force to the weight of the 0.300-kg cart?
Solution
(a) \displaystyle 3.02×10^{−3}N
(b) \displaystyle 1.03×10^{−3}
63. What force is needed to pull one microscope slide over another at a speed of 1.00 cm/s, if there is a 0.500-mm-thick layer of 20º C water between them and the contact area is \displaystyle 8.00cm^2?
64. A glucose solution being administered with an IV has a flow rate of \displaystyle 4.00cm^3/min. What will the new flow rate be if the glucose is replaced by whole blood having the same density but a viscosity 2.50 times that of the glucose? All other factors remain constant.
Solution
\displaystyle 1.60 cm^3/min
65. The pressure drop along a length of artery is 100 Pa, the radius is 10 mm, and the flow is laminar. The average speed of the blood is 15 mm/s.
(a) What is the net force on the blood in this section of artery?
(b) What is the power expended maintaining the flow?
66. A small artery has a length of \displaystyle 1.1×10^{−3}m and a radius of \displaystyle 2.5×10^{−5}m. If the pressure drop across the artery is 1.3 kPa, what is the flow rate through the artery? (Assume that the temperature is 37º C.)
Solution
\displaystyle 8.7×10^{−11}m^3/s
67. Fluid originally flows through a tube at a rate of \displaystyle 100cm^3/s. To illustrate the sensitivity of flow rate to various factors, calculate the new flow rate for the following changes with all other factors remaining the same as in the original conditions.
(a) Pressure difference increases by a factor of 1.50.
(b) A new fluid with 3.00 times greater viscosity is substituted.
(c) The tube is replaced by one having 4.00 times the length.
(d) Another tube is used with a radius 0.100 times the original.
(e) Yet another tube is substituted with a radius 0.100 times the original and half the length, and the pressure difference is increased by a factor of 1.50.
68. The arterioles (small arteries) leading to an organ, constrict in order to decrease flow to the organ. To shut down an organ, blood flow is reduced naturally to 1.00% of its original value. By what factor did the radii of the arterioles constrict? Penguins do this when they stand on ice to reduce the blood flow to their feet.
Solution
0.316
69. Angioplasty is a technique in which arteries partially blocked with plaque are dilated to increase blood flow. By what factor must the radius of an artery be increased in order to increase blood flow by a factor of 10?
70. (a) Suppose a blood vessel’s radius is decreased to 90.0% of its original value by plaque deposits and the body compensates by increasing the pressure difference along the vessel to keep the flow rate constant. By what factor must the pressure difference increase?
(b) If turbulence is created by the obstruction, what additional effect would it have on the flow rate?
Solution
(a) 1.52
(b) Turbulence will decrease the flow rate of the blood, which would require an even larger increase in the pressure difference, leading to higher blood pressure.
71. A spherical particle falling at a terminal speed in a liquid must have the gravitational force balanced by the drag force and the buoyant force. The buoyant force is equal to the weight of the displaced fluid, while the drag force is assumed to be given by Stokes Law, \displaystyle F_s=6πrηv. Show that the terminal speed is given by
\displaystyle v=\frac{2R^2g}{9η}(ρ_s−ρ_1),
where \displaystyle R is the radius of the sphere, \displaystyle ρ_s is its density, and \displaystyle ρ_1 is the density of the fluid and \displaystyle η the coefficient of viscosity.
72. Using the equation of the previous problem, find the viscosity of motor oil in which a steel ball of radius 0.8 mm falls with a terminal speed of 4.32 cm/s. The densities of the ball and the oil are 7.86 and 0.88 g/mL, respectively.
Solution
\displaystyle 225mPa⋅s
73. A skydiver will reach a terminal velocity when the air drag equals their weight. For a skydiver with high speed and a large body, turbulence is a factor. The drag force then is approximately proportional to the square of the velocity. Taking the drag force to be \displaystyle F_D=\frac{1}{2}ρAv^2 and setting this equal to the person’s weight, find the terminal speed for a person falling “spread eagle.” Find both a formula and a number for \displaystyle v_t, with assumptions as to size.
74. A layer of oil 1.50 mm thick is placed between two microscope slides. Researchers find that a force of \displaystyle 5.50×10^{−4}N is required to glide one over the other at a speed of 1.00 cm/s when their contact area is \displaystyle 6.00cm^2. What is the oil’s viscosity? What type of oil might it be?
Solution
\displaystyle 0.138 Pa⋅s or Olive oil.
75. (a) Verify that a 19.0% decrease in laminar flow through a tube is caused by a 5.00% decrease in radius, assuming that all other factors remain constant, as stated in the text.
(b) What increase in flow is obtained from a 5.00% increase in radius, again assuming all other factors remain constant?
76. Example dealt with the flow of saline solution in an IV system.
(a) Verify that a pressure of \displaystyle 1.62×10^4N/m^2 is created at a depth of 1.61 m in a saline solution, assuming its density to be that of sea water.
(b) Calculate the new flow rate if the height of the saline solution is decreased to 1.50 m.
(c) At what height would the direction of flow be reversed? (This reversal can be a problem when patients stand up.)
Solution
(a) \displaystyle 1.62×10^4N/m^2
(b) \displaystyle 0.111 cm^3/s
(c)10.6 cm
77. When physicians diagnose arterial blockages, they quote the reduction in flow rate. If the flow rate in an artery has been reduced to 10.0% of its normal value by a blood clot and the average pressure difference has increased by 20.0%, by what factor has the clot reduced the radius of the artery?
78. During a marathon race, a runner’s blood flow increases to 10.0 times her resting rate. Her blood’s viscosity has dropped to 95.0% of its normal value, and the blood pressure difference across the circulatory system has increased by 50.0%. By what factor has the average radii of her blood vessels increased?
Solution
1.59
79. Water supplied to a house by a water main has a pressure of \displaystyle 3.00×10^5N/m^2 early on a summer day when neighborhood use is low. This pressure produces a flow of 20.0 L/min through a garden hose. Later in the day, pressure at the exit of the water main and entrance to the house drops, and a flow of only 8.00 L/min is obtained through the same hose.
(a) What pressure is now being supplied to the house, assuming resistance is constant?
(b) By what factor did the flow rate in the water main increase in order to cause this decrease in delivered pressure? The pressure at the entrance of the water main is \displaystyle 5.00×10^5N/m^2, and the original flow rate was 200 L/min.
(c) How many more users are there, assuming each would consume 20.0 L/min in the morning?
80. An oil gusher shoots crude oil 25.0 m into the air through a pipe with a 0.100-m diameter. Neglecting air resistance but not the resistance of the pipe, and assuming laminar flow, calculate the gauge pressure at the entrance of the 50.0-m-long vertical pipe. Take the density of the oil to be \displaystyle 900kg/m^3 and its viscosity to be \displaystyle 1.00(N/m^2)⋅s (or \displaystyle 1.00Pa⋅s). Note that you must take into account the pressure due to the 50.0-m column of oil in the pipe.
Solution
\displaystyle 2.95×10^6N/m^2(gauge pressure)
81. Concrete is pumped from a cement mixer to the place it is being laid, instead of being carried in wheelbarrows. The flow rate is 200.0 L/min through a 50.0-m-long, 8.00-cm-diameter hose, and the pressure at the pump is \displaystyle 8.00×10^6N/m^2.
(a) Calculate the resistance of the hose.
(b) What is the viscosity of the concrete, assuming the flow is laminar?
(c) How much power is being supplied, assuming the point of use is at the same level as the pump? You may neglect the power supplied to increase the concrete’s velocity.
82. Construct Your Own Problem
Consider a coronary artery constricted by arteriosclerosis. Construct a problem in which you calculate the amount by which the diameter of the artery is decreased, based on an assessment of the decrease in flow rate.
83. Consider a river that spreads out in a delta region on its way to the sea. Construct a problem in which you calculate the average speed at which water moves in the delta region, based on the speed at which it was moving up river. Among the things to consider are the size and flow rate of the river before it spreads out and its size once it has spread out. You can construct the problem for the river spreading out into one large river or into multiple smaller rivers.
12.5: The Onset of Turbulence
84. Verify that the flow of oil is laminar (barely) for an oil gusher that shoots crude oil 25.0 m into the air through a pipe with a 0.100-m diameter. The vertical pipe is 50 m long. Take the density of the oil to be \displaystyle 900 kg/m^3 and its viscosity to be \displaystyle 1.00(N/m^2)⋅s (or \displaystyle 1.00 Pa⋅s).
Solution
\displaystyle N_R=1.99×10^2< 2000
85. Show that the Reynolds number \displaystyle N_R is unitless by substituting units for all the quantities in its definition and cancelling.
86. Calculate the Reynolds numbers for the flow of water through
(a) a nozzle with a radius of 0.250 cm and
(b) a garden hose with a radius of 0.900 cm, when the nozzle is attached to the hose. The flow rate through hose and nozzle is 0.500 L/s. Can the flow in either possibly be laminar?
Solution
(a) nozzle: \displaystyle 1.27×10^5, not laminar
(b) hose: \displaystyle 3.51×10^4, not laminar.
87. A fire hose has an inside diameter of 6.40 cm. Suppose such a hose carries a flow of 40.0 L/s starting at a gauge pressure of \displaystyle 1.62×10^6N/m^2. The hose goes 10.0 m up a ladder to a nozzle having an inside diameter of 3.00 cm. Calculate the Reynolds numbers for flow in the fire hose and nozzle to show that the flow in each must be turbulent.
88. Concrete is pumped from a cement mixer to the place it is being laid, instead of being carried in wheelbarrows. The flow rate is 200.0 L/min through a 50.0-m-long, 8.00-cm-diameter hose, and the pressure at the pump is \displaystyle 8.00×10^6N/m^2. Verify that the flow of concrete is laminar taking concrete’s viscosity to be \displaystyle 48.0(N/m^2)⋅s, and given its density is \displaystyle 2300 kg/m^3.
Solution
2.54 << 2000, laminar.
89. At what flow rate might turbulence begin to develop in a water main with a 0.200-m diameter? Assume a \displaystyle 20º C temperature.
90. What is the greatest average speed of blood flow at \displaystyle 37º C in an artery of radius 2.00 mm if the flow is to remain laminar? What is the corresponding flow rate? Take the density of blood to be \displaystyle 1025 kg/m^3.
Solution
1.02 m/s
\displaystyle 1.28×10^{–2}L/s
91. In Take-Home Experiment: Inhalation, we measured the average flow rate \displaystyle Q of air traveling through the trachea during each inhalation. Now calculate the average air speed in meters per second through your trachea during each inhalation. The radius of the trachea in adult humans is approximately \displaystyle 10^{−2}m. From the data above, calculate the Reynolds number for the air flow in the trachea during inhalation. Do you expect the air flow to be laminar or turbulent?
92. Gasoline is piped underground from refineries to major users. The flow rate is \displaystyle 3.00×10^{–2}m^3/s (about 500 gal/min), the viscosity of gasoline is \displaystyle 1.00×10^{–3}(N/m^2)⋅s, and its density is \displaystyle 680kg/m^3.
(a) What minimum diameter must the pipe have if the Reynolds number is to be less than 2000?
(b) What pressure difference must be maintained along each kilometer of the pipe to maintain this flow rate?
Solution
(a) \displaystyle ≥ 13.0 m
(b) \displaystyle 2.68×10^{−6}N/m^2
93. Assuming that blood is an ideal fluid, calculate the critical flow rate at which turbulence is a certainty in the aorta. Take the diameter of the aorta to be 2.50 cm. (Turbulence will actually occur at lower average flow rates, because blood is not an ideal fluid. Furthermore, since blood flow pulses, turbulence may occur during only the high-velocity part of each heartbeat.)
94. Unreasonable Results
A fairly large garden hose has an internal radius of 0.600 cm and a length of 23.0 m. The nozzleless horizontal hose is attached to a faucet, and it delivers 50.0 L/s.
(a) What water pressure is supplied by the faucet?
(b) What is unreasonable about this pressure?
(c) What is unreasonable about the premise?
(d) What is the Reynolds number for the given flow? (Take the viscosity of water as \displaystyle 1.005×10^{–3}(N/m^2)⋅s.)
Solution
(a) 23.7 atm or \displaystyle 344 lb/in^2
(b) The pressure is much too high.
(c) The assumed flow rate is very high for a garden hose.
(d) \displaystyle 5.27×10^6 > > 3000, turbulent, contrary to the assumption of laminar flow when using this equation.
12.7: Molecular Transport Phenomena: Diffusion, Osmosis, and Related Processes
95. You can smell perfume very shortly after opening the bottle. To show that it is not reaching your nose by diffusion, calculate the average distance a perfume molecule moves in one second in air, given its diffusion constant \displaystyle D to be \displaystyle 1.00×10^{–6}m^2/s.
Solution
\displaystyle 1.41×10^{−3}m
96. What is the ratio of the average distances that oxygen will diffuse in a given time in air and water? Why is this distance less in water (equivalently, why is \displaystyle D less in water)?
97. Oxygen reaches the veinless cornea of the eye by diffusing through its tear layer, which is 0.500-mm thick. How long does it take the average oxygen molecule to do this?
Solution
\displaystyle 1.3×10^2s
98. (a) Find the average time required for an oxygen molecule to diffuse through a 0.200-mm-thick tear layer on the cornea.
(b) How much time is required to diffuse \displaystyle 0.500cm^3 of oxygen to the cornea if its surface area is \displaystyle 1.00cm^2?
99. Suppose hydrogen and oxygen are diffusing through air. A small amount of each is released simultaneously. How much time passes before the hydrogen is 1.00 s ahead of the oxygen? Such differences in arrival times are used as an analytical tool in gas chromatography.
Solution
0.391 s
Contributors and Attributions
Paul Peter Urone (Professor Emeritus at California State University, Sacramento) and Roger Hinrichs (State University of New York, College at Oswego) with Contributing Authors: Kim Dirks (University of Auckland) and Manjula Sharma (University of Sydney). This work is licensed by OpenStax University Physics under a Creative Commons Attribution License (by 4.0).


