2.3: Time, Velocity, and Speed

Learning Objectives

By the end of this section, you will be able to:

• Explain the relationships between instantaneous velocity, average velocity, instantaneous speed, average speed, displacement, and time.
• Calculate velocity and speed given initial position, initial time, final position, and final time.
• Derive a graph of velocity vs. time given a graph of position vs. time.
• Interpret a graph of velocity vs. time.

There is more to motion than distance and displacement. Questions such as, “How long does a foot race take?” and “What was the runner’s speed?” cannot be answered without an understanding of other concepts. In this section we add definitions of time, velocity, and speed to expand our description of motion.

Figure \(\PageIndex{1}\): The motion of these racing snails can be described by their speeds and their velocities. (credit: tobitasflickr, Flickr)

Time

As discussed in Physical Quantities and Units, the most fundamental physical quantities are defined by how they are measured. This is the case with time. Every measurement of time involves measuring a change in some physical quantity. It may be a number on a digital clock, a heartbeat, or the position of the Sun in the sky. In physics, the definition of time is simple—time is change, or the interval over which change occurs. It is impossible to know that time has passed unless something changes.

The amount of time or change is calibrated by comparison with a standard. The SI unit for time is the second, abbreviated s. We might, for example, observe that a certain pendulum makes one full swing every 0.75 s. We could then use the pendulum to measure time by counting its swings or, of course, by connecting the pendulum to a clock mechanism that registers time on a dial. This allows us to not only measure the amount of time, but also to determine a sequence of events.

How does time relate to motion? We are usually interested in elapsed time for a particular motion, such as how long it takes an airplane passenger to get from his seat to the back of the plane. To find elapsed time, we note the time at the beginning and end of the motion and subtract the two. For example, a lecture may start at 11:00 A.M. and end at 11:50 A.M., so that the elapsed time would be 50 min. Elapsed time \(Δt\) is the difference between the ending time and beginning time,

\(Δt=t_f−t_0\),

where \(Δt\) is the change in time or elapsed time, \(t_f\) is the time at the end of the motion, and \(t_0\) is the time at the beginning of the motion. (As usual, the delta symbol, \(Δ\), means the change in the quantity that follows it.)

Life is simpler if the beginning time \(t_0\) is taken to be zero, as when we use a stopwatch. If we were using a stopwatch, it would simply read zero at the start of the lecture and 50 min at the end. If \(t_0=0\), then

\[Δt=t_f≡t.\]

In this text, for simplicity’s sake,

• motion starts at time equal to zero (\(t_0=0\))
• the symbol \(t\) is used for elapsed time unless otherwise specified (\(Δt=t_f≡t\))

Velocity

Your notion of velocity is probably the same as its scientific definition. You know that if you have a large displacement in a small amount of time you have a large velocity, and that velocity has units of distance divided by time, such as miles per hour or kilometers per hour.

Definition: AVERAGE VELOCITY

Average velocity is displacement (change in position) divided by the time of travel,

\[\bar{v}=\frac{Δx}{Δt}=\frac{x_f−x_0}{t_f−t_0}.\]

where \(\bar{v}\) is the average (indicated by the bar over the \(v\)) velocity, \(Δx\) is the change in position (or displacement), and \(x_f\) and \(x_0\) are the final and beginning positions at times \(t_f\) and \(t_0\), respectively. If the starting time \(t_0\) is taken to be zero, then the average velocity is simply

\[\bar{v}=\frac{Δx}{t}.\]

Notice that this definition indicates that velocity is a vector because displacement is a vector. It has both magnitude and direction. The SI unit for velocity is meters per second or m/s, but many other units, such as km/h, mi/h (also written as mph), and cm/s, are in common use. Suppose, for example, an airplane passenger took 5 seconds to move −4 m (the negative sign indicates that displacement is toward the back of the plane). His average velocity would be

\[\bar{v}=\frac{Δx}{t}=\frac{−4\,m}{5\,s}=−0.8 \,m/s.\]

The minus sign indicates the average velocity is also toward the rear of the plane.

The average velocity of an object does not tell us anything about what happens to it between the starting point and ending point, however. For example, we cannot tell from average velocity whether the airplane passenger stops momentarily or backs up before he goes to the back of the plane. To get more details, we must consider smaller segments of the trip over smaller time intervals.

Figure \(\PageIndex{2}\): A more detailed record of an airplane passenger heading toward the back of the plane, showing smaller segments of his trip.

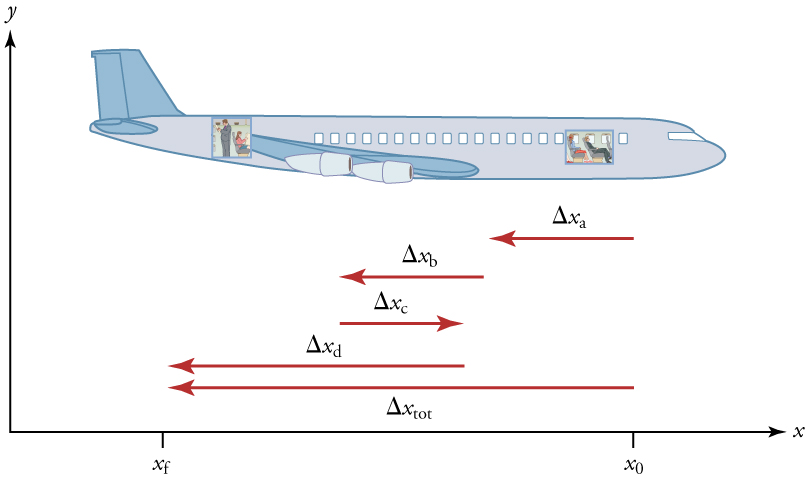
The smaller the time intervals considered in a motion, the more detailed the information. When we carry this process to its logical conclusion, we are left with an infinitesimally small interval. Over such an interval, the average velocity becomes the instantaneous velocity or the velocity at a specific instant. A car’s speedometer, for example, shows the magnitude (but not the direction) of the instantaneous velocity of the car. (Police give tickets based on instantaneous velocity, but when calculating how long it will take to get from one place to another on a road trip, you need to use average velocity.) Instantaneous velocity \(v\) is the average velocity at a specific instant in time (or over an infinitesimally small time interval).

Mathematically, finding instantaneous velocity, \(v\), at a precise instant \(t\) can involve taking a limit, a calculus operation beyond the scope of this text. However, under many circumstances, we can find precise values for instantaneous velocity without calculus.

Speed

In everyday language, most people use the terms “speed” and “velocity” interchangeably. In physics, however, they do not have the same meaning and they are distinct concepts. One major difference is that speed has no direction. Thus speed is a scalar. Just as we need to distinguish between instantaneous velocity and average velocity, we also need to distinguish between instantaneous speed and average speed.

Instantaneous speed is the magnitude of instantaneous velocity. For example, suppose the airplane passenger at one instant had an instantaneous velocity of −3.0 m/s (the minus meaning toward the rear of the plane). At that same time his instantaneous speed was 3.0 m/s. Or suppose that at one time during a shopping trip your instantaneous velocity is 40 km/h due north. Your instantaneous speed at that instant would be 40 km/h—the same magnitude but without a direction. Average speed, however, is very different from average velocity. Average speed is the distance traveled divided by elapsed time.

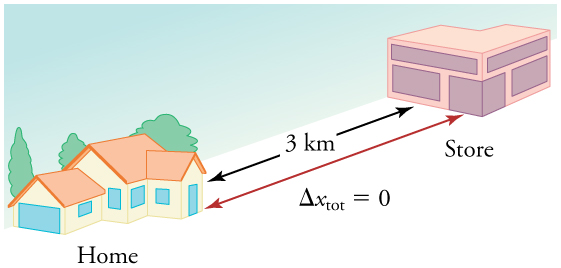
We have noted that distance traveled can be greater than displacement. So average speed can be greater than average velocity, which is displacement divided by time. For example, if you drive to a store and return home in half an hour, and your car’s odometer shows the total distance traveled was 6 km, then your average speed was 12 km/h. Your average velocity, however, was zero, because your displacement for the round trip is zero. (Displacement is change in position and, thus, is zero for a round trip.) Thus average speed is not simply the magnitude of average velocity.

Figure \(\PageIndex{3}\): During a 30-minute round trip to the store, the total distance traveled is 6 km. The average speed is 12 km/h. The displacement for the round trip is zero, since there was no net change in position. Thus the average velocity is zero.

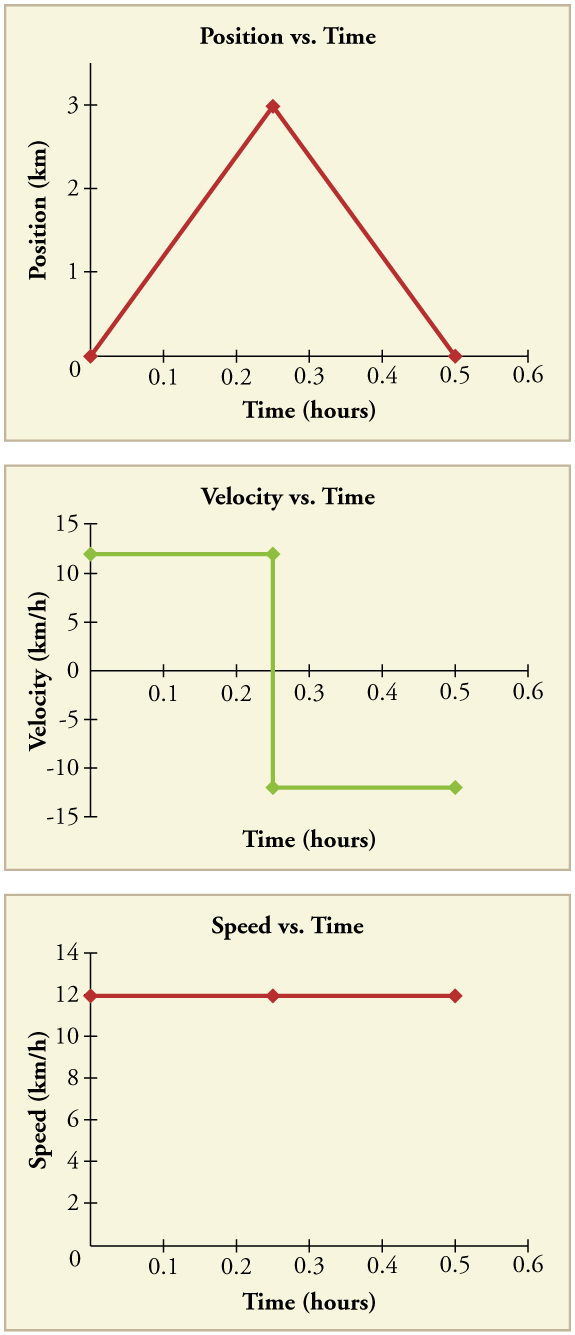
Another way of visualizing the motion of an object is to use a graph. A plot of position or of velocity as a function of time can be very useful. For example, for this trip to the store, the position, velocity, and speed-vs.-time graphs are displayed in Figure \(\PageIndex{4}\). (Note that these graphs depict a very simplified model of the trip. We are assuming that speed is constant during the trip, which is unrealistic given that we’ll probably stop at the store. But for simplicity’s sake, we will model it with no stops or changes in speed. We are also assuming that the route between the store and the house is a perfectly straight line.)

Figure \(\PageIndex{4}\): Position vs. time, velocity vs. time, and speed vs. time on a trip. Note that the velocity for the return trip is negative.

MAKING CONNECTIONS: TAKE-HOME INVESTIGATION - GETTING A SENSE OF SPEED

If you have spent much time driving, you probably have a good sense of speeds between about 10 and 70 miles per hour. But what are these in meters per second? What do we mean when we say that something is moving at 10 m/s? To get a better sense of what these values really mean, do some observations and calculations on your own:

• calculate typical car speeds in meters per second
• estimate jogging and walking speed by timing yourself; convert the measurements into both m/s and mi/h
• determine the speed of an ant, snail, or falling leaf

Exercise \(\PageIndex{1}\)

A commuter train travels from Baltimore to Washington, DC, and back in 1 hour and 45 minutes. The distance between the two stations is approximately 40 miles. What is

1. the average velocity of the train, and
2. the average speed of the train in m/s?

Answer

(a) The average velocity of the train is zero because \(x_f=x_0\); the train ends up at the same place it starts.

(b) The average speed of the train is calculated below. Note that the train travels 40 miles one way and 40 miles back, for a total distance of 80 miles.

\(\frac{distance}{time}=\frac{80 miles}{105 minutes}\)

\(\frac{80 miles}{105 minutes}×\frac{5280 feet}{1 mile}×\frac{1 meter}{3.28 feet}×\frac{1 minute}{60 seconds}=20 m/s\)

Summary

• Time is measured in terms of change, and its SI unit is the second (s). Elapsed time for an event is \[Δt=t_f−t_0 \nonumber,\] where \(t_f\) is the final time and \(t_0\) is the initial time. The initial time is often taken to be zero, as if measured with a stopwatch; the elapsed time is then just \(t\).
• Average velocity \(\bar{v}\) is defined as displacement divided by the travel time. In symbols, average velocity is \[\bar{v}=\frac{Δx}{Δt}=\frac{x_f−x_0}{t_f−t_0} \nonumber.\]
• The SI unit for velocity is m/s.
• Velocity is a vector and thus has a direction.
• Instantaneous velocity \(v\) is the velocity at a specific instant or the average velocity for an infinitesimal interval.
• Instantaneous speed is the magnitude of the instantaneous velocity.
• Instantaneous speed is a scalar quantity, as it has no direction specified.
• Average speed is the total distance traveled divided by the elapsed time. (Average speed is not the magnitude of the average velocity.) Speed is a scalar quantity; it has no direction associated with it.

Glossary

average speed

distance traveled divided by time during which motion occurs

average velocity

displacement divided by time over which displacement occurs

instantaneous velocity

velocity at a specific instant, or the average velocity over an infinitesimal time interval

instantaneous speed

magnitude of the instantaneous velocity

time

change, or the interval over which change occurs

model

simplified description that contains only those elements necessary to describe the physics of a physical situation

elapsed time

the difference between the ending time and beginning time