2.8: Graphical Analysis of One-Dimensional Motion
( \newcommand{\kernel}{\mathrm{null}\,}\)
Learning Objectives
By the end of this section, you will be able to:
- Describe a straight-line graph in terms of its slope and y-intercept.
- Determine average velocity or instantaneous velocity from a graph of position vs. time.
- Determine average or instantaneous acceleration from a graph of velocity vs. time.
- Derive a graph of velocity vs. time from a graph of position vs. time.
- Derive a graph of acceleration vs. time from a graph of velocity vs. time.
A graph, like a picture, is worth a thousand words. Graphs not only contain numerical information; they also reveal relationships between physical quantities. This section uses graphs of displacement, velocity, and acceleration versus time to illustrate one-dimensional kinematics.
Slopes and General Relationships
First note that graphs in this text have perpendicular axes, one horizontal and the other vertical. When two physical quantities are plotted against one another in such a graph, the horizontal axis is usually considered to be an independent variable and the vertical axis a dependent variable. If we call the horizontal axis the x-axis and the vertical axis the y-axis, as in Figure 2.8.1, a straight-line graph has the general form
y=mx+b.
Here m is the slope, defined to be the rise divided by the run of the straight line (Figure 2.8.1). The letter b is used for they-intercept, which is the point at which the line crosses the vertical axis.

Graph of Displacement vs. Time (a = 0, so v is constant)
Time is usually an independent variable that other quantities, such as displacement, depend upon. A graph of displacement versus time would, thus, have on the vertical axis and on the horizontal axis. Figure 2.8.2 is just such a straight-line graph. It shows a graph of displacement versus time for a jet-powered car on a very flat dry lake bed in Nevada.
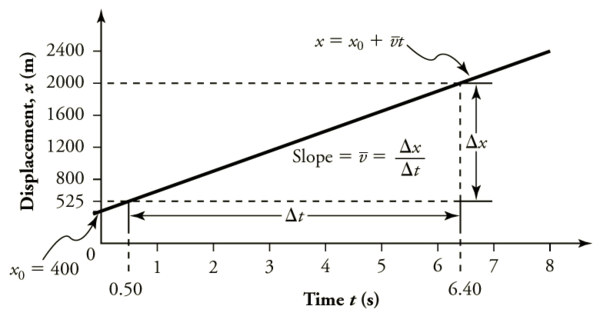
Using the relationship between dependent and independent variables, we see that the slope in the graph above is average velocity ˉv and the intercept is displacement at time zero—that is, x0. Substituting these symbols into y=mx+b gives
x=ˉvt+x0or
x=x0+ˉvt.
Thus a graph of displacement versus time gives a general relationship among displacement, velocity, and time, as well as giving detailed numerical information about a specific situation.
THE SLOPE OF X VS. T
The slope of the graph of displacement x vs. time t is velocity v.
Notice that this equation is the same as that derived algebraically from other motion equations in Motion Equations for Constant Acceleration in One Dimension.
From the figure we can see that the car has a displacement of 25 m at 0.50 s and 2000 m at 6.40 s. Its displacement at other times can be read from the graph; furthermore, information about its velocity and acceleration can also be obtained from the graph.
Example 2.8.1:Determining Average Velocity from a Graph of Displacement versus Time: Jet Car
Find the average velocity of the car whose position is graphed in Figure 2.8.2.
Strategy
The slope of a graph of x vs. t is average velocity, since slope equals rise over run. In this case, rise = change in position and run = change in time, so that
Since the slope is constant here, any two points on the graph can be used to find the slope. (Generally speaking, it is most accurate to use two widely separated points on the straight line. This is because any error in reading data from the graph is proportionally smaller if the interval is larger.)
Solution
- Choose two points on the line. In this case, we choose the points labeled on the graph: (6.4 s, 2000 m) and (0.50 s, 525 m). (Note, however, that you could choose any two points.)
- Substitute the x and t values of the chosen points into the equation. Remember in calculating change (Δ) we always use final value minus initial value. ˉv=ΔxΔt=2000m−525m6.4s−0.50s, yielding v−=250m/s.
Discussion
This is an impressively large land speed (900 km/h, or about 560 mi/h): much greater than the typical highway speed limit of 60 mi/h (27 m/s or 96 km/h), but considerably shy of the record of 343 m/s (1234 km/h or 766 mi/h) set in 1997.
Graphs of Motion when is constant but ≠0
The graphs in Figure 2.8.3 below represent the motion of the jet-powered car as it accelerates toward its top speed, but only during the time when its acceleration is constant. Time starts at zero for this motion (as if measured with a stopwatch), and the displacement and velocity are initially 200 m and 15 m/s, respectively.
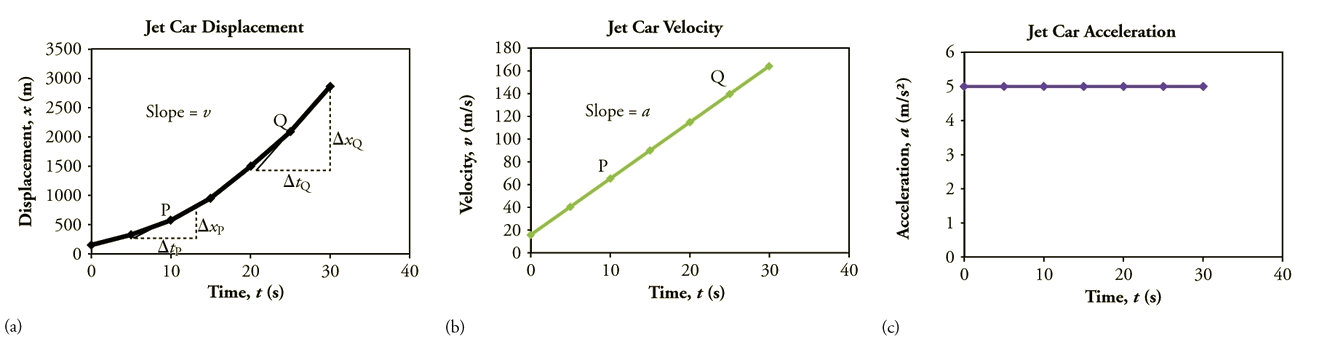
Figure 2.8.3: Graphs of motion of a jet-powered car during the time span when its acceleration is constant. (a) The slope of an x vs. t graph is velocity. This is shown at two points, and the instantaneous velocities obtained are plotted in the next graph. Instantaneous velocity at any point is the slope of the tangent at that point. (b) The slope of the v vs. t graph is constant for this part of the motion, indicating constant acceleration. (c) Acceleration has the constant value of 5.0m/s2 over the time interval plotted.

The graph of displacement versus time in Figure 2.8.3a is a curve rather than a straight line. The slope of the curve becomes steeper as time progresses, showing that the velocity is increasing over time. The slope at any point on a displacement-versus-time graph is the instantaneous velocity at that point. It is found by drawing a straight line tangent to the curve at the point of interest and taking the slope of this straight line. Tangent lines are shown for two points in Figure 2.8.3a. If this is done at every point on the curve and the values are plotted against time, then the graph of velocity versus time shown in Figure 2.8.3b is obtained. Furthermore, the slope of the graph of velocity versus time is acceleration, which is shown in Figure 2.8.3c.
Example 2.8.2:
Calculate the velocity of the jet car at a time of 25 s by finding the slope of the \(\displaystyle vs. \(\displaystyle graph in the graph below
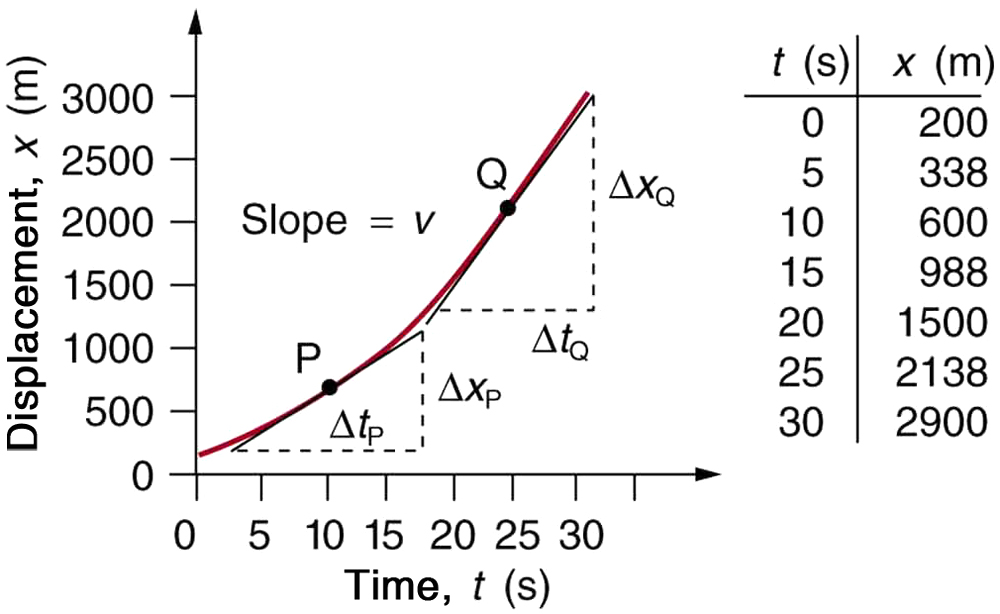
Strategy
The slope of a curve at a point is equal to the slope of a straight line tangent to the curve at that point. This principle is illustrated in Figure, where Q is the point at t=25s.
Solution
- Find the tangent line to the curve at t=25s.
- Determine the endpoints of the tangent. These correspond to a position of 1300 m at time 19 s and a position of 3120 m at time 32 s.
- Plug these endpoints into the equation to solve for the slope, .
slope=vQ=ΔxQΔtQ=(3120m−1300m)(32s−19s)
Thus,
Discussion
This is the value given in this figure’s table for v at t=25s. The value of 140 m/s for vQ is plotted in Figure. The entire graph of v vs. t can be obtained in this fashion.
Carrying this one step further, we note that the slope of a velocity versus time graph is acceleration. Slope is rise divided by run; on a v vs. t graph, rise = change in velocity Δv and run = change in time Δt.
THE SLOPE OF V VS. T
The slope of a graph of velocity v vs. time t is acceleration a.
slope=ΔvΔt=a
Since the velocity versus time graph in Figure 2.8.3b is a straight line, its slope is the same everywhere, implying that acceleration is constant. Acceleration versus time is graphed in Figure(c).
Additional general information can be obtained from Figure and the expression for a straight line, y=mx+b.
In this case, the vertical axis y is V, the intercept b is v0, the slope m is a, and the horizontal axis x is t. Substituting these symbols yields
v=v0+at.
A general relationship for velocity, acceleration, and time has again been obtained from a graph. Notice that this equation was also derived algebraically from other motion equations in Motion Equations for Constant Acceleration in One Dimension.
It is not accidental that the same equations are obtained by graphical analysis as by algebraic techniques. In fact, an important way to discover physical relationships is to measure various physical quantities and then make graphs of one quantity against another to see if they are correlated in any way. Correlations imply physical relationships and might be shown by smooth graphs such as those above. From such graphs, mathematical relationships can sometimes be postulated. Further experiments are then performed to determine the validity of the hypothesized relationships.
Graphs of Motion Where Acceleration is Not Constant
Now consider the motion of the jet car as it goes from 165 m/s to its top velocity of 250 m/s, graphed in Figure 2.8.6. Time again starts at zero, and the initial position and velocity are 2900 m and 165 m/s, respectively. (These were the final position and velocity of the car in the motion graphed in Figure 2.8.4) Acceleration gradually decreases from 5.0m/s2 to zero when the car hits 250 m/s. The slope of the x vs. t graph increases until t=55s, after which time the slope is constant. Similarly, velocity increases until 55 s and then becomes constant, since acceleration decreases to zero at 55 s and remains zero afterward.
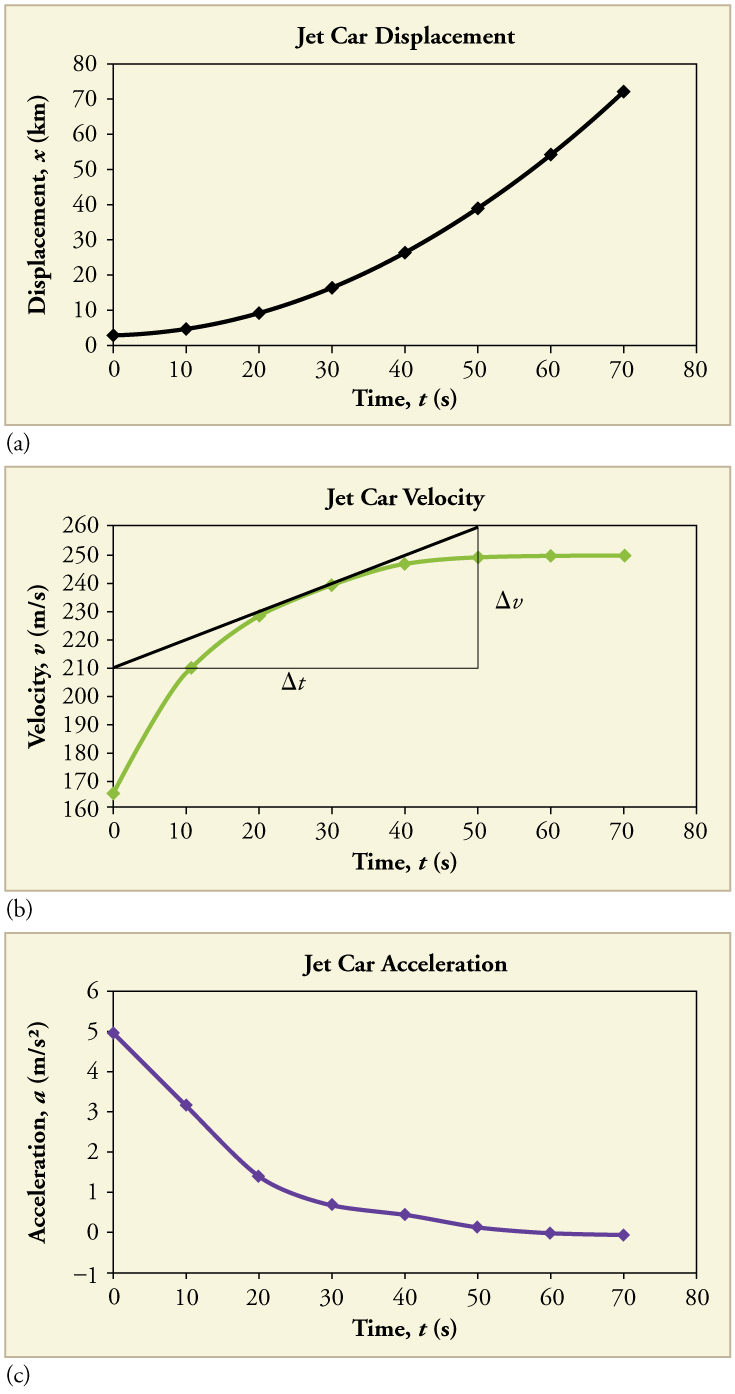
Example 2.8.3:Calculating Acceleration from a Graph of Velocity versus Time
Calculate the acceleration of the jet car at a time of 25 s by finding the slope of the v vs. t graph in Figure 2.8.6b.
Strategy
The slope of the curve at t=25s is equal to the slope of the line tangent at that point, as illustrated in Figure 2.8.6b.
Solution
Determine endpoints of the tangent line from the figure, and then plug them into the equation to solve for slope, .
Discussion
Note that this value for a is consistent with the value plotted in Figure(c) at t=25s.
A graph of displacement versus time can be used to generate a graph of velocity versus time, and a graph of velocity versus time can be used to generate a graph of acceleration versus time. We do this by finding the slope of the graphs at every point. If the graph is linear (i.e., a line with a constant slope), it is easy to find the slope at any point and you have the slope for every point. Graphical analysis of motion can be used to describe both specific and general characteristics of kinematics. Graphs can also be used for other topics in physics. An important aspect of exploring physical relationships is to graph them and look for underlying relationships.
Exercise 2.8.1:Check Your Understanding
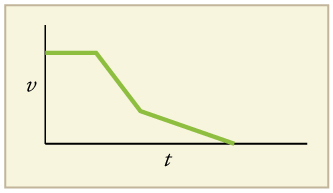
A graph of velocity vs. time of a ship coming into a harbor is shown below.
- Describe the motion of the ship based on the graph.
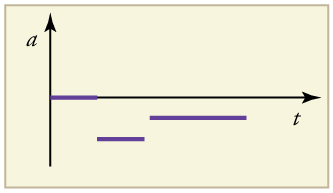
- What would a graph of the ship’s acceleration look like?
- Answer a
-
(a) The ship moves at constant velocity and then begins to decelerate at a constant rate. At some point, its deceleration rate decreases. It maintains this lower deceleration rate until it stops moving.
Solution b
A graph of acceleration vs. time would show zero acceleration in the first leg, large and constant negative acceleration in the second leg, and constant negative acceleration.
Summary
- Graphs of motion can be used to analyze motion.
- Graphical solutions yield identical solutions to mathematical methods for deriving motion equations.
- The slope of a graph of displacement x vs. time t is velocity v.
- The slope of a graph of velocity v vs. time t graph is acceleration a.
- Average velocity, instantaneous velocity, and acceleration can all be obtained by analyzing graphs.
Glossary
- independent variable
- the variable that the dependent variable is measured with respect to; usually plotted along the x-axis
- dependent variable
- the variable that is being measured; usually plotted along the y-axis
- slope
- the difference in y-value (the rise) divided by the difference in x-value (the run) of two points on a straight line
- y-intercept
- the y-value when x=0, or when the graph crosses the y-axis


