15.E: Heat and Heat Transfer Methods (Exercise)
- Last updated
- Save as PDF
- Page ID
- 15418
Conceptual Questions
15.1: The First Law of Thermodynamics
1. Describe the photo of the tea kettle at the beginning of this section in terms of heat transfer, work done, and internal energy. How is heat being transferred? What is the work done and what is doing it? How does the kettle maintain its internal energy?
2. The first law of thermodynamics and the conservation of energy, as discussed in Conservation of Energy, are clearly related. How do they differ in the types of energy considered?
3. Heat transfer \(\displaystyle Q\) and work done \(\displaystyle W\) are always energy in transit, whereas internal energy \(\displaystyle U\) is energy stored in a system. Give an example of each type of energy, and state specifically how it is either in transit or resides in a system.
4. How do heat transfer and internal energy differ? In particular, which can be stored as such in a system and which cannot?
5. If you run down some stairs and stop, what happens to your kinetic energy and your initial gravitational potential energy?
6. Give an explanation of how food energy (calories) can be viewed as molecular potential energy (consistent with the atomic and molecular definition of internal energy).
7. Identify the type of energy transferred to your body in each of the following as either internal energy, heat transfer, or doing work:
(a) basking in sunlight;
(b) eating food;
(c) riding an elevator to a higher floor.
15.2: The First Law of Thermodynamics and Some Simple Processes
8. A great deal of effort, time, and money has been spent in the quest for the so-called perpetual-motion machine, which is defined as a hypothetical machine that operates or produces useful work indefinitely and/or a hypothetical machine that produces more work or energy than it consumes. Explain, in terms of heat engines and the first law of thermodynamics, why or why not such a machine is likely to be constructed.
9. One method of converting heat transfer into doing work is for heat transfer into a gas to take place, which expands, doing work on a piston, as shown in the figure below.
(a) Is the heat transfer converted directly to work in an isobaric process, or does it go through another form first? Explain your answer.
(b) What about in an isothermal process?
(c) What about in an adiabatic process (where heat transfer occurred prior to the adiabatic process)?
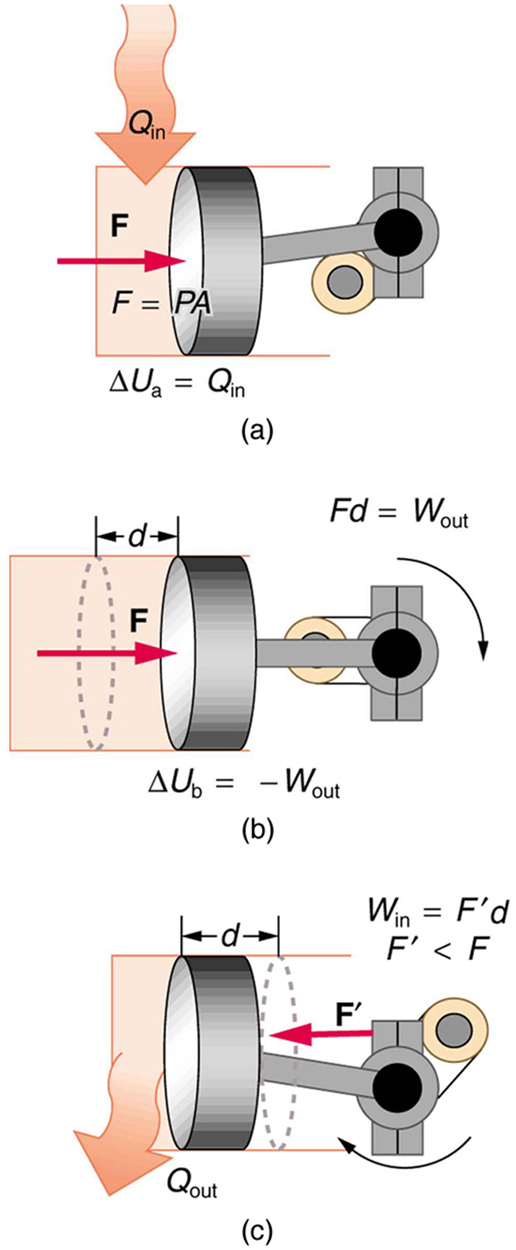
10. Would the previous question make any sense for an isochoric process? Explain your answer.
11. We ordinarily say that \(\displaystyle ΔU=0\) for an isothermal process. Does this assume no phase change takes place? Explain your answer.
12. The temperature of a rapidly expanding gas decreases. Explain why in terms of the first law of thermodynamics. (Hint: Consider whether the gas does work and whether heat transfer occurs rapidly into the gas through conduction.)
13. Which cyclical process represented by the two closed loops, ABCFA and ABDEA, on the \(\displaystyle PV\) diagram in the figure below produces the greatest net work? Is that process also the one with the smallest work input required to return it to point A? Explain your responses.
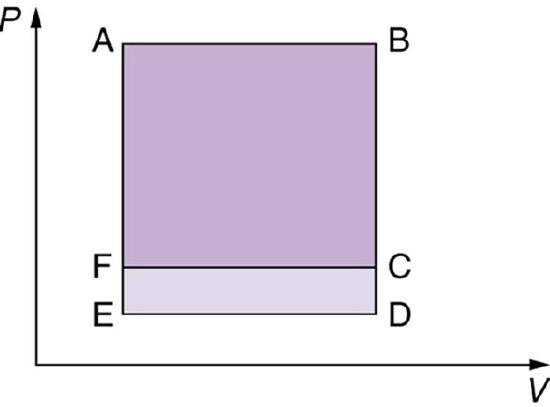
The two cyclical processes shown on this \(\displaystyle PV\) diagram start with and return the system to the conditions at point A, but they follow different paths and produce different amounts of work.
14. A real process may be nearly adiabatic if it occurs over a very short time. How does the short time span help the process to be adiabatic?
15. It is unlikely that a process can be isothermal unless it is a very slow process. Explain why. Is the same true for isobaric and isochoric processes? Explain your answer.
15.3 Introduction to the Second Law of Thermodynamics: Heat Engines and Their Efficiency
16. Imagine you are driving a car up Pike’s Peak in Colorado. To raise a car weighing 1000 kilograms a distance of 100 meters would require about a million joules. You could raise a car 12.5 kilometers with the energy in a gallon of gas. Driving up Pike's Peak (a mere 3000-meter climb) should consume a little less than a quart of gas. But other considerations have to be taken into account. Explain, in terms of efficiency, what factors may keep you from realizing your ideal energy use on this trip.
17. Is a temperature difference necessary to operate a heat engine? State why or why not.
18. Definitions of efficiency vary depending on how energy is being converted. Compare the definitions of efficiency for the human body and heat engines. How does the definition of efficiency in each relate to the type of energy being converted into doing work?
19. Why—other than the fact that the second law of thermodynamics says reversible engines are the most efficient—should heat engines employing reversible processes be more efficient than those employing irreversible processes? Consider that dissipative mechanisms are one cause of irreversibility.
15.4 Carnot’s Perfect Heat Engine: The Second Law of Thermodynamics Restated
20. Think about the drinking bird at the beginning of this section (Figure). Although the bird enjoys the theoretical maximum efficiency possible, if left to its own devices over time, the bird will cease “drinking.” What are some of the dissipative processes that might cause the bird’s motion to cease?
21. Can improved engineering and materials be employed in heat engines to reduce heat transfer into the environment? Can they eliminate heat transfer into the environment entirely?
22. Does the second law of thermodynamics alter the conservation of energy principle?
15.5: Applications of Thermodynamics: Heat Pumps and Refrigerators
23. Explain why heat pumps do not work as well in very cold climates as they do in milder ones. Is the same true of refrigerators?
24. In some Northern European nations, homes are being built without heating systems of any type. They are very well insulated and are kept warm by the body heat of the residents. However, when the residents are not at home, it is still warm in these houses. What is a possible explanation?
25. Why do refrigerators, air conditioners, and heat pumps operate most cost-effectively for cycles with a small difference between \(\displaystyle T_h\) and \(\displaystyle T_c\)? (Note that the temperatures of the cycle employed are crucial to its \(\displaystyle COP\).)
26. Grocery store managers contend that there is less total energy consumption in the summer if the store is kept at a low temperature. Make arguments to support or refute this claim, taking into account that there are numerous refrigerators and freezers in the store.
27. Can you cool a kitchen by leaving the refrigerator door open?
15.6: Entropy and the Second Law of Thermodynamics: Disorder and the Unavailability of Energy
28. A woman shuts her summer cottage up in September and returns in June. No one has entered the cottage in the meantime. Explain what she is likely to find, in terms of the second law of thermodynamics.
29. Consider a system with a certain energy content, from which we wish to extract as much work as possible. Should the system’s entropy be high or low? Is this orderly or disorderly? Structured or uniform? Explain briefly.
30. Does a gas become more orderly when it liquefies? Does its entropy change? If so, does the entropy increase or decrease? Explain your answer.
31. Explain how water’s entropy can decrease when it freezes without violating the second law of thermodynamics. Specifically, explain what happens to the entropy of its surroundings.
32. Is a uniform-temperature gas more or less orderly than one with several different temperatures? Which is more structured? In which can heat transfer result in work done without heat transfer from another system?
33. Give an example of a spontaneous process in which a system becomes less ordered and energy becomes less available to do work. What happens to the system’s entropy in this process?
34. What is the change in entropy in an adiabatic process? Does this imply that adiabatic processes are reversible? Can a process be precisely adiabatic for a macroscopic system?
35. Does the entropy of a star increase or decrease as it radiates? Does the entropy of the space into which it radiates (which has a temperature of about 3 K) increase or decrease? What does this do to the entropy of the universe?
36. Explain why a building made of bricks has smaller entropy than the same bricks in a disorganized pile. Do this by considering the number of ways that each could be formed (the number of microstates in each macrostate).
15.7: Statistical Interpretation of Entropy and the Second Law of Thermodynamics: The Underlying Explanation
37. Explain why a building made of bricks has smaller entropy than the same bricks in a disorganized pile. Do this by considering the number of ways that each could be formed (the number of microstates in each macrostate).
Problems & Exercises
15.1: The First Law of Thermodynamics
38. What is the change in internal energy of a car if you put 12.0 gal of gasoline into its tank? The energy content of gasoline is \(\displaystyle 1.3×10^8J/gal\). All other factors, such as the car’s temperature, are constant.
Solution
\(\displaystyle 1.6×10^9J\)
39. How much heat transfer occurs from a system, if its internal energy decreased by 150 J while it was doing 30.0 J of work?
40. A system does \(\displaystyle 1.80×10^8J\) of work while \(\displaystyle 7.50×10^8J\) of heat transfer occurs to the environment. What is the change in internal energy of the system assuming no other changes (such as in temperature or by the addition of fuel)?
Solution
\(\displaystyle −9.30×10^8J\)
41. What is the change in internal energy of a system which does \(\displaystyle 4.50×10^5J\) of work while \(\displaystyle 3.00×10^6J\) of heat transfer occurs into the system, and \(\displaystyle 8.00×10^6J\) of heat transfer occurs to the environment?
42. Suppose a woman does 500 J of work and 9500 J of heat transfer occurs into the environment in the process.
(a) What is the decrease in her internal energy, assuming no change in temperature or consumption of food? (That is, there is no other energy transfer.)
(b) What is her efficiency?
Solution
(a) \(\displaystyle −1.0×10^4J\), or \(\displaystyle −2.39 kcal\)
(b) 5.00%
43. (a) How much food energy will a man metabolize in the process of doing 35.0 kJ of work with an efficiency of 5.00%?
(b) How much heat transfer occurs to the environment to keep his temperature constant? Explicitly show how you follow the steps in the Problem-Solving Strategy for thermodynamics found in Problem-Solving Strategies for Thermodynamics.
44. (a) What is the average metabolic rate in watts of a man who metabolizes 10,500 kJ of food energy in one day?
(b) What is the maximum amount of work in joules he can do without breaking down fat, assuming a maximum efficiency of 20.0%?
(c) Compare his work output with the daily output of a 187-W (0.250-horsepower) motor.
Solution
(a) 122 W
(b) \(\displaystyle 2.10×10^6J\)
(c) Work done by the motor is \(\displaystyle 1.61×10^7\); thus the motor produces 7.67 times the work done by the man
45. (a) How long will the energy in a 1470-kJ (350-kcal) cup of yogurt last in a woman doing work at the rate of 150 W with an efficiency of 20.0% (such as in leisurely climbing stairs)?
(b) Does the time found in part (a) imply that it is easy to consume more food energy than you can reasonably expect to work off with exercise?
46. (a) A woman climbing the Washington Monument metabolizes \(\displaystyle 6.00×10^2kJ\) of food energy. If her efficiency is 18.0%, how much heat transfer occurs to the environment to keep her temperature constant?
(b) Discuss the amount of heat transfer found in (a). Is it consistent with the fact that you quickly warm up when exercising?
Solution
(a) 492 kJ
(b) This amount of heat is consistent with the fact that you warm quickly when exercising. Since the body is inefficient, the excess heat produced must be dissipated through sweating, breathing, etc.
15.2: The First Law of Thermodynamics and Some Simple Processes
47. A car tire contains \(\displaystyle 0.0380m^3\) of air at a pressure of \(\displaystyle 2.20×10^5N/m^2\) (about 32 psi). How much more internal energy does this gas have than the same volume has at zero gauge pressure (which is equivalent to normal atmospheric pressure)?
Solution
\(\displaystyle 6.77×10^3J\)
48. A helium-filled toy balloon has a gauge pressure of 0.200 atm and a volume of 10.0 L. How much greater is the internal energy of the helium in the balloon than it would be at zero gauge pressure?
49. Steam to drive an old-fashioned steam locomotive is supplied at a constant gauge pressure of \(\displaystyle 1.75×10^6N/m^2\) (about 250 psi) to a piston with a 0.200-m radius.
(a) By calculating \(\displaystyle PΔV\), find the work done by the steam when the piston moves 0.800 m. Note that this is the net work output, since gauge pressure is used.
(b) Now find the amount of work by calculating the force exerted times the distance traveled. Is the answer the same as in part (a)?
Solution
(a) \(\displaystyle W=PΔV=1.76×10^5J\)
(b) \(\displaystyle W=Fd=1.76×10^5J\). Yes, the answer is the same.
50. A hand-driven tire pump has a piston with a 2.50-cm diameter and a maximum stroke of 30.0 cm. (a) How much work do you do in one stroke if the average gauge pressure is \(\displaystyle 2.40×10^5N/m^2\) (about 35 psi)?
(b) What average force do you exert on the piston, neglecting friction and gravitational force?
51. Calculate the net work output of a heat engine following path ABCDA in the figure below.
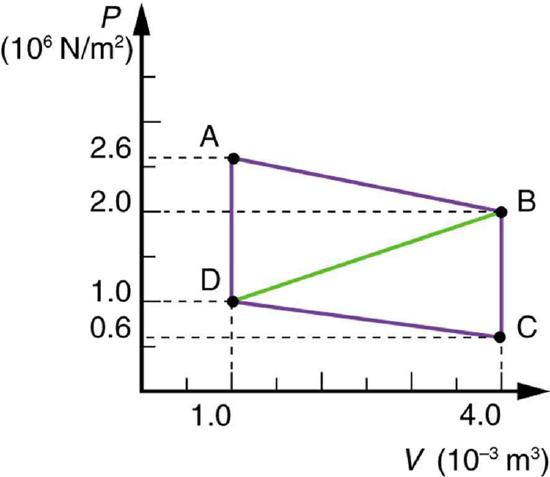
Solution
\(\displaystyle W=4.5×10^3J\)
52. What is the net work output of a heat engine that follows path ABDA in the figure above, with a straight line from B to D? Why is the work output less than for path ABCDA? Explicitly show how you follow the steps in the Problem-Solving Strategies for Thermodynamics.
53. Unreasonable Results
What is wrong with the claim that a cyclical heat engine does 4.00 kJ of work on an input of 24.0 kJ of heat transfer while 16.0 kJ of heat transfers to the environment?
Solution
\(\displaystyle W\) is not equal to the difference between the heat input and the heat output.
54. (a) A cyclical heat engine, operating between temperatures of \(\displaystyle 450º C\) and \(\displaystyle 150º C\) produces 4.00 MJ of work on a heat transfer of 5.00 MJ into the engine. How much heat transfer occurs to the environment?
(b) What is unreasonable about the engine?
(c) Which premise is unreasonable?
55. Construct Your Own Problem
Consider a car’s gasoline engine. Construct a problem in which you calculate the maximum efficiency this engine can have. Among the things to consider are the effective hot and cold reservoir temperatures. Compare your calculated efficiency with the actual efficiency of car engines.
56. Construct Your Own Problem
Consider a car trip into the mountains. Construct a problem in which you calculate the overall efficiency of the car for the trip as a ratio of kinetic and potential energy gained to fuel consumed. Compare this efficiency to the thermodynamic efficiency quoted for gasoline engines and discuss why the thermodynamic efficiency is so much greater. Among the factors to be considered are the gain in altitude and speed, the mass of the car, the distance traveled, and typical fuel economy.
15.3 Introduction to the Second Law of Thermodynamics: Heat Engines and Their Efficiency
57. A certain heat engine does 10.0 kJ of work and 8.50 kJ of heat transfer occurs to the environment in a cyclical process.
(a) What was the heat transfer into this engine?
(b) What was the engine’s efficiency?
Solution
(a) \(\displaystyle 18.5kJ\)
(b) \(\displaystyle 54.1%\)
58. With \(\displaystyle 2.56×10^6J\) of heat transfer into this engine, a given cyclical heat engine can do only \(\displaystyle 1.50×10^5J\) of work.
(a) What is the engine’s efficiency?
(b) How much heat transfer to the environment takes place?
59. (a) What is the work output of a cyclical heat engine having a 22.0% efficiency and \(\displaystyle 6.00×10^9J\) of heat transfer into the engine?
(b) How much heat transfer occurs to the environment?
Solution
(a) \(\displaystyle 1.32 × 10^9J\)
(b) \(\displaystyle 4.68 × 10^9J\)
60. (a) What is the efficiency of a cyclical heat engine in which 75.0 kJ of heat transfer occurs to the environment for every 95.0 kJ of heat transfer into the engine?
(b) How much work does it produce for 100 kJ of heat transfer into the engine?
61. The engine of a large ship does \(\displaystyle 2.00×10^8J\) of work with an efficiency of 5.00%.
(a) How much heat transfer occurs to the environment?
(b) How many barrels of fuel are consumed, if each barrel produces \(\displaystyle 6.00×10^9J\) of heat transfer when burned?
Solution
(a) \(\displaystyle 3.80 × 10^9J\)
(b) 0.667 barrels
62. (a) How much heat transfer occurs to the environment by an electrical power station that uses \(\displaystyle 1.25×10^{14}J\) of heat transfer into the engine with an efficiency of 42.0%?
(b) What is the ratio of heat transfer to the environment to work output?
(c) How much work is done?
63. Assume that the turbines at a coal-powered power plant were upgraded, resulting in an improvement in efficiency of 3.32%. Assume that prior to the upgrade the power station had an efficiency of 36% and that the heat transfer into the engine in one day is still the same at \(\displaystyle 2.50×10^{14}J\).
(a) How much more electrical energy is produced due to the upgrade?
(b) How much less heat transfer occurs to the environment due to the upgrade?
Solution
(a) \(\displaystyle 8.30 × 10^{12}J\), which is 3.32% of \(\displaystyle 2.50 × 10^{14}J\).
(b) \(\displaystyle –8.30 × 10^{12}J\), where the negative sign indicates a reduction in heat transfer to the environment.
64. This problem compares the energy output and heat transfer to the environment by two different types of nuclear power stations—one with the normal efficiency of 34.0%, and another with an improved efficiency of 40.0%. Suppose both have the same heat transfer into the engine in one day, \(\displaystyle 2.50×10^{14}J\).
(a) How much more electrical energy is produced by the more efficient power station?
(b) How much less heat transfer occurs to the environment by the more efficient power station? (One type of more efficient nuclear power station, the gas-cooled reactor, has not been reliable enough to be economically feasible in spite of its greater efficiency.)
15.4 Carnot’s Perfect Heat Engine: The Second Law of Thermodynamics Restated
65. A certain gasoline engine has an efficiency of 30.0%. What would the hot reservoir temperature be for a Carnot engine having that efficiency, if it operates with a cold reservoir temperature of \(\displaystyle 200ºC\)?
Solution
\(\displaystyle 403ºC\)
66. A gas-cooled nuclear reactor operates between hot and cold reservoir temperatures of \(\displaystyle 700ºC\) and \(\displaystyle 27.0ºC\).
(a) What is the maximum efficiency of a heat engine operating between these temperatures?
(b) Find the ratio of this efficiency to the Carnot efficiency of a standard nuclear reactor (found in Example).
67. (a) What is the hot reservoir temperature of a Carnot engine that has an efficiency of 42.0% and a cold reservoir temperature of \(\displaystyle 27.0ºC\)?
(b) What must the hot reservoir temperature be for a real heat engine that achieves 0.700 of the maximum efficiency, but still has an efficiency of 42.0% (and a cold reservoir at \(\displaystyle 27.0ºC\)?
(c) Does your answer imply practical limits to the efficiency of car gasoline engines?
Solution
(a) \(\displaystyle 244ºC\)
(b) \(\displaystyle 477ºC\)
(c) Yes, since automobiles engines cannot get too hot without overheating, their efficiency is limited.
68. Steam locomotives have an efficiency of 17.0% and operate with a hot steam temperature of \(\displaystyle 425ºC\).
(a) What would the cold reservoir temperature be if this were a Carnot engine?
(b) What would the maximum efficiency of this steam engine be if its cold reservoir temperature were \(\displaystyle 150ºC\)?
69. Practical steam engines utilize \(\displaystyle 450ºC\) steam, which is later exhausted at \(\displaystyle 270ºC\).
(a) What is the maximum efficiency that such a heat engine can have?
(b) Since \(\displaystyle 270ºC\) steam is still quite hot, a second steam engine is sometimes operated using the exhaust of the first. What is the maximum efficiency of the second engine if its exhaust has a temperature of \(\displaystyle 150ºC\)?
(c) What is the overall efficiency of the two engines?
(d) Show that this is the same efficiency as a single Carnot engine operating between \(\displaystyle 450ºC\) and \(\displaystyle 150ºC\). Explicitly show how you follow the steps in the Problem-Solving Strategies for Thermodynamics.
Solution
(a) \(\displaystyle Eff_1=1−\frac{T_{c,1}}{T_{h,1}}=1−\frac{543K}{723K}=0.249\) or \(\displaystyle 24.9%\)
(b) \(\displaystyle Eff_2=1−\frac{423K}{543K}=0.221\) or \(\displaystyle 22.1%\)
(c) \(\displaystyle Eff_1=1−\frac{T_{c,1}}{T_{h,1}}⇒T_{c,1}=T_{h,1}(1,−,eff_1)\) similarly, \(\displaystyle T_{c,2}=T_{h,2}(1−Eff_2)\)
using \(\displaystyle T_{h,2}=T_{c,1} \text{in above equation gives} T_{c,2}=T_{h,1}(1−Eff_1)(1−Eff_2)≡T_{h,1}(1−Eff_{overall})\)
\(\displaystyle ∴(1−Eff_{overall})=(1−Eff_1)(1−Eff_2)\)
\(\displaystyle Eff_{overall}=1−(1−0.249)(1−0.221)=41.5%\)
(d) \(\displaystyle Eff_{overall}=1−\frac{423K}{723K}=0.415\) or \(\displaystyle 41.5%\)
70. A coal-fired electrical power station has an efficiency of 38%. The temperature of the steam leaving the boiler is \(\displaystyle 550ºC \). What percentage of the maximum efficiency does this station obtain? (Assume the temperature of the environment is \(\displaystyle 20ºC\).)
71. Would you be willing to financially back an inventor who is marketing a device that she claims has 25 kJ of heat transfer at 600 K, has heat transfer to the environment at 300 K, and does 12 kJ of work? Explain your answer.
Solution
The heat transfer to the cold reservoir is \(\displaystyle Q_c=Q_h−W=25kJ−12kJ=13kJ\), so the efficiency is \(\displaystyle Eff=1−\frac{Q_c}{Q_h}=1−\frac{13kJ}{25kJ}=0.48\). The Carnot efficiency is \(\displaystyle Eff_C=1−\frac{T_c}{T_h}=1−\frac{300K}{600K}=0.50\). The actual efficiency is 96% of the Carnot efficiency, which is much higher than the best-ever achieved of about 70%, so her scheme is likely to be fraudulent.
72. Unreasonable Results
(a) Suppose you want to design a steam engine that has heat transfer to the environment at 270ºC and has a Carnot efficiency of 0.800. What temperature of hot steam must you use?
(b) What is unreasonable about the temperature?
(c) Which premise is unreasonable?
73. Unreasonable Results
(a) Calculate the cold reservoir temperature of a steam engine that uses hot steam at \(\displaystyle 450ºC\) and has a Carnot efficiency of 0.700.
(b) What is unreasonable about the temperature?
(c) Which premise is unreasonable?
Solution
(a) –56.3ºC
(b) The temperature is too cold for the output of a steam engine (the local environment). It is below the freezing point of water.
(c) The assumed efficiency is too high.
15.5: Applications of Thermodynamics: Heat Pumps and Refrigerators
74. What is the coefficient of performance of an ideal heat pump that has heat transfer from a cold temperature of \(\displaystyle −25.0ºC\) to a hot temperature of \(\displaystyle 40.0ºC\)?
Solution
4.82
75. Suppose you have an ideal refrigerator that cools an environment at \(\displaystyle −20.0ºC\) and has heat transfer to another environment at \(\displaystyle 50.0ºC\). What is its coefficient of performance?
76. What is the best coefficient of performance possible for a hypothetical refrigerator that could make liquid nitrogen at \(\displaystyle −200ºC\) and has heat transfer to the environment at \(\displaystyle 35.0ºC\)?
Solution
0.311
77. In a very mild winter climate, a heat pump has heat transfer from an environment at \(\displaystyle 5.00ºC\) to one at \(\displaystyle 35.0ºC\). What is the best possible coefficient of performance for these temperatures? Explicitly show how you follow the steps in the Problem-Solving Strategies for Thermodynamics.
78. (a) What is the best coefficient of performance for a heat pump that has a hot reservoir temperature of \(\displaystyle 50.0ºC\) and a cold reservoir temperature of \(\displaystyle −20.0ºC\)?
(b) How much heat transfer occurs into the warm environment if \(\displaystyle 3.60×10^7J\) of work (10.0kW⋅h) is put into it?
(c) If the cost of this work input is \(\displaystyle 10.0 cents/kW⋅h\), how does its cost compare with the direct heat transfer achieved by burning natural gas at a cost of 85.0 cents per therm. (A therm is a common unit of energy for natural gas and equals \(\displaystyle 1.055×10^8J\).)
Solution
(a) 4.61
(b) \(\displaystyle 1.66×10^8J\) or \(\displaystyle 3.97×10^4kcal\)
(c) To transfer \(\displaystyle 1.66×10^8J\), heat pump costs $1.00, natural gas costs $1.34.
79. (a) What is the best coefficient of performance for a refrigerator that cools an environment at \(\displaystyle −30.0ºC\) and has heat transfer to another environment at \(\displaystyle 45.0ºC\)?
(b) How much work in joules must be done for a heat transfer of 4186 kJ from the cold environment?
(c) What is the cost of doing this if the work costs 10.0 cents per \(\displaystyle 3.60×10^6J\)?
(d) How many kJ of heat transfer occurs into the warm environment?
(e) Discuss what type of refrigerator might operate between these temperatures.
80. Suppose you want to operate an ideal refrigerator with a cold temperature of \(\displaystyle −10.0ºC\), and you would like it to have a coefficient of performance of 7.00. What is the hot reservoir temperature for such a refrigerator?
Solution
27.6ºC
81. An ideal heat pump is being considered for use in heating an environment with a temperature of \(\displaystyle 22.0ºC\). What is the cold reservoir temperature if the pump is to have a coefficient of performance of 12.0?
82. A 4-ton air conditioner removes \(\displaystyle 5.06×10^7J\) (48,000 British thermal units) from a cold environment in 1.00 h.
(a) What energy input in joules is necessary to do this if the air conditioner has an energy efficiency rating (\(\displaystyle EER\)) of 12.0?
(b) What is the cost of doing this if the work costs 10.0 cents per \(\displaystyle 3.60×10^6J \) (one kilowatt-hour)?
(c) Discuss whether this cost seems realistic. Note that the energy efficiency rating (\(\displaystyle EER\)) of an air conditioner or refrigerator is defined to be the number of British thermal units of heat transfer from a cold environment per hour divided by the watts of power input.
Solution
(a) \(\displaystyle 1.44×10^7J\)
(b) 40 cents
(c) This cost seems quite realistic; it says that running an air conditioner all day would cost $9.59 (if it ran continuously).
83. Show that the coefficients of performance of refrigerators and heat pumps are related by \(\displaystyle COP_{ref}=COP_{hp}−1\).
Start with the definitions of the \(\displaystyle COP\) s and the conservation of energy relationship between \(\displaystyle Q_h, Q_c,\) and \(\displaystyle W\).
15.6: Entropy and the Second Law of Thermodynamics: Disorder and the Unavailability of Energy
84. (a) On a winter day, a certain house loses \(\displaystyle 5.00×10^8J\) of heat to the outside (about 500,000 Btu). What is the total change in entropy due to this heat transfer alone, assuming an average indoor temperature of \(\displaystyle 21.0º C\) and an average outdoor temperature of \(\displaystyle 5.00º C\)?
(b) This large change in entropy implies a large amount of energy has become unavailable to do work. Where do we find more energy when such energy is lost to us?
Solution
(a) \(\displaystyle 9.78×10^4J/K\)
(b) In order to gain more energy, we must generate it from things within the house, like a heat pump, human bodies, and other appliances. As you know, we use a lot of energy to keep our houses warm in the winter because of the loss of heat to the outside.
85. On a hot summer day, \(\displaystyle 4.00×10^6J\) of heat transfer into a parked car takes place, increasing its temperature from \(\displaystyle 35.0º C\) to \(\displaystyle 45.0º C\). What is the increase in entropy of the car due to this heat transfer alone?
86. A hot rock ejected from a volcano’s lava fountain cools from \(\displaystyle 1100º C\) to \(\displaystyle 40.0º C\), and its entropy decreases by 950 J/K. How much heat transfer occurs from the rock?
Solution
\(\displaystyle 8.01×10^5J\)
87. When \(\displaystyle 1.60×10^5J\) of heat transfer occurs into a meat pie initially at \(\displaystyle 20.0º C\), its entropy increases by 480 J/K. What is its final temperature?
88. The Sun radiates energy at the rate of \(\displaystyle 3.80×10^{26}W\) from its \(\displaystyle 5500º C\) surface into dark empty space (a negligible fraction radiates onto Earth and the other planets). The effective temperature of deep space is \(\displaystyle −270º C\).
(a) What is the increase in entropy in one day due to this heat transfer?
(b) How much work is made unavailable?
Solution
(a) \(\displaystyle 1.04×10^{31}J/K\)
(b) \(\displaystyle 3.28×10^{31}J\)
89. (a) In reaching equilibrium, how much heat transfer occurs from 1.00 kg of water at \(\displaystyle 40.0º C\) when it is placed in contact with 1.00 kg of \(\displaystyle 20.0º C\) water in reaching equilibrium?
(b) What is the change in entropy due to this heat transfer?
(c) How much work is made unavailable, taking the lowest temperature to be \(\displaystyle 20.0º C\)? Explicitly show how you follow the steps in the Problem-Solving Strategies for Entropy.
90. What is the decrease in entropy of 25.0 g of water that condenses on a bathroom mirror at a temperature of \(\displaystyle 35.0º C\), assuming no change in temperature and given the latent heat of vaporization to be 2450 kJ/kg?
Solution
199 J/K
91. Find the increase in entropy of 1.00 kg of liquid nitrogen that starts at its boiling temperature, boils, and warms to \(\displaystyle 20.0º C\) at constant pressure.
92. A large electrical power station generates 1000 MW of electricity with an efficiency of 35.0%.
(a) Calculate the heat transfer to the power station, \(\displaystyle Q_h\), in one day.
(b) How much heat transfer \(\displaystyle Q_c\) occurs to the environment in one day?
(c) If the heat transfer in the cooling towers is from \(\displaystyle 35.0º C\) water into the local air mass, which increases in temperature from \(\displaystyle 18.0º C\) to \(\displaystyle 20.0º C\), what is the total increase in entropy due to this heat transfer?
(d) How much energy becomes unavailable to do work because of this increase in entropy, assuming an \(\displaystyle 18.0º C\) lowest temperature? (Part of \(\displaystyle Q_c\) could be utilized to operate heat engines or for simply heating the surroundings, but it rarely is.)
Solution
(a) \(\displaystyle 2.47×10^{14}J\)
(b) \(\displaystyle 1.60×10^{14}J\)
(c) \(\displaystyle 2.85×10^{10}J/K\)
(d) \(\displaystyle 8.29×10^{12}J\)
93. (a) How much heat transfer occurs from 20.0 kg of \(\displaystyle 90.0º C\) water placed in contact with 20.0 kg of \(\displaystyle 10.0º C\) water, producing a final temperature of \(\displaystyle 50.0º C\)?
(b) How much work could a Carnot engine do with this heat transfer, assuming it operates between two reservoirs at constant temperatures of \(\displaystyle 90.0º C\) and \(\displaystyle 10.0º C\)?
(c) What increase in entropy is produced by mixing 20.0 kg of \(\displaystyle 90.0º C\) water with 20.0 kg of \(\displaystyle 10.0º C\) water?
(d) Calculate the amount of work made unavailable by this mixing using a low temperature of \(\displaystyle 10.0º C\), and compare it with the work done by the Carnot engine. Explicitly show how you follow the steps in the Problem-Solving Strategies for Entropy.
(e) Discuss how everyday processes make increasingly more energy unavailable to do work, as implied by this problem.
15.7: Statistical Interpretation of Entropy and the Second Law of Thermodynamics: The Underlying Explanation
94. Using Table, verify the contention that if you toss 100 coins each second, you can expect to get 100 heads or 100 tails once in \(\displaystyle 2×10^{22}\) calculate the time to two-digit accuracy.
Solution
It should happen twice in every \(\displaystyle 1.27×10^{30}s\) or once in every \(\displaystyle 6.35×10^{29}s\)
\(\displaystyle (6.35×10^{29}s)(\frac{1 h}{3600 s})=(\frac{1 d}{24 h})(\frac{1 y}{365.25 d})=2.0×10^{22}y\)
95. What percent of the time will you get something in the range from 60 heads and 40 tails through 40 heads and 60 tails when tossing 100 coins? The total number of microstates in that range is \(\displaystyle 1.22×10^{30}\). (Consult Table.)
96. (a) If tossing 100 coins, how many ways (microstates) are there to get the three most likely macrostates of 49 heads and 51 tails, 50 heads and 50 tails, and 51 heads and 49 tails?
(b) What percent of the total possibilities is this? (Consult Table.)
Solution
(a) \(\displaystyle 3.0×10^{29}\)
(b) 24%
97. (a) What is the change in entropy if you start with 100 coins in the 45 heads and 55 tails macrostate, toss them, and get 51 heads and 49 tails?
(b) What if you get 75 heads and 25 tails?
(c) How much more likely is 51 heads and 49 tails than 75 heads and 25 tails?
(d) Does either outcome violate the second law of thermodynamics?
98. (a) What is the change in entropy if you start with 10 coins in the 5 heads and 5 tails macrostate, toss them, and get 2 heads and 8 tails?
(b) How much more likely is 5 heads and 5 tails than 2 heads and 8 tails? (Take the ratio of the number of microstates to find out.)
(c) If you were betting on 2 heads and 8 tails would you accept odds of 252 to 45? Explain why or why not.
Solution
(a) \(\displaystyle −2.38×10^{–23}J/K\)
(b) 5.6 times more likely
(c) If you were betting on two heads and 8 tails, the odds of breaking even are 252 to 45, so on average you would break even. So, no, you wouldn’t bet on odds of 252 to 45.
99. (a) If you toss 10 coins, what percent of the time will you get the three most likely macrostates (6 heads and 4 tails, 5 heads and 5 tails, 4 heads and 6 tails)?
(b) You can realistically toss 10 coins and count the number of heads and tails about twice a minute. At that rate, how long will it take on average to get either 10 heads and 0 tails or 0 heads and 10 tails?
100. (a) Construct a table showing the macrostates and all of the individual microstates for tossing 6 coins. (Use Table as a guide.)
(b) How many macrostates are there?
(c) What is the total number of microstates?
(d) What percent chance is there of tossing 5 heads and 1 tail?
(e) How much more likely are you to toss 3 heads and 3 tails than 5 heads and 1 tail? (Take the ratio of the number of microstates to find out.)
Solution
(b) 7
(c) 64
(d) 9.38%
(e) 3.33 times more likely (20 to 6)
101. In an air conditioner, 12.65 MJ of heat transfer occurs from a cold environment in 1.00 h.
(a) What mass of ice melting would involve the same heat transfer?
(b) How many hours of operation would be equivalent to melting 900 kg of ice?
(c) If ice costs 20 cents per kg, do you think the air conditioner could be operated more cheaply than by simply using ice? Describe in detail how you evaluate the relative costs.
Contributors and Attributions
Paul Peter Urone (Professor Emeritus at California State University, Sacramento) and Roger Hinrichs (State University of New York, College at Oswego) with Contributing Authors: Kim Dirks (University of Auckland) and Manjula Sharma (University of Sydney). This work is licensed by OpenStax University Physics under a Creative Commons Attribution License (by 4.0).

