21.6: DC Circuits Containing Resistors and Capacitors
- Page ID
- 2693
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Learning Objectives
By the end of this section, you will be able to:
- Explain the importance of the time constant, τ, and calculate the time constant for a given resistance and capacitance.
- Explain why batteries in a flashlight gradually lose power and the light dims over time.
- Describe what happens to a graph of the voltage across a capacitor over time as it charges.
- Explain how a timing circuit works and list some applications.
- Calculate the necessary speed of a strobe flash needed to “stop” the movement of an object over a particular length.
When you use a flash camera, it takes a few seconds to charge the capacitor that powers the flash. The light flash discharges the capacitor in a tiny fraction of a second. Why does charging take longer than discharging? This question and a number of other phenomena that involve charging and discharging capacitors are discussed in this module.
RC Circuits
An \(RC\) circuit is one containing a resistor \(R\) and capacitor \(C\). The capacitor is an electrical component that stores electric charge.
Figure shows a simple \(RC\) circuit that employs a DC (direct current) voltage source. The capacitor is initially uncharged. As soon as the switch is closed, current flows to and from the initially uncharged capacitor. As charge increases on the capacitor plates, there is increasing opposition to the flow of charge by the repulsion of like charges on each plate.
In terms of voltage, this is because voltage across the capacitor is given by \(V_c = Q/C\), where \(Q\) is the amount of charge stored on each plate and \(C\) is the capacitance. This voltage opposes the battery, growing from zero to the maximum emf when fully charged. The current thus decreases from its initial value of \(I_9 = \frac{emf}{R}\) to zero as the voltage on the capacitor reaches the same value as the emf. When there is no current, there is no \(IR\) drop, and so the voltage on the capacitor must then equal the emf of the voltage source. This can also be explained with Kirchhoff’s second rule (the loop rule), discussed in Kirchhoff’s Rules, which says that the algebraic sum of changes in potential around any closed loop must be zero.
The initial current is \(I_0 = \frac{emf}{R}\), because all of the \(IR\) drop is in the resistance. Therefore, the smaller the resistance, the faster a given capacitor will be charged. Note that the internal resistance of the voltage source is included in \(R\), as are the resistances of the capacitor and the connecting wires. In the flash camera scenario above, when the batteries powering the camera begin to wear out, their internal resistance rises, reducing the current and lengthening the time it takes to get ready for the next flash.

Voltage on the capacitor is initially zero and rises rapidly at first, since the initial current is a maximum. Figure(b) shows a graph of capacitor voltage versus time (\(t\)) starting when the switch is closed at \(t - 0\). The voltage approaches emf asymptotically, since the closer it gets to emf the less current flows. The equation for voltage versus time when charging a capacitor \(C\) through a resistor \(R\), derived using calculus, is \[V = emf(1 - e^{-t/RC})(charging),\] where \(V\) is the voltage across the capacitor, emf is equal to the emf of the DC voltage source, and the exponential e = 2.718 … is the base of the natural logarithm. Note that the units of \(RC\) are seconds. We define \[\tau = RC,\] where \(\tau\) (the Greek letter tau) is called the time constant for an \(RC\) circuit. As noted before, a small resistance \(R\) allows the capacitor to charge faster. This is reasonable, since a larger current flows through a smaller resistance. It is also reasonable that the smaller the capacitor \(C\), the less time needed to charge it. Both factors are contained in \(\tau = RC\).
More quantitatively, consider what happens when \(t = \tau = RC\). Then the voltage on the capacitor is \[V = emf(1 - e^{-1}) = emf(1 - 0.368) = 0.632 \cdot emf.\]
This means that in the time \(\tau = RC\), the voltage rises to 0.632 of its final value. The voltage will rise 0.632 of the remainder in the next time \(\tau\) It is a characteristic of the exponential function that the final value is never reached, but 0.632 of the remainder to that value is achieved in every time \(\tau\). In just a few multiples of the time constant \(\tau\), then, the final value is very nearly achieved, as the graph in Figure(b) illustrates.
Discharging a Capacitor
Discharging a capacitor through a resistor proceeds in a similar fashion, as Figure illustrates. Initially, the current is \(I_9 - \frac{V_0}{R}\), driven by the initial voltage \(V_0\) on the capacitor. As the voltage decreases, the current and hence the rate of discharge decreases, implying another exponential formula for \(V\). Using calculus, the voltage \(V\) on a capacitor \(C\) being discharged through a resistor \(R\) is found to be \[V = V_0 e^{-t/RC} (discharging).\]
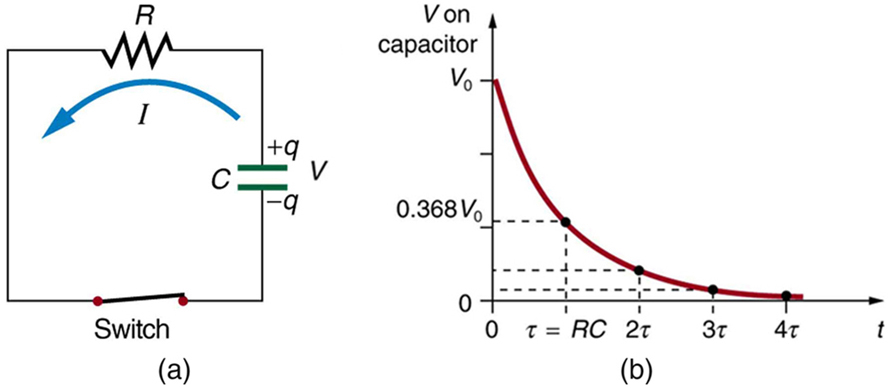
The graph in Figure(b) is an example of this exponential decay. Again, the time constant is \(\tau = RC\). A small resistance \(R\) allows the capacitor to discharge in a small time, since the current is larger. Similarly, a small capacitance requires less time to discharge, since less charge is stored. In the first time interval \(\tau = RC\) after the switch is closed, the voltage falls to 0.368 of its initial value, since \(V = V_0 \cdot e^{-1} = 0.368 V_0\).
During each successive time \(\tau\), the voltage falls to 0.368 of its preceding value. In a few multiples of \(\tau\), the voltage becomes very close to zero, as indicated by the graph in Figure(b).
Now we can explain why the flash camera in our scenario takes so much longer to charge than discharge; the resistance while charging is significantly greater than while discharging. The internal resistance of the battery accounts for most of the resistance while charging. As the battery ages, the increasing internal resistance makes the charging process even slower. (You may have noticed this.)
The flash discharge is through a low-resistance ionized gas in the flash tube and proceeds very rapidly. Flash photographs, such as in Figure, can capture a brief instant of a rapid motion because the flash can be less than a microsecond in duration. Such flashes can be made extremely intense.
During World War II, nighttime reconnaissance photographs were made from the air with a single flash illuminating more than a square kilometer of enemy territory. The brevity of the flash eliminated blurring due to the surveillance aircraft’s motion. Today, an important use of intense flash lamps is to pump energy into a laser. The short intense flash can rapidly energize a laser and allow it to reemit the energy in another form.

Example \(\PageIndex{1}\) : Integrated Concept Problem: Calculating Capacitor Size—Strobe Lights
High-speed flash photography was pioneered by Doc Edgerton in the 1930s, while he was a professor of electrical engineering at MIT. You might have seen examples of his work in the amazing shots of hummingbirds in motion, a drop of milk splattering on a table, or a bullet penetrating an apple (see Figure). To stop the motion and capture these pictures, one needs a high-intensity, very short pulsed flash, as mentioned earlier in this module.
Suppose one wished to capture the picture of a bullet (moving at \(5 \times 10^2 \, m/s\)) that was passing through an apple. The duration of the flash is related to the \(RC\) time constant \(\tau\). What size capacitor would one need in the \(RC\) circuit to succeed, if the resistance of the flash tube was \(10 \, \Omega\)? Assume the apple is a sphere with a diameter of \(8 \times 10^{-2} \, m\).
Strategy
We begin by identifying the physical principles involved. This example deals with the strobe light, as discussed above. Figure shows the circuit for this probe. The characteristic time \(\tau\) of the strobe is given as \(\tau = RC\).
Solution
We wish to find \(C\), but we don’t know \(\tau\). We want the flash to be on only while the bullet traverses the apple. So we need to use the kinematic equations that describe the relationship between distance \(x\), velocity \(v\), and time \(t\):
\[x = vt \, or \, t - \dfrac{x}{v}.\]
The bullet’s velocity is given as \(5 \times 10^2 \, m\), and the distance \(x\) is \(8 \times 10^{-2} \, m\). The traverse time, then, is
\[t = \dfrac{x}{v} = \dfrac{8.0 \times 10^{-2} \, m}{5.0 \times 10^2 \, m/s} = 1.6 \times 10^{-4} \, s.\]
We set this value for the crossing time \(t\) equal to \(\tau\). Therefore,
\[C = \dfrac{t}{R} = \dfrac{1.6 \times 10^{-4} \, s}{10.0 \, \Omega} = 16 \, \mu F.\]
(Note: Capacitance \(C\) is typically measured in farads, \(F\), defined as Coulombs per volt. From the equation, we see that \(C\) can also be stated in units of seconds per ohm.)
Discussion
The flash interval of \(160 \mu s\) (the traverse time of the bullet) is relatively easy to obtain today. Strobe lights have opened up new worlds from science to entertainment. The information from the picture of the apple and bullet was used in the Warren Commission Report on the assassination of President John F. Kennedy in 1963 to confirm that only one bullet was fired.
RC Circuits for Timing
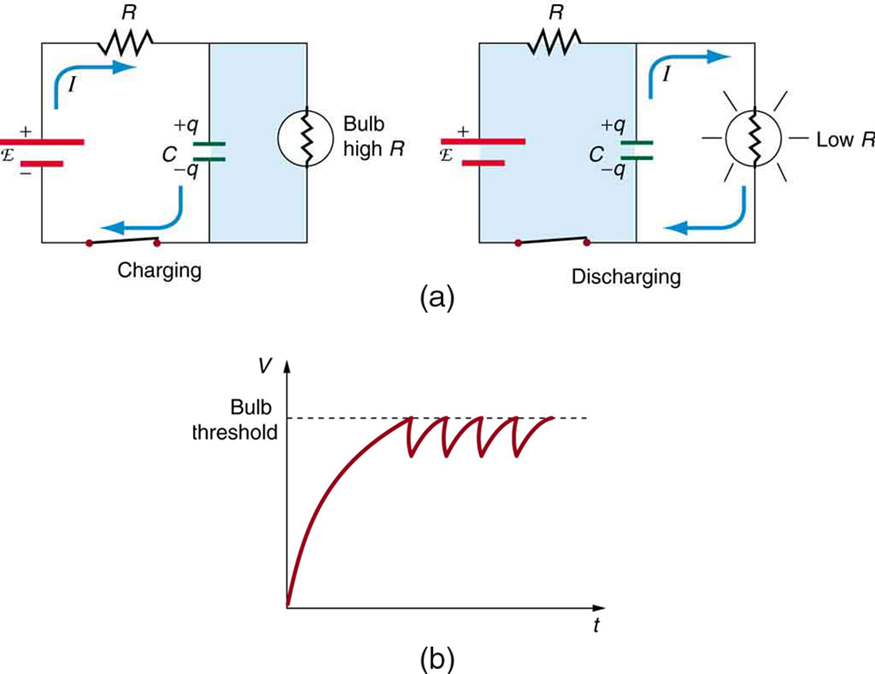
\(RC\) circuits are commonly used for timing purposes. A mundane example of this is found in the ubiquitous intermittent wiper systems of modern cars. The time between wipes is varied by adjusting the resistance in an \(RC\) circuit. Another example of an \(RC\) circuit is found in novelty jewelry, Halloween costumes, and various toys that have battery-powered flashing lights. (See Figure for a timing circuit.)
A more crucial use of \(RC\) circuits for timing purposes is in the artificial pacemaker, used to control heart rate. The heart rate is normally controlled by electrical signals generated by the sino-atrial (SA) node, which is on the wall of the right atrium chamber. This causes the muscles to contract and pump blood. Sometimes the heart rhythm is abnormal and the heartbeat is too high or too low.
The artificial pacemaker is inserted near the heart to provide electrical signals to the heart when needed with the appropriate time constant. Pacemakers have sensors that detect body motion and breathing to increase the heart rate during exercise to meet the body’s increased needs for blood and oxygen.
Example \(\PageIndex{2}\): Calculating Time: RC Circuit in a Heart Defibrillator
A heart defibrillator is used to resuscitate an accident victim by discharging a capacitor through the trunk of her body. A simplified version of the circuit is seen in Figure. (a) What is the time constant if an \(8.00 \, \mu F\) capacitor is used and the path resistance through her body is \(1 \times 10^3 \, \Omega\)? (b) If the initial voltage is 10.0 kV, how long does it take to decline to \(5 \times 10^2 \, V\)?
Strategy
Since the resistance and capacitance are given, it is straightforward to multiply them to give the time constant asked for in part (a). To find the time for the voltage to decline to \(5 \times 10^2 \, V\), we repeatedly multiply the initial voltage by 0.368 until a voltage less than or equal to \(5 \times 10^2 \, V\) is obtained. Each multiplication corresponds to a time of \(\tau\) seconds.
Solution for (a)
The time constant \(\tau\) is given by the equation \(\tau = RC\). Entering the given values for resistance and capacitance (and remembering that units for a farad can be expressed as \(s/\Omega\)) gives
\[\tau = RC = (1.00 \times 10^3 \, \Omega)(8.00 \, \mu F) = 8.00 \, ms.\]
Solution for (b)
In the first 8.00 ms, the voltage (10.0 kV) declines to 0.368 of its initial value. That is:
\[V = 0.368 V_0 = 3.680 \times 10^3 \, V \, at \, t = 8.00 \, ms.\]
(Notice that we carry an extra digit for each intermediate calculation.) After another 8.00 ms, we multiply by 0.368 again, and the voltage is
\[V' = 0.368 \, V\]
\[= (0.368)(3.680 \times 10^3 \, V)\]
\[=1.354 \times 10^3 \, V \, at \, t = 16.0 \, ms.\]
Similarly, after another 8.00 ms, the voltage is
\[V" = 0.368 \, V' = (0.368)(1.354 \times 10^3 \, V)\]
\[= 498 \, V \, at \, t = 24.0 \, ms.\]
Discussion
So after only 24.0 ms, the voltage is down to 498 V, or 4.98% of its original value.Such brief times are useful in heart defibrillation, because the brief but intense current causes a brief but effective contraction of the heart. The actual circuit in a heart defibrillator is slightly more complex than the one in Figure, to compensate for magnetic and AC effects that will be covered in Magnetism.
Exercise \(\PageIndex{1}\)
When is the potential difference across a capacitor an emf?
- Answer
-
Only when the current being drawn from or put into the capacitor is zero. Capacitors, like batteries, have internal resistance, so their output voltage is not an emf unless current is zero. This is difficult to measure in practice so we refer to a capacitor’s voltage rather than its emf. But the source of potential difference in a capacitor is fundamental and it is an emf.
PHET EXPLORATIONS: CIRCUIT CONSTRUCTION KIT (DC ONLY)
An electronics kit in your computer! Build circuits with resistors, light bulbs, batteries, and switches. Take measurements with the realistic ammeter and voltmeter. View the circuit as a schematic diagram, or switch to a life-like view.

Section Summary
- An \(RC\) circuit is one that has both a resistor and a capacitor.
- The time constant \(\tau\) for an \(RC\) circuit is \(\tau = RC\).
- When an initially uncharged \((V_0=0\) at \(t=0)\) capacitor in series with a resistor is charged by a DC voltage source, the voltage rises, asymptotically approaching the emf of the voltage source; as a function of time,
\[V=emf(1−e^{−t/RC})(charging).\] - Within the span of each time constant \(τ\), the voltage rises by 0.632 of the remaining value, approaching the final voltage asymptotically.
- If a capacitor with an initial voltage \(V_0\) is discharged through a resistor starting at \(t=0\), then its voltage decreases exponentially as given by
\[V=V_0e^{−t/RC}(discharging)\]. - In each time constant τ, the voltage falls by 0.368 of its remaining initial value, approaching zero asymptotically.
Glossary
- RC circuit
- a circuit that contains both a resistor and a capacitor
- capacitor
- an electrical component used to store energy by separating electric charge on two opposing plates
- capacitance
- the maximum amount of electric potential energy that can be stored (or separated) for a given electric potential


