29.1: Quantization of Energy
( \newcommand{\kernel}{\mathrm{null}\,}\)
Learning Objectives
By the end of this section, you will be able to:
- Explain Max Planck’s contribution to the development of quantum mechanics.
- Explain why atomic spectra indicate quantization.
Planck’s Contribution
Energy is quantized in some systems, meaning that the system can have only certain energies and not a continuum of energies, unlike the classical case. This would be like having only certain speeds at which a car can travel because its kinetic energy can have only certain values. We also find that some forms of energy transfer take place with discrete lumps of energy. While most of us are familiar with the quantization of matter into lumps called atoms, molecules, and the like, we are less aware that energy, too, can be quantized. Some of the earliest clues about the necessity of quantum mechanics over classical physics came from the quantization of energy.
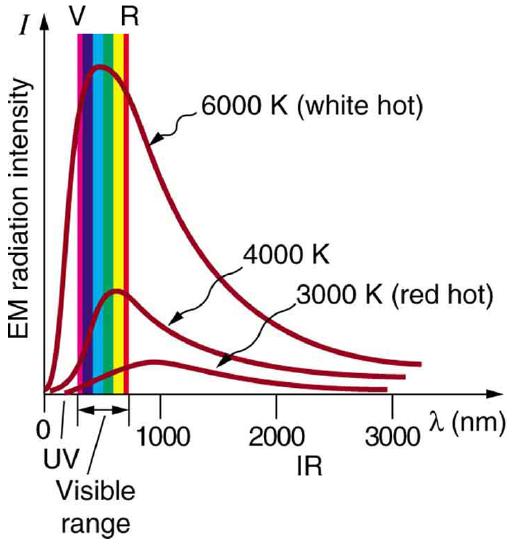
Where is the quantization of energy observed? Let us begin by considering the emission and absorption of electromagnetic (EM) radiation. The EM spectrum radiated by a hot solid is linked directly to the solid’s temperature (Figure 29.1.1) An ideal radiator is one that has an emissivity of 1 at all wavelengths and, thus, is jet black. Ideal radiators are therefore called blackbodies, and their EM radiation is called blackbody radiation. It was discussed that the total intensity of the radiation varies as T4, the fourth power of the absolute temperature of the body, and that the peak of the spectrum shifts to shorter wavelengths at higher temperatures. All of this seems quite continuous, but it was the curve of the spectrum of intensity versus wavelength that gave a clue that the energies of the atoms in the solid are quantized. In fact, providing a theoretical explanation for the experimentally measured shape of the spectrum was a mystery at the turn of the century. When this “ultraviolet catastrophe” was eventually solved, the answers led to new technologies such as computers and the sophisticated imaging techniques described in earlier chapters. Once again, physics as an enabling science changed the way we live.
The German physicist Max Planck (1858–1947) used the idea that atoms and molecules in a body act like oscillators to absorb and emit radiation. The energies of the oscillating atoms and molecules had to be quantized to correctly describe the shape of the blackbody spectrum. Planck deduced that the energy of an oscillator having a frequency f is given by
E=(n+12)hf.
Here n is any nonnegative integer (0, 1, 2, 3, …). The symbol h stands for Planck’s constant, given by
h=6.626×10−34J⋅s.
ΔE=hf.
It might be helpful to mention some macroscopic analogies of this quantization of energy phenomena. This is like a pendulum that has a characteristic oscillation frequency but can swing with only certain amplitudes. Quantization of energy also resembles a standing wave on a string that allows only particular harmonics described by integers. It is also similar to going up and down a hill using discrete stair steps rather than being able to move up and down a continuous slope. Your potential energy takes on discrete values as you move from step to step.
Using the quantization of oscillators, Planck was able to correctly describe the experimentally known shape of the blackbody spectrum. This was the first indication that energy is sometimes quantized on a small scale and earned him the Nobel Prize in Physics in 1918. Although Planck’s theory comes from observations of a macroscopic object, its analysis is based on atoms and molecules. It was such a revolutionary departure from classical physics that Planck himself was reluctant to accept his own idea that energy states are not continuous. The general acceptance of Planck’s energy quantization was greatly enhanced by Einstein’s explanation of the photoelectric effect (discussed in the next section), which took energy quantization a step further. Planck was fully involved in the development of both early quantum mechanics and relativity. He quickly embraced Einstein’s special relativity, published in 1905, and in 1906 Planck was the first to suggest the correct formula for relativistic momentum, p=γmu.

Note that Planck’s constant h is a very small number. So for an infrared frequency of 1014 being emitted by a blackbody, for example, the difference between energy levels is only ΔE=hf=(6.63×10−34J⋅s)(1014Hz)=6.63×10−20J, or about 0.4 eV. This 0.4 eV of energy is significant compared with typical atomic energies, which are on the order of an electron volt, or thermal energies, which are typically fractions of an electron volt. But on a macroscopic or classical scale, energies are typically on the order of joules. Even if macroscopic energies are quantized, the quantum steps are too small to be noticed. This is an example of the correspondence principle. For a large object, quantum mechanics produces results indistinguishable from those of classical physics.
Atomic Spectra
Now let us turn our attention to the emission and absorption of EM radiation by gases. The Sun is the most common example of a body containing gases emitting an EM spectrum that includes visible light. We also see examples in neon signs and candle flames. Studies of emissions of hot gases began more than two centuries ago, and it was soon recognized that these emission spectra contained huge amounts of information. The type of gas and its temperature, for example, could be determined. We now know that these EM emissions come from electrons transitioning between energy levels in individual atoms and molecules; thus, they are called atomic spectra. Atomic spectra remain an important analytical tool today. Figure 29.1.3 shows an example of an emission spectrum obtained by passing an electric discharge through a material. One of the most important characteristics of these spectra is that they are discrete. By this we mean that only certain wavelengths, and hence frequencies, are emitted. This is called a line spectrum. If frequency and energy are associated as ΔE=hf, the energies of the electrons in the emitting atoms and molecules are quantized. This is discussed in more detail later in this chapter.

It was a major puzzle that atomic spectra are quantized. Some of the best minds of 19th-century science failed to explain why this might be. Not until the second decade of the 20th century did an answer based on quantum mechanics begin to emerge. Again a macroscopic or classical body of gas was involved in the studies, but the effect, as we shall see, is due to individual atoms and molecules.
PHET EXPLORATIONS: MODELS OF THE HYDROGEN ATOM
How did scientists figure out the structure of atoms without looking at them? Try out different models by shooting light at the atom. Check how the prediction of the model matches the experimental results.
![]()
Summary
- The first indication that energy is sometimes quantized came from blackbody radiation, which is the emission of EM radiation by an object with an emissivity of 1.
- Planck recognized that the energy levels of the emitting atoms and molecules were quantized, with only the allowed values of E=(n+12)hf, where n is any non-negative integer (0, 1, 2, 3, …).
- h is Planck’s constant, whose value is h=6.626×10−34J⋅s.
- Thus, the oscillatory absorption and emission energies of atoms and molecules in a blackbody could increase or decrease only in steps of size ΔE=hf where f is the frequency of the oscillatory nature of the absorption and emission of EM radiation.
- Another indication of energy levels being quantized in atoms and molecules comes from the lines in atomic spectra, which are the EM emissions of individual atoms and molecules.
Glossary
- blackbody
- an ideal radiator, which can radiate equally well at all wavelengths
- blackbody radiation
- the electromagnetic radiation from a blackbody
- Planck’s constant
- 6.626×10−34J⋅s
- atomic spectra
- the electromagnetic emission from atoms and molecules


