34.E: Frontiers of Physics (Exercises)

Conceptual Questions

34.1: Cosmology and Particle Physics

1. Explain why it only appears that we are at the center of expansion of the universe and why an observer in another galaxy would see the same relative motion of all but the closest galaxies away from her.

2. If there is no observable edge to the universe, can we determine where its center of expansion is? Explain.

3. If the universe is infinite, does it have a center? Discuss.

4. Another known cause of red shift in light is the source being in a high gravitational field. Discuss how this can be eliminated as the source of galactic red shifts, given that the shifts are proportional to distance and not to the size of the galaxy.

5. If some unknown cause of red shift—such as light becoming “tired” from traveling long distances through empty space—is discovered, what effect would there be on cosmology?

6. Olbers’s paradox poses an interesting question: If the universe is infinite, then any line of sight should eventually fall on a star’s surface. Why then is the sky dark at night? Discuss the commonly accepted evolution of the universe as a solution to this paradox.

7. If the cosmic microwave background radiation (CMBR) is the remnant of the Big Bang’s fireball, we expect to see hot and cold regions in it. What are two causes of these wrinkles in the CMBR? Are the observed temperature variations greater or less than originally expected?

8. The decay of one type of \(\displaystyle K\)-meson is cited as evidence that nature favors matter over antimatter. Since mesons are composed of a quark and an antiquark, is it surprising that they would preferentially decay to one type over another? Is this an asymmetry in nature? Is the predominance of matter over antimatter an asymmetry?

9. Distances to local galaxies are determined by measuring the brightness of stars, called Cepheid variables, that can be observed individually and that have absolute brightnesses at a standard distance that are well known. Explain how the measured brightness would vary with distance as compared with the absolute brightness.

10. Distances to very remote galaxies are estimated based on their apparent type, which indicate the number of stars in the galaxy, and their measured brightness. Explain how the measured brightness would vary with distance. Would there be any correction necessary to compensate for the red shift of the galaxy (all distant galaxies have significant red shifts)? Discuss possible causes of uncertainties in these measurements.

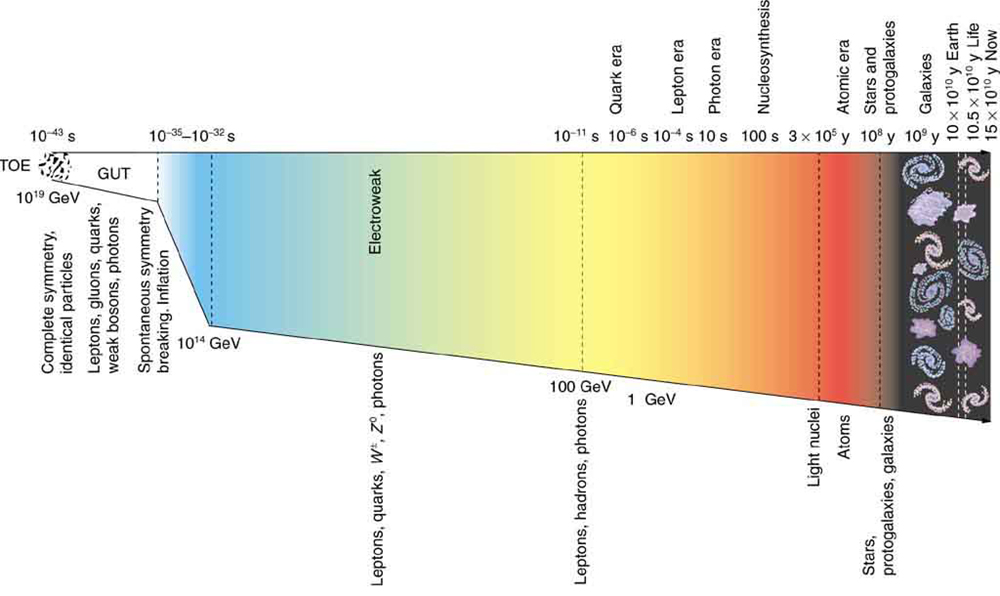
11. If the smallest meaningful time interval is greater than zero, will the lines in Figure ever meet?

34.2: General Relativity and Quantum Gravity

12. Quantum gravity, if developed, would be an improvement on both general relativity and quantum mechanics, but more mathematically difficult. Under what circumstances would it be necessary to use quantum gravity? Similarly, under what circumstances could general relativity be used? When could special relativity, quantum mechanics, or classical physics be used?

13. Does observed gravitational lensing correspond to a converging or diverging lens? Explain briefly.

14. Suppose you measure the red shifts of all the images produced by gravitational lensing, such as in Figure.You find that the central image has a red shift less than the outer images, and those all have the same red shift. Discuss how this not only shows that the images are of the same object, but also implies that the red shift is not affected by taking different paths through space. Does it imply that cosmological red shifts are not caused by traveling through space (light getting tired, perhaps)?

15. What are gravitational waves, and have they yet been observed either directly or indirectly?

16. Is the event horizon of a black hole the actual physical surface of the object?

17. Suppose black holes radiate their mass away and the lifetime of a black hole created by a supernova is about 1067 years. How does this lifetime compare with the accepted age of the universe? Is it surprising that we do not observe the predicted characteristic radiation?

34.4: Dark Matter and Closure

18. Discuss the possibility that star velocities at the edges of galaxies being greater than expected is due to unknown properties of gravity rather than to the existence of dark matter. Would this mean, for example, that gravity is greater or smaller than expected at large distances? Are there other tests that could be made of gravity at large distances, such as observing the motions of neighboring galaxies?

19. How does relativistic time dilation prohibit neutrino oscillations if they are massless?

20. If neutrino oscillations do occur, will they violate conservation of the various lepton family numbers \(\displaystyle (L_e, L_μ,\) and \(\displaystyle L_τ)\)? Will neutrino oscillations violate conservation of the total number of leptons?

21. Lacking direct evidence of WIMPs as dark matter, why must we eliminate all other possible explanations based on the known forms of matter before we invoke their existence?

34.5: Complexity and Chaos

22. Must a complex system be adaptive to be of interest in the field of complexity? Give an example to support your answer.

23. State a necessary condition for a system to be chaotic.

34.6: High-temperature Superconductors

24. What is critical temperature \(\displaystyle T_c\)? Do all materials have a critical temperature? Explain why or why not.

25. Explain how good thermal contact with liquid nitrogen can keep objects at a temperature of 77 K (liquid nitrogen’s boiling point at atmospheric pressure).

26. Not only is liquid nitrogen a cheaper coolant than liquid helium, its boiling point is higher (77 K vs. 4.2 K). How does higher temperature help lower the cost of cooling a material? Explain in terms of the rate of heat transfer being related to the temperature difference between the sample and its surroundings.

34.7: Some Questions We Know to Ask

27. For experimental evidence, particularly of previously unobserved phenomena, to be taken seriously it must be reproducible or of sufficiently high quality that a single observation is meaningful. Supernova 1987A is not reproducible. How do we know observations of it were valid? The fifth force is not broadly accepted. Is this due to lack of reproducibility or poor-quality experiments (or both)? Discuss why forefront experiments are more subject to observational problems than those involving established phenomena.

28. Discuss whether you think there are limits to what humans can understand about the laws of physics. Support your arguments.

Problems & Exercises

34.1: Cosmology and Particle Physics

29. Find the approximate mass of the luminous matter in the Milky Way galaxy, given it has approximately \(\displaystyle 10^{11}\) stars of average mass 1.5 times that of our Sun.

Solution
\(\displaystyle 3×10^{41}kg\)

30. Find the approximate mass of the dark and luminous matter in the Milky Way galaxy. Assume the luminous matter is due to approximately 1011 stars of average mass 1.5 times that of our Sun, and take the dark matter to be 10 times as massive as the luminous matter.

31. (a) Estimate the mass of the luminous matter in the known universe, given there are \(\displaystyle 10^{11}\) galaxies, each containing \(\displaystyle 10^{11}\) stars of average mass 1.5 times that of our Sun.

(b) How many protons (the most abundant nuclide) are there in this mass?

(c) Estimate the total number of particles in the observable universe by multiplying the answer to (b) by two, since there is an electron for each proton, and then by \(\displaystyle 10^9\), since there are far more particles (such as photons and neutrinos) in space than in luminous matter.

Solution
(a) \(\displaystyle 3×10^{52}kg\)
(b) \(\displaystyle 2×10^{79}\)
(c) \(\displaystyle 4×10^{88}\)

32. If a galaxy is 500 Mly away from us, how fast do we expect it to be moving and in what direction?

33. On average, how far away are galaxies that are moving away from us at 2.0% of the speed of light?

Solution
0.30 Gly

34. Our solar system orbits the center of the Milky Way galaxy. Assuming a circular orbit 30,000 ly in radius and an orbital speed of 250 km/s, how many years does it take for one revolution? Note that this is approximate, assuming constant speed and circular orbit, but it is representative of the time for our system and local stars to make one revolution around the galaxy.

35. (a) What is the approximate speed relative to us of a galaxy near the edge of the known universe, some 10 Gly away?

(b) What fraction of the speed of light is this? Note that we have observed galaxies moving away from us at greater than \(\displaystyle 0.9c\).

Solution
(a) \(\displaystyle 2.0×10^5km/s\)
(b) 0.67c

36. (a) Calculate the approximate age of the universe from the average value of the Hubble constant, \(\displaystyle H_0=20km/s⋅Mly\). To do this, calculate the time it would take to travel 1 Mly at a constant expansion rate of 20 km/s.

(b) If deceleration is taken into account, would the actual age of the universe be greater or less than that found here? Explain.

37. Assuming a circular orbit for the Sun about the center of the Milky Way galaxy, calculate its orbital speed using the following information: The mass of the galaxy is equivalent to a single mass \(\displaystyle 1.5×10^{11}\) times that of the Sun (or \(\displaystyle 3×10^{41}kg\)), located 30,000 ly away.

Solution
\(\displaystyle 2.7×10^5m/s\)

38. (a) What is the approximate force of gravity on a 70-kg person due to the Andromeda galaxy, assuming its total mass is \(\displaystyle 10^{13}\) that of our Sun and acts like a single mass 2 Mly away?

(b) What is the ratio of this force to the person’s weight? Note that Andromeda is the closest large galaxy.

39. Andromeda galaxy is the closest large galaxy and is visible to the naked eye. Estimate its brightness relative to the Sun, assuming it has luminosity \(\displaystyle 10^{12}\) times that of the Sun and lies 2 Mly away.

Solution
\(\displaystyle 6×10^{−11}\) (an overestimate, since some of the light from Andromeda is blocked by gas and dust within that galaxy)

40. (a) A particle and its antiparticle are at rest relative to an observer and annihilate (completely destroying both masses), creating two γ rays of equal energy. What is the characteristic γ-ray energy you would look for if searching for evidence of proton-antiproton annihilation? (The fact that such radiation is rarely observed is evidence that there is very little antimatter in the universe.)

(b) How does this compare with the 0.511-MeV energy associated with electron-positron annihilation?

41. The average particle energy needed to observe unification of forces is estimated to be \(\displaystyle 10^{19}GeV.\)

(a) What is the rest mass in kilograms of a particle that has a rest mass of \(\displaystyle 10^{19}GeV/c^2\)?

(b) How many times the mass of a hydrogen atom is this?

Solution
(a) \(\displaystyle 2×10^{−8}kg\)
(b) \(\displaystyle 1×10^{19}\)

42. The peak intensity of the CMBR occurs at a wavelength of 1.1 mm.

(a) What is the energy in eV of a 1.1-mm photon?

(b) There are approximately \(\displaystyle 10^9\) photons for each massive particle in deep space. Calculate the energy of \(\displaystyle 10^9\) such photons.

(c) If the average massive particle in space has a mass half that of a proton, what energy would be created by converting its mass to energy?

(d) Does this imply that space is “matter dominated”? Explain briefly.

43. (a) What Hubble constant corresponds to an approximate age of the universe of \(\displaystyle 10^{10}y\)? To get an approximate value, assume the expansion rate is constant and calculate the speed at which two galaxies must move apart to be separated by 1 Mly (present average galactic separation) in a time of \(\displaystyle 10^{10}y\).

(b) Similarly, what Hubble constant corresponds to a universe approximately \(\displaystyle 2×10^{10}-y\) old?

Solution
(a) 30km/s⋅Mly
(b) 15km/s⋅Mly

44. Show that the velocity of a star orbiting its galaxy in a circular orbit is inversely proportional to the square root of its orbital radius, assuming the mass of the stars inside its orbit acts like a single mass at the center of the galaxy. You may use an equation from a previous chapter to support your conclusion, but you must justify its use and define all terms used.

45. The core of a star collapses during a supernova, forming a neutron star. Angular momentum of the core is conserved, and so the neutron star spins rapidly. If the initial core radius is \(\displaystyle 5.0×10^5km\) and it collapses to 10.0 km, find the neutron star’s angular velocity in revolutions per second, given the core’s angular velocity was originally 1 revolution per 30.0 days.

Solution
960 rev/s

46. Using data from the previous problem, find the increase in rotational kinetic energy, given the core’s mass is 1.3 times that of our Sun. Where does this increase in kinetic energy come from?

47. Distances to the nearest stars (up to 500 ly away) can be measured by a technique called parallax, as shown in Figure. What are the angles \(\displaystyle θ_1\) and \(\displaystyle θ_2\) relative to the plane of the Earth’s orbit for a star 4.0 ly directly above the Sun?

Solution
\(\displaystyle 89.999773º\) (many digits are used to show the difference between \(\displaystyle 90º\))

48. (a) Use the Heisenberg uncertainty principle to calculate the uncertainty in energy for a corresponding time interval of \(\displaystyle 10^{−43}s\).

(b) Compare this energy with the \(\displaystyle 10^{19}GeV\) unification-of-forces energy and discuss why they are similar.

49. Construct Your Own Problem

Consider a star moving in a circular orbit at the edge of a galaxy. Construct a problem in which you calculate the mass of that galaxy in kg and in multiples of the solar mass based on the velocity of the star and its distance from the center of the galaxy.

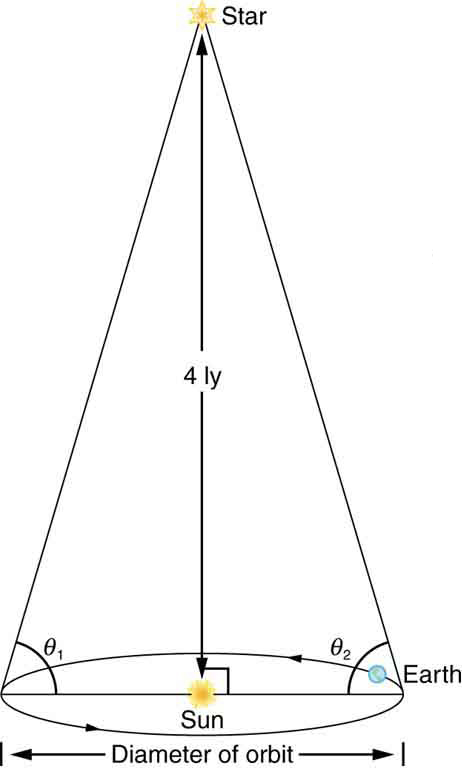
Distances to nearby stars are measured using triangulation, also called the parallax method. The angle of line of sight to the star is measured at intervals six months apart, and the distance is calculated by using the known diameter of the Earth’s orbit. This can be done for stars up to about 500 ly away.

34.2: General Relativity and Quantum Gravity

50. What is the Schwarzschild radius of a black hole that has a mass eight times that of our Sun? Note that stars must be more massive than the Sun to form black holes as a result of a supernova.

Solution
23.6 km

51. Black holes with masses smaller than those formed in supernovas may have been created in the Big Bang. Calculate the radius of one that has a mass equal to the Earth’s.

52. Supermassive black holes are thought to exist at the center of many galaxies.

(a) What is the radius of such an object if it has a mass of \(\displaystyle 10^9\) Suns?

(b) What is this radius in light years?

Solution
(a) \(\displaystyle 2.95×10^{12}m\)
(b) \(\displaystyle 3.12×10^{−4}ly\)

53. Construct Your Own Problem

Consider a supermassive black hole near the center of a galaxy. Calculate the radius of such an object based on its mass. You must consider how much mass is reasonable for these large objects, and which is now nearly directly observed. (Information on black holes posted on the Web by NASA and other agencies is reliable, for example.)

34.3: Superstrings

54. The characteristic length of entities in Superstring theory is approximately \(\displaystyle 10^{−35}m\).

(a) Find the energy in GeV of a photon of this wavelength.

(b) Compare this with the average particle energy of \(\displaystyle 10^{19}GeV\) needed for unification of forces.

Solution
(a) \(\displaystyle 1×10^{20}\)
(b) 10 times greater

34.4: Dark Matter and Closure

55. If the dark matter in the Milky Way were composed entirely of MACHOs (evidence shows it is not), approximately how many would there have to be? Assume the average mass of a MACHO is 1/1000 that of the Sun, and that dark matter has a mass 10 times that of the luminous Milky Way galaxy with its \(\displaystyle 10^{11}\) stars of average mass 1.5 times the Sun’s mass.

Solution
\(\displaystyle 1.5×10^{15}\)

56. The critical mass density needed to just halt the expansion of the universe is approximately \(\displaystyle 10^{−26}kg/m^3\).

(a) Convert this to \(\displaystyle eV/c^2⋅m^3\).

(b) Find the number of neutrinos per cubic meter needed to close the universe if their average mass is \(\displaystyle 7eV/c^2\) and they have negligible kinetic energies.

57. Assume the average density of the universe is 0.1 of the critical density needed for closure. What is the average number of protons per cubic meter, assuming the universe is composed mostly of hydrogen?

Solution
\(\displaystyle 0.6m^{−3}\)

68. To get an idea of how empty deep space is on the average, perform the following calculations:

(a) Find the volume our Sun would occupy if it had an average density equal to the critical density of \(\displaystyle 10^{−26}kg/m^3\) thought necessary to halt the expansion of the universe.

(b) Find the radius of a sphere of this volume in light years.

(c) What would this radius be if the density were that of luminous matter, which is approximately 5% that of the critical density?

(d) Compare the radius found in part (c) with the 4-ly average separation of stars in the arms of the Milky Way.

34.6: High-temperature Superconductors

69. A section of superconducting wire carries a current of 100 A and requires 1.00 L of liquid nitrogen per hour to keep it below its critical temperature. For it to be economically advantageous to use a superconducting wire, the cost of cooling the wire must be less than the cost of energy lost to heat in the wire. Assume that the cost of liquid nitrogen is $0.30 per liter, and that electric energy costs $0.10 per kW·h. What is the resistance of a normal wire that costs as much in wasted electric energy as the cost of liquid nitrogen for the superconductor?

Solution
0.30 Ω

Contributors and Attributions

• Paul Peter Urone (Professor Emeritus at California State University, Sacramento) and Roger Hinrichs (State University of New York, College at Oswego) with Contributing Authors: Kim Dirks (University of Auckland) and Manjula Sharma (University of Sydney). This work is licensed by OpenStax University Physics under a Creative Commons Attribution License (by 4.0).