8.6: Acceleration During a Skydive
( \newcommand{\kernel}{\mathrm{null}\,}\)
Acceleration
After the air resistance becomes large enough to balance out a skydiver’s weight, they will have no net force. From Newton's First Law we already know that an object’s inertia prevents a change in velocity unless it experience a net force, so from that point when the forces are balanced and onward, the skydiver continues at a constant velocity until they open their parachute.
During the initial part of skydive, before the drag force is large enough to balance out the weight, there is a net force so their velocity does change. The rate at which the velocity changes is known as the acceleration. Note that students often confuse velocity and acceleration because they are both rates of change, so to be specific: velocity defines the rate at which the position is changing and acceleration defines the rate at which the velocity is changing. We can calculate the average acceleration (a) during a certain time interval (Δt) by subtracting the initial velocity (vi) from the final velocity (vf) to get the change in velocity (Δv) and then dividing by time interval (Δt):
(1)
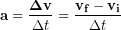
Everyday Example
 and
and  .
.
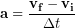
Inserting our values:
![]()
The two negatives in front of the 54 m/s make a positive, and then we calculate a value.
![]()
We now get a chance to see that the units of acceleration are m/s/s or equivalently m/s2
Acceleration Direction
The direction of acceleration depends on the direction of the change in velocity. If the velocity becomes more negative, then acceleration must be negative. This is the case for our skydiver during the first part of the jump; their speed is increasing in the negative direction, so their velocity is becoming more negative, so their acceleration is negative. Conversely, if an object moves in the negative direction, but slows down, the acceleration is positive, even though the velocity is still negative! This was the case for our skydiver just after opening their parachute, when they still moved downward, but were slowing down. Slowing down in the negative direction means the velocity is becoming less negative, so the acceleration must be positive. All of the possible combinations of velocity direction and speed change and the resulting acceleration are summarized in the following chart:
| Initial direction of motion ( initial velocity direction) | Speed change | Direction of Acceleration |
| positive | speeding up | positive |
| positive | slowing down | negative |
| negative | speeding up | negative |
| negative | slowing down | positive |
Reinforcement Exercises
A car is moving in the positive direction and slams on the brakes. What direction is the acceleration?
A car is moving in the negative direction and slams on the brakes. What direction is the acceleration?
A car is moving in the negative direction and speeding up. What direction is the acceleration?
Accelerating the Body
Newton's First Law tells us that we need a net force in order to create an acceleration. As you might expect, a larger net force will cause a larger acceleration, but the more matter you are trying to accelerate the larger force will be required. Newton's Second Law summarizes all of that into a single equation relating the net force, mass, and acceleration:
(2)
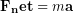
We can think of Newton’s Second Law in terms of the acceleration instead:
(3)
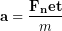
Now we see that larger net forces create larger accelerations and larger masses reduce the size of the acceleration. In fact, an object’s mass is a direct measure of an objects resistance to changing its motion, or its inertia.
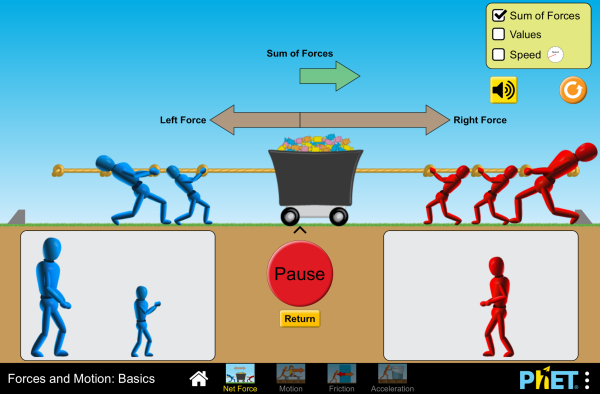
Check out this simulation to see how forces combine to create net forces and accelerations:
Reinforcement Exercises
You slide a box across the floor by applying a 220 N force to the right. Kinetic friction applies a reactive 170 N force on the box to the left.
What is the size and direction of the net force on the box?
The box has a mass of 25 kg. What is the size and direction of the acceleration on the box?
The box is not accelerating in the vertical direction, so what is the net vertical force? [Hint: Forces in different dimensions (vertical and horizontal) don’t affect one another and Newton's Second Law applies separately to each dimension.]
How big is the normal force on the box?
What is the value of the kinetic friction coefficient?
It’s an interesting quirk of our universe that the same property of an object, specifically its mass, determines both the force of gravity on it and its resistance to accelerations, or inertia. Said another way, the inertial mass and the gravitational mass are equivalent. This result produces some interesting phenomena, as we will see in the following example.
Everyday Example
Let’s calculate the initial acceleration of our skydiver the moment they jump. At this moment they have the force of gravity pulling them down, but they have not yet gained any speed, so the air resistance (drag force) is zero. The net force is then just gravity, because it is the only force. Starting with Newton's Second Law:
(4)
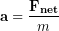
And inserting our known formula for calculating force of gravity near the surface of Earth and including a negative sign because down is our negative direction, (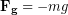 ):
):
(5)
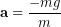
We see that the mass cancels out,
(6)
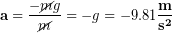
We see that our acceleration is negative, which makes sense because the acceleration is downward. We also see that the size of the acceleration is g = 9.81 m/s2. We have just shown that in the absence of air resistance, all objects falling near the surface of Earth will experience an acceleration equal in size to g = 9.81 m/s2, regardless of their mass and weight.
In the previous example we found that our skydiver has an initial acceleration of g = 9.81 m/s2, but as they gain speed the drag force begins to push back and their acceleration decreases (they are still gaining speed each second, they are just not gaining as much speed each second as they were at the start). Finally the drag force becomes as large as the weight and their acceleration becomes zero, and they have reached terminal speed. In the next chapter we will work on understanding how to use velocity and acceleration to predict the position of objects, including our skydiver, and how graphing the position, velocity, and acceleration can help us do so.