9.7: Locomotion
( \newcommand{\kernel}{\mathrm{null}\,}\)
The astronaut in the video above pushed against the wall (using a single human hair) and the wall pushed back against her according to Newton's Third Law. She was not contacting any other surfaces and the speed was small enough that drag force was not a factor, therefore the wall pushing on her caused a net force on her body, so she accelerated according to Newton's Second Law.
Reinforcement Activity
If the astronaut in the previous video pushes against the wall with 3 N of force, what is the force applied back to her by the wall?
If the astronaut has a mass of 60 kg, what is her acceleration?
It’s not difficult to image the astronaut pushing with enough force to break the hair. In similar fashion, the body is capable of generating forces large enough to cause injury to body tissues much stronger than hair while in the process of generating motion. In order to study those types of injuries we need to look at how the body moves in greater detail.
In general, the capacity for generating movement, or locomotion is based on a combination of Newton's Third and Second Laws. Body locomotion occurs when the body initiates muscle contraction in order to apply a force against another object, such as the floor or the wall. The other object then applies an equal and opposite reaction force against the body, according to Newton’s Third Law. That reaction force acting on the body adds together with all of the other forces on the body to determine the net force. The net force causes the body to accelerate as dictated by the size of the net force and body mass according to Newton's Second Law.
Everyday Example: Jumping
When a person stands still on flat ground, they are in static equilibrium and the normal force pushing up from the ground is equal to their weight. In order to jump, the muscles of the leg contract to push even harder down against the floor. This downward push results in an equal reactive normal force from the floor, so that now the normal force is greater than body weight, resulting in a net force. Now with an upward net force, the body will experience an upward acceleration, which increases upward velocity (starting from zero). The following graph of the normal force on person was created by jumping and landing on a force plate, which is essentially a extra-tough digital scale that records the normal force that it provides over time.

Normal force from the ground on a person during a jump as recorded by a digital force plate during the experiment described in the following text.
First the jumper steps on the force plate and it reads their weight of about 800 N. Then the plate reading dips a couple hundred Newtons because the upward normal force is reduced as they drop down into a crouch, which makes sense because they must accelerate downward to drop down. Next the force peaks to near 1700 N they push off hard to accelerate upward to stop their downward motion and initiate upward motion, here we see the normal force is greater than the weight. The normal force drops to zero as the body leaves contact with the ground. While in the air gravity provides the net downward force so the acceleration is downward, and the body’s upward velocity slows. (After leaving the ground the acceleration is –g= –9.8 m/s/s). The body eventually turns around as the upward velocity reaches zero, and then begins to move back toward the ground. Landing requires an upward acceleration to stop the downward velocity, so a large upward normal force of over 2500 N is produced. The jumper is attempting a “soft landing” and so continues into a crouching position during landing, which causes another couple hundred Newton dip in the normal force at the end of landing. Finally, the normal force equals weight again after landing is complete. The next chapter will talk more about “soft landings” and other methods of injury prevention.
Every Day Examples: Walking and Running
When walking or running you push horizontally against the floor and the floor pushes back, providing you with the net force necessary to create acceleration. Walking at constant average speed is achieved by alternating of forward acceleration caused when the floor pushes forward on your back foot, and backward acceleration caused by the floor pushing back on your front foot. These accelerations cancel each other out on average to create constant speed, but if you use a sensor capable of taking several measurements per second, then you can see the changing instantaneous speed reveals the oscillatory nature of walking motion:

Acceleration vs. time curve for a person walking.
An initial positive acceleration corresponds with the change in velocity away from zero during the first step. Afterward, constant walking motion results in acceleration that oscillates from positive to negative and averages out to zero.

Velocity vs. time curve for a person walking.
The oscillating accelerations result in a velocity that alternates between slowing down and speeding up, however we can see that the velocity stays positive so you are always making progress in the direction you intend to walk. We also see that over a full gait cycle average velocity is constant, near 0.4 m/s for this example, which agrees with the zero average acceleration in the previous graph.
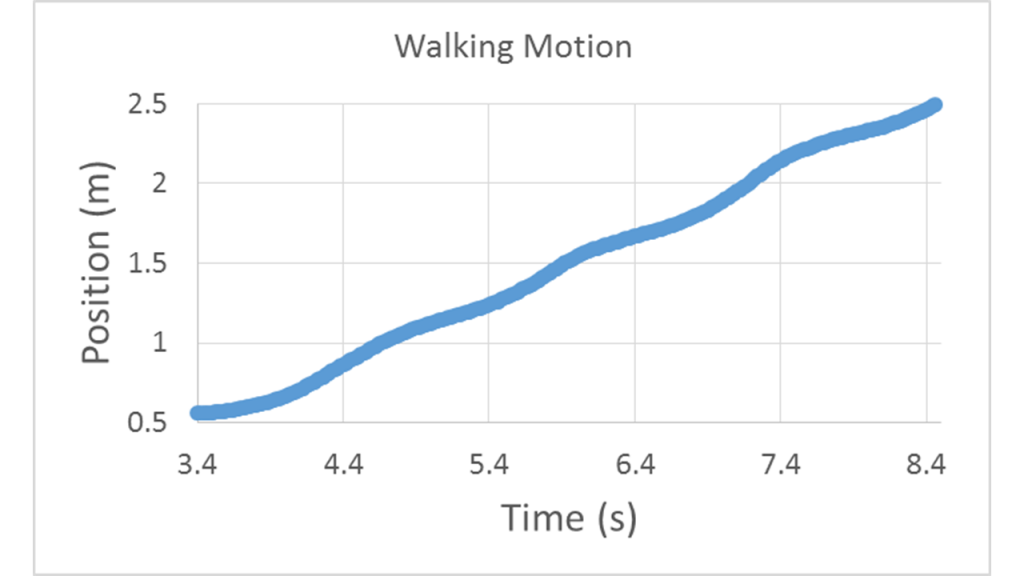
Position vs. time curve of a person walking.
As you make progress, the position increases roughly linearly with an average slope equal to your constant average velocity, in this case 0.4 m/s. However the oscillations in the instantaneous velocity are noticeable as slight variations in the slope of the position graph.
Everyday Example: Driving
In order for your car to accelerate along a flat road, it must have a net horizontal force. What force acts on your car to provide this net force? Remember the force must be on the car from another object, the car can’t put a net force on itself (so the answer can’t be the engine or any part of the car). Gravity and normal force are external forces on a car, but those forces act vertically and cannot contribute to a horizontal acceleration. The force that acts on your car in the horizontal direction is friction. When the tires attempt to rotate, they push against the ground via friction, and the ground pushes back with an equal reactionary friction force, according to Newton’s Third Law. Then, according to Newton’s Second Law, that friction force acting on the car accelerates the car. The purpose of the throttle, engine, and drive train is to cause the tires to push back on the road in order to receive the forward push from the road in return.

Locomotion in cars is created by the reactionary friction force on the car tires from the road in response to the friction force from the tires on the road. Forward acceleration occurs when the force on the tires from the road is larger than the drag force, providing a net force in the forward direction. Image adapted from Fifth generation Chevrolet Malibu on Interstate 85 in Durham, North Carolina by Ildar Sagdejev (Specious) via wikimedia commons
Also, your car pushes on the air to move it out the way, so according to Newton’s 3rd Law, the air puts a drag force back on your car. When the drag force and the friction force on the car are equal the car reaches a sort of terminal velocity. If you want the car to go faster, you need to increase the friction force on the car from the road, which you achieve by increasing how hard the tires push back against the road via the throttle, engine, and drive train successively.
- Adapted from Fifth generation Chevrolet Malibu on Interstate 85 in Durham, North Carolina by Ildar Sagdejev (Specious) - Own work, CC BY-SA 3.0, via wikimedia commons↵



