10.9: Efficiency of the Human Body

The Energetic Functions of the Body

We have learned so far that your body takes in chemical potential energy, and then does work to convert that into mechanical energy for locomotion, chemical potential energy for storage, and thermal energy. The following diagram summarizes the basic energetic functioning in the human body. (Electric potential energy is important to nerve conduction and other processes in the body, and we have mentioned that chemical potential energy is actually a form of electric potential energy, but we will not specifically discuss electric potential energy in this textbook.)

The most basic functions of the human body mapped to the main concepts covered in this textbook.

The body is capable of storing chemical potential energy and thermal energy internally. Remembering that thermal energy is just the kinetic energy of atoms and molecules, we recognize that these two types of energy are stored microscopically and internal to the body. Therefore, we often lump these two types of microscopic energy into the internal energy (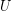). When on object is warmer then its surroundings then thermal energy will be transferred from object to surroundings, but if the object is cooler than its surroundings then thermal energy will transferred into the object from its surroundings. The amount of thermal energy exchanged due to temperature differences is often called heat (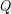). When heat is transferred out of the body to the environment, we say call this exhaust heat, as indicated in the previous figure. We will learn more about how temperature and heat transfer are related in the next unit.

The First Law of Thermodynamics

The Principle of Conservation of Energy states that energy cannot be created or destroyed. Therefore, if the body does useful work to transfer mechanical energy to its surroundings (), or transfer thermal energy to the environment as heat, then that energy must have come out of the body’s internal energy. We observe this in nature as the First Law of Thermodynamics:

(1)

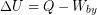
Your body uses chemical potential energy stored internally to do work, and that process also generates thermal energy, which you release as exhaust heat. The internal combustion engines that power most cars operate in similar fashion by converting chemical potential energy in fuel to thermal energy via combustion, then converting some of the thermal energy into useful work and some into exhaust heat. Your body is capable of releasing the chemical potential energy in your food without combustion, which is good, because you are not capable of using thermal energy your from yourinternal energy to do work. Machines that can use thermal energy to do work, such as a combustion engine, are known as heat engines. Heat engines are still governed by the First Law of Thermodynamics, so any exhaust heat must have been thermal energy that was not used to do work. The thermal energy input that can be used to do work rather than wasted as exhaust heat determines the efficiency of the heat engine.

Reinforcement Exercises

You apply a 50 N force in order to slide an object 3 m. How much useful work did you do?

If you exhausted 500 J worth of thermal energy while doing the useful work above, how much did your internal energy change?

Body Efficiency

The efficiency of the human body in converting chemical potential energy into useful work is known as the mechanical efficiency of the body. We often calculate the body’s mechanical efficiency, as a percentage:

(2)

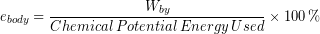
Thermal energy generated during the chemical reactions that power muscle contractions along with friction in joints and other tissues reduce the efficiency of humans to about 25 %.^[1]

“Alas, our bodies are not 100 % efficient at converting food energy into mechanical output. But at about 25 % efficiency, we’re surprisingly good considering that most cars are around 20 %, and that an Iowa cornfield is only about 1.5 % efficient at converting incoming sunlight into chemical [potential energy] storage.” ^[2]For an excellent discussion of human mechanical efficiency and comparisons with other machines and fuel sources, see MPG of a Human by Tom Murphy, the source of the previous quote.

Everyday Example: Energy to Climb Stairs

Assuming a 20% mechanical efficiency in climbing stairs, how much does your internal energy decrease when a 65 kg person climbs a 15 m high flight of stairs? How much thermal energy does the person transfer to the environment as exhaust heat?

First, lets calculate the change in gravitational potential energy:

The person did work in converting chemical potential energy in their body to mechanical energy, specifically gravitational potential energy. However, they are only 20% efficient, which means that only 1/5 of the chemical potential energy they use goes into doing useful work. Therefore the change in chemical potential energy must have been 5x greater than the mechanical work output

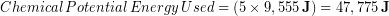
The chemical potential energy used came out of the person’s internal energy so:

We can use the First Law of Thermodynamics to find the thermal energy exhausted by the person:

(3)

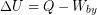
Rearranging for :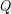

We find that the heat is negative, which makes sense because the person exhausts thermal energy out of the body and into to the environment while climbing the stairs.

Alternatively, we could have known right off that the exhaust heat must be 4/5 of the total loss of internal energy, because only 1/5 went into doing useful work. So the exhaust heat should be:

Food Calories

For historical reasons we often measure thermal energy and heat in units of calories (cal) instead of Joules. There are 4.184 Joules per calorie. We measure chemical potential energy stored in food with units of 1000 calories, or kilocalories (kcal) and we sometimes write kilocalories as Calories (Cal) with with capital C instead of a lowercase c. For example, a bagel with 350 Cal has 350 kcal, or 350,000 cal. Converting to Joules, that would be in the bagel.

Everyday Examples

What fraction of a bagel would you need to eat in order to make up for the 47,775 J loss of internal energy (as chemical potential energy) that we calculated in the previous everyday example about climbing stairs?

There are 1,464,400 J/bagel

Therefore we need to eat:

Reinforcement Exercises

How many Joules of energy are stored in a 260 Calorie candy bar?

How many candy bars would you need to eat to make up for the loss of internal energy we found in the previous everyday example?

Conservation of Mass and of Energy

We often talk about “burning” calories in order to lose weight, but what does that really mean scientifically?. First, we really we mean lose mass that is the measure of how much stuff is in our bodies and weight depends on where you are (it’s different on the moon). Second, our bodies can’t just interchange mass and energy — they aren’t the same physical quantity and don’t even have the same units. So how do we actually lose mass by exercising? We don’t actually shed the atoms and molecules that make up body tissues like fat by “burning” them. Instead, we break down the fat molecules into smaller molecules and then break bonds within those molecules to release chemical potential energy, which we eventually convert to work and exhaust heat. The atoms and smaller molecules that resulting from breaking the bonds combine to form carbon dioxide and water vapor (CO₂ and H₂O) and we breath them out. We also excrete a bit as H₂O in sweat and urine. The process is similar to burning wood in campfire — in the end you have much less mass of ash than you did original wood. Where did the rest of the mass go? Into the air as CO₂ and H₂O. The same is true for the fuel burned by your car. For more on this concept see the video below.

A YouTube element has been excluded from this version of the text. You can view it online here: https://openoregon.pressbooks.pub/bodyphysics/?p=1067

The really amazing fact is that your body completes this chemical process without the excessive temperatures associated with burning wood or fuel, which would damage your tissues. The body’s trick is to use enzymes, which are highly specialized molecules that act as catalysts to improve the speed and efficiency of chemical reactions, as described and animated in the beginning of the following video:

A YouTube element has been excluded from this version of the text. You can view it online here: https://openoregon.pressbooks.pub/bodyphysics/?p=1067

General Efficiency

Similar to the body efficiency, the efficiency of any energetic process can be described as the amount of energy converted from the input form to the desired form divided by the original input amount. The following chart outlines the efficiencies of various systems at converting energy various forms. The chart does not account for the cost, hazard risk, or environmental impact associated with the required fuel, construction, maintenance, and by-products of each system.

The Efficiency of the Human Body Compared to Other Systems

System	Input Energy Form	Desired Output Form	Max Efficiency
Human Body	Chemical Potential	Mechanical	25 %
Automobile Engine	Chemical Potential	Mechanical	25 %
Coal/Oil/Gas Fired Stream Turbine Power Plants	Chemical Potential	Electrical	47%
Combined Cycle Gas Power Plants	Chemical Potential	Electrical	58 %
Biomass/Biogas	Kinetic	Electrical	40%
Nuclear	Kinetic	Electrical	36%
Solar-Photovoltaic Power Plant	Sunlight (Electromagnetic)	Electrical	15%
Solar-Thermal Power Plant	Sunlight (Electromagnetic)	Electrical	23%
Hydroelectric and Tidal Power Plants	Gravitational Potential	Electrical	90%+

^{[3] [4] [5]}

Check out the energy systems tab in this simulation to visualize different energy conversion systems

---

1. "The maximum work and mechanical efficiency of human muscles, and their most economical speed" by A. V. Hill,National Library of Medicine, U.S. National institutes of Health↵
   
2. "MPG of a Human" by Tom Murphy, Do The Math, UCSD Physics Department↵
   
3. "Managing Water in the West: Hydroelectric Power" by Bureau of Reclimation, U.S. Department of the Interior↵
   
4. "Efficiency in Electricity Generation" by EURELECTRIC “Preservation of Resources” Working Group’s “Upstream” Sub-Group in collaboration with VGB, Union of the Electricity Industry↵
   
5. "Efficiency of Energy Conversion Devices" by John E. Dutton e-Education Institute, Penn State College of Earth and Mineral Sciences↵