8.4: Physical Model for Terminal Velocity
( \newcommand{\kernel}{\mathrm{null}\,}\)
After jumping, a skydiver begins gaining speed which increases the air resistance they experience. Eventually they will move fast enough that the air resistance is equal in size to their weight, but in opposite direction so they have no net force. This processes is illustrated by free body diagrams for a skydiver with 90 kg mass in the following image:

Free body diagrams of a person with 90 kg mass during a skydive. The initial speed is zero, so drag force is zero. As speed increases, the drag force grows, eventually cancelling out the person’s weight. At that point acceleration is zero and terminal velocity is reached.
Dynamic Equilibrium
With a net force of zero the skydiver must be in equilibrium, but they are not in static equilibrium because they are not static (motionless). Instead they are in dynamic equilibrium, which means that they are moving, but the motion isn’t changing because all the forces are still balanced (net force is zero). This concept is summarized by Newton's First Law, which tells us that an object’s motion will not change unless it experiences a net force. Newton’s first law is sometimes called the Law of Inertia because inertia is the name given to an object’s tendency to resist changes in motion. Newton's First Law applies to objects that are not moving and to objects that are already moving. Regarding the skydiver, we are applying Newton’s First Law to translational motion (back and forth, up and down), but it also holds for the effect of net torques on changes in rotational motion. Changes in motion are known as accelerations and we will learn more about how net forces cause translational accelerations in upcoming chapters.
Reinforcement Exercises
Using above the statement of Newton’s first law as it applies to net forces and translational motion as an example, write out Newton’s 1st Law as it applies to torques and changes in rotational motion
Dependence of Terminal Velocity on Mass
We already know from our experimental work during the Unit 3 lab that increasing mass leads to increasing terminal speed. We can now understand that this behavior occurs because greater mass leads to a greater weight and thus a greater speed is reached before the drag force (air resistance) is large enough to balance out the weight.
Everyday Examples
First-time skydivers are typically attached to an instructor (tandem skydiving). During a tandem skydive the bodies are stacked, so the shape and cross-sectional area of the object don’t change much, but the mass does. As a consequence, the terminal speed for tandem diving would be high enough to noticeably reduce the fall time and possibly be dangerous. Increasing the air resistance to account for the extra mass is accomplished by deploying a small drag chute that trails behind the skydivers, as seen in the photo below.

Tandem skydivers with a small speed-limiting drag chute trailing behind. Image Credit: Fallschirm Tandemsprung bei Jochen Schweizer By Jochen Schweizer via Wikimedia Commons
A Physical Model for Terminal Velocity
When the skydiver has reached terminal speed and remains in a state of dynamic equilibrium, we know the size of the drag force must be equal to the skydiver’s weight, but in the opposite direction. This concept will allow us to determine how the skydiver’s mass should affect terminal speed. We start be equating the air resistance with the weight:
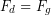
Then we insert the formulas for air resistance and for weight of an object near Earth’s surface. We designate the speed in the resulting equation 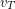 because these two forces are only equal at terminal speed.
because these two forces are only equal at terminal speed.
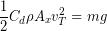
We then need to solve the above equation for the terminal speed.
(1)
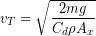
Everyday Examples
Let’s estimate the terminal speed of the human body. We start with the previous equation:
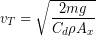
 . Drag coefficient and cross sectional area depend on body orientation, so let’s assume a standard skydiving posture: flat, horizontal, with arms and legs spread. In this case the drag coefficient will likely be 0.4-1.3. A reasonable value would be
. Drag coefficient and cross sectional area depend on body orientation, so let’s assume a standard skydiving posture: flat, horizontal, with arms and legs spread. In this case the drag coefficient will likely be 0.4-1.3. A reasonable value would be  [2]. To approximate the cross-sectional area we can use the authors average width of 0.3 m and height of 1.5 m for an area of
[2]. To approximate the cross-sectional area we can use the authors average width of 0.3 m and height of 1.5 m for an area of 
![]()
Reinforcement Exercises
You already have data on how the terminal speed depends on mass. We acquired this data using coffee filters in the Unit 3 Lab. Looking back at that data, does that data support our physical model for terminal speed? [Hint: If our empirical model (fit equation) suggests that terminal speed depends on mass in the same way as the physical model then yes, our data supports our physical model. Our physical model says that the terminal speed depends on the square root of the mass. Does your empirical fit equation support that result?]
Acceleration During a Skydive
We have now analyzed the skydive after terminal speed was reached. Prior to this point the forces of drag and weight are not equal, therefore the skydiver is not in dynamic equilibrium and speed will change over time. In order to analyze the early part of the skydive, or the motion of any object that is not in equilibrium, we need to learn how to quantify changes in speed and/or direction.
- By Jochen Schweizer GmbH [CC BY-SA 4.0 (https://creativecommons.org/licenses/by-sa/4.0)], from Wikimedia Commons↵
- "Drag Coefficient" by Engineering Toolbox↵


