2.6: Problems
( \newcommand{\kernel}{\mathrm{null}\,}\)
1. Thermometers normally use either mercury or alcohol as their working fluid. If the level of the fluid rises or falls, does this violate conservation of mass?
2. The ratios of the masses of different types of atoms were determined a century before anyone knew any actual atomic masses in units of kg. One finds, for example, that when ordinary table salt, NaCl, is melted, the chlorine atoms bubble off as a gas, leaving liquid sodium metal. Suppose the chlorine escapes, so that its mass cannot be directly determined by weighing. Experiments show that when 1.00000 kg of NaCl is treated in this way, the mass of the remaining sodium metal is 0.39337 kg. Based on this information, determine the ratio of the mass of a chlorine atom to that of a sodium atom (answer check available at lightandmatter.com)
3. An atom of the most common naturally occurring uranium isotope breaks up spontaneously into a thorium atom plus a helium atom. The masses are as follows:
| uranium | 3.95292849 X 1025 kg |
| thorium | 3.88638748 X 1025 kg |
| helium | 6.646481 X 1027 kg |
Each of these experimentally determined masses is uncertain in its last decimal place. Is mass conserved in this process to within the accuracy of the experimental data? How would you interpret this?
4. If two spherical water droplets of radius b combine to make a single droplet, what is its radius? (Assume that water has constant density.)
5. Make up an experiment that would test whether mass is conserved in an animal's metabolic processes.
6. The figure shows a hydraulic jack. What is the relationship between the distance traveled by the plunger and the distance traveled by the object being lifted, in terms of the cross-sectional areas?

7. In an example in this chapter, I argued that a stream of water must change its cross-sectional area as it rises or falls. Suppose that the stream of water is confined to a constant-diameter pipe. Which assumption breaks down in this situation?
8. A river with a certain width and depth splits into two parts, each of which has the same width and depth as the original river. What can you say about the speed of the current after the split?
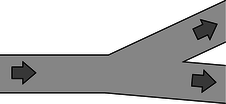
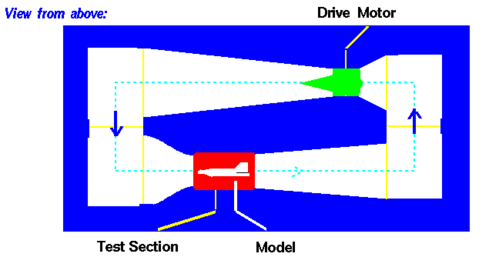
9. The diagram shows a cross-section of a wind tunnel of the kind used, for example, to test designs of airplanes. Under normal conditions of use, the density of the air remains nearly constant throughout the whole wind tunnel. How can the speed of the air be controlled and calculated? (Diagram by NASA, Glenn Research Center.)
10. A water wave is in a tank that extends horizontally from x=0 to x=a, and from z=0 to z=b. We assume for simplicity that at a certain moment in time the height y of the water's surface only depends on x, not z, so that we can effectively ignore the z coordinate. Under these assumptions, the total volume of the water in the tank is
V=ba∫0y(x)dx
Since the density of the water is essentially constant, conservation of mass requires that V is always the same. When the water is calm, we have y=h, where h=V/ab. If two different wave patterns move into each other, we might imagine that they would add in the sense that ytotal−h=(y1−h)+(y2−h). Show that this type of addition is consistent with conservation of mass.
11. The figure shows the position of a falling ball at equal time intervals, depicted in a certain frame of reference. On a similar grid, show how the ball's motion would appear in a frame of reference that was moving horizontally at a speed of one box per unit time relative to the first frame.
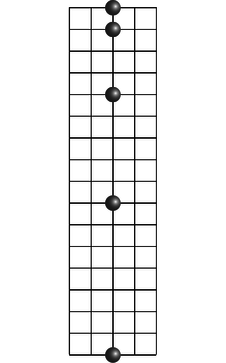
12. (solution in the pdf version of the book) The figure shows the motion of a point on the rim of a rolling wheel. (The shape is called a cycloid.) Suppose bug A is riding on the rim of the wheel on a bicycle that is rolling, while bug B is on the spinning wheel of a bike that is sitting upside down on the floor. Bug A is moving along a cycloid, while bug B is moving in a circle. Both wheels are doing the same number of revolutions per minute. Which bug has a harder time holding on, or do they find it equally difficult?

Contributors and Attributions
Benjamin Crowell (Fullerton College). Conceptual Physics is copyrighted with a CC-BY-SA license.


