14.4: The Atom
- Page ID
- 989
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)You can learn a lot by taking a car engine apart, but you will have learned a lot more if you can put it all back together again and make it run. Half the job of reductionism is to break nature down into its smallest parts and understand the rules those parts obey. The second half is to show how those parts go together, and that is our goal in this chapter. We have seen how certain features of all atoms can be explained on a generic basis in terms of the properties of bound states, but this kind of argument clearly cannot tell us any details of the behavior of an atom or explain why one atom acts differently from another.
The biggest embarrassment for reductionists is that the job of putting things back together job is usually much harder than the taking them apart. Seventy years after the fundamentals of atomic physics were solved, it is only beginning to be possible to calculate accurately the properties of atoms that have many electrons. Systems consisting of many atoms are even harder. Supercomputer manufacturers point to the folding of large protein molecules as a process whose calculation is just barely feasible with their fastest machines. The goal of this chapter is to give a gentle and visually oriented guide to some of the simpler results about atoms.
Classifying States
We'll focus our attention first on the simplest atom, hydrogen, with one proton and one electron. We know in advance a little of what we should expect for the structure of this atom. Since the electron is bound to the proton by electrical forces, it should display a set of discrete energy states, each corresponding to a certain standing wave pattern. We need to understand what states there are and what their properties are.
What properties should we use to classify the states? The most sensible approach is to used conserved quantities. Energy is one conserved quantity, and we already know to expect each state to have a specific energy. It turns out, however, that energy alone is not sufficient. Different standing wave patterns of the atom can have the same energy.
Momentum is also a conserved quantity, but it is not particularly appropriate for classifying the states of the electron in a hydrogen atom. The reason is that the force between the electron and the proton results in the continual exchange of momentum between them. (Why wasn't this a problem for energy as well? Kinetic energy and momentum are related by \(K=p^2/2m\), so the much more massive proton never has very much kinetic energy. We are making an approximation by assuming all the kinetic energy is in the electron, but it is quite a good approximation.)
Angular momentum does help with classification. There is no transfer of angular momentum between the proton and the electron, since the force between them is a center-to-center force, producing no torque.
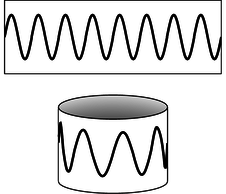
a / Eight wavelengths fit around this circle (\(\ell=8\)).
Like energy, angular momentum is quantized in quantum physics. As an example, consider a quantum wave-particle confined to a circle, like a wave in a circular moat surrounding a castle. A sine wave in such a “quantum moat” cannot have any old wavelength, because an integer number of wavelengths must fit around the circumference, \(C\), of the moat. The larger this integer is, the shorter the wavelength, and a shorter wavelength relates to greater momentum and angular momentum. Since this integer is related to angular momentum, we use the symbol \(\ell\) for it:
\[\begin{equation*} \lambda = C / \ell \end{equation*}\]
The angular momentum is
\[\begin{equation*} L = rp . \end{equation*}\]
Here, \(r=C/2\pi \), and \(p=h/\lambda=h\ell/C\), so
\[\begin{align*} L &= \frac{C}{2\pi}\cdot\frac{h\ell}{C} \\ &= \frac{h}{2\pi}\ell \end{align*}\]
In the example of the quantum moat, angular momentum is quantized in units of \(h/2\pi \). This makes \(h/2\pi \) a pretty important number, so we define the abbreviation \(\hbar=h/2\pi \). This symbol is read “h-bar.”
In fact, this is a completely general fact in quantum physics, not just a fact about the quantum moat:
Quantization of angular momentum
The angular momentum of a particle due to its motion through space is quantized in units of \(\hbar\).
What is the angular momentum of the wavefunction shown at the beginning of the section?
- Answer
-
(answer in the back of the PDF version of the book)
Three dimensions
Our discussion of quantum-mechanical angular momentum has so far been limited to rotation in a plane, for which we can simply use positive and negative signs to indicate clockwise and counterclockwise directions of rotation. A hydrogen atom, however, is unavoidably three-dimensional. The classical treatment of angular momentum in three-dimensions has been presented in section 4.3; in general, the angular momentum of a particle is defined as the vector cross product \(\mathbf{r}\times\mathbf{p}\).
There is a basic problem here: the angular momentum of the electron in a hydrogen atom depends on both its distance \(\mathbf{r}\) from the proton and its momentum \(\mathbf{p}\), so in order to know its angular momentum precisely it would seem we would need to know both its position and its momentum simultaneously with good accuracy. This, however, seems forbidden by the Heisenberg uncertainty principle.
Actually the uncertainty principle does place limits on what can be known about a particle's angular momentum vector, but it does not prevent us from knowing its magnitude as an exact integer multiple of \(\hbar\). The reason is that in three dimensions, there are really three separate uncertainty principles:
\[\begin{align*} \Delta p_x \Delta x &\gtrsim h \\ \Delta p_y \Delta y &\gtrsim h \\ \Delta p_z \Delta z &\gtrsim h \end{align*}\]
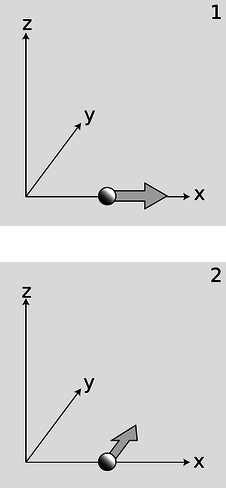
b / Reconciling the uncertainty principle with the definition of angular momentum.
Now consider a particle, b/1, that is moving along the \(x\) axis at position \(x\) and with momentum \(p_x\). We may not be able to know both \(x\) and \(p_x\) with unlimited accurately, but we can still know the particle's angular momentum about the origin exactly: it is zero, because the particle is moving directly away from the origin.
Suppose, on the other hand, a particle finds itself, b/2, at a position \(x\) along the \(x\) axis, and it is moving parallel to the \(y\) axis with momentum \(p_y\). It has angular momentum \(xp_y\) about the \(z\) axis, and again we can know its angular momentum with unlimited accuracy, because the uncertainty principle only relates \(x\) to \(p_x\) and \(y\) to \(p_y\). It does not relate \(x\) to \(p_y\).
As shown by these examples, the uncertainty principle does not restrict the accuracy of our knowledge of angular momenta as severely as might be imagined. However, it does prevent us from knowing all three components of an angular momentum vector simultaneously. The most general statement about this is the following theorem, which we present without proof:
The angular momentum vector in quantum physics
The most that can be known about an angular momentum vector is its magnitude and one of its three vector components. Both are quantized in units of \(\hbar\).

c / A cross-section of a hydrogen wavefunction.
The hydrogen atom
Deriving the wavefunctions of the states of the hydrogen atom from first principles would be mathematically too complex for this book, but it's not hard to understand the logic behind such a wavefunction in visual terms. Consider the wavefunction from the beginning of the section, which is reproduced in figure c. Although the graph looks three-dimensional, it is really only a representation of the part of the wavefunction lying within a two-dimensional plane. The third (up-down) dimension of the plot represents the value of the wavefunction at a given point, not the third dimension of space. The plane chosen for the graph is the one perpendicular to the angular momentum vector.
Each ring of peaks and valleys has eight wavelengths going around in a circle, so this state has \(L=8\hbar\), i.e., we label it \(\ell=8\). The wavelength is shorter near the center, and this makes sense because when the electron is close to the nucleus it has a lower electrical energy, a higher kinetic energy, and a higher momentum.
Between each ring of peaks in this wavefunction is a nodal circle, i.e., a circle on which the wavefunction is zero. The full three-dimensional wavefunction has nodal spheres: a series of nested spherical surfaces on which it is zero. The number of radii at which nodes occur, including \(r=\infty\), is called \(n\), and \(n\) turns out to be closely related to energy. The ground state has \(n=1\) (a single node only at \(r=\infty\)), and higher-energy states have higher \(n\) values. There is a simple equation relating \(n\) to energy, which we will discuss in subsection 13.4.4.
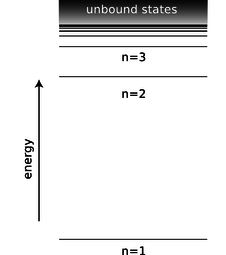
d / The energy of a state in the hydrogen atom depends only on its \(n\) quantum number.
The numbers \(n\) and \(\ell\), which identify the state, are called its quantum numbers. A state of a given \(n\) and \(\ell\) can be oriented in a variety of directions in space. We might try to indicate the orientation using the three quantum numbers \(\ell_x=L_x/\hbar\), \(\ell_y=L_y/\hbar\), and \(\ell_z=L_z/\hbar\). But we have already seen that it is impossible to know all three of these simultaneously. To give the most complete possible description of a state, we choose an arbitrary axis, say the \(z\) axis, and label the state according to \(n\), \(\ell\), and \(\ell_z\).6
Angular momentum requires motion, and motion implies kinetic energy. Thus it is not possible to have a given amount of angular momentum without having a certain amount of kinetic energy as well. Since energy relates to the \(n\) quantum number, this means that for a given \(n\) value there will be a maximum possible . It turns out that this maximum value of equals \(n-1\).
In general, we can list the possible combinations of quantum numbers as follows:
| n can equal 1, 2, 3, … |
| l can range from 0 ton − 1, in steps of 1 |
| lz can range fromell toell, in steps of 1 |
Applying these rules, we have the following list of states:
| n = 1, | l=0, | lz=0 | one state |
| n = 2, | l=0, | lz=0 | one state |
| n = 2, | l=1, | lz=-1, 0, or 1 | three states |
self-check:
Continue the list for \(n=3\).
(answer in the back of the PDF version of the book)
Figure e on page 882 shows the lowest-energy states of the hydrogen atom. The left-hand column of graphs displays the wavefunctions in the \(x-y\) plane, and the right-hand column shows the probability distribution in a three-dimensional representation.
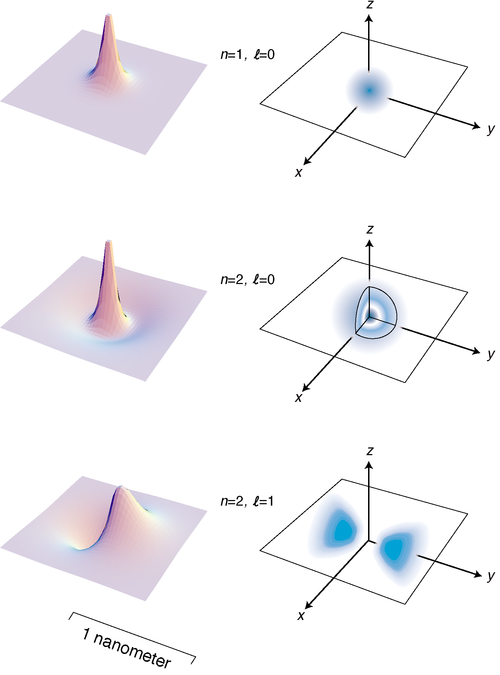
e / The three states of the hydrogen atom having the lowest energies.
Discussion Questions
◊ The quantum number \(n\) is defined as the number of radii at which the wavefunction is zero, including \(r=\infty\). Relate this to the features of the figures on the facing page.
◊ Based on the definition of \(n\), why can't there be any such thing as an \(n=0\) state?
◊ Relate the features of the wavefunction plots in figure e to the corresponding features of the probability distribution pictures.
◊ How can you tell from the wavefunction plots in figure e which ones have which angular momenta?
◊ Criticize the following incorrect statement: “The \(\ell=8\) wavefunction in figure c has a shorter wavelength in the center because in the center the electron is in a higher energy level.”
◊ Discuss the implications of the fact that the probability cloud in of the \(n=2\), \(\ell=1\) state is split into two parts.
Energies of states in hydrogen
History
The experimental technique for measuring the energy levels of an atom accurately is spectroscopy: the study of the spectrum of light emitted (or absorbed) by the atom. Only photons with certain energies can be emitted or absorbed by a hydrogen atom, for example, since the amount of energy gained or lost by the atom must equal the difference in energy between the atom's initial and final states. Spectroscopy had become a highly developed art several decades before Einstein even proposed the photon, and the Swiss spectroscopist Johann Balmer determined in 1885 that there was a simple equation that gave all the wavelengths emitted by hydrogen. In modern terms, we think of the photon wavelengths merely as indirect evidence about the underlying energy levels of the atom, and we rework Balmer's result into an equation for these atomic energy levels:
\[\begin{equation*} E_n = -\frac{2.2\times10^{-18}\ \text{J}}{n^2} , \end{equation*}\]
This energy includes both the kinetic energy of the electron and the electrical energy. The zero-level of the electrical energy scale is chosen to be the energy of an electron and a proton that are infinitely far apart. With this choice, negative energies correspond to bound states and positive energies to unbound ones.
Where does the mysterious numerical factor of \(2.2\times10^{-18}\ \text{J}\) come from? In 1913 the Danish theorist Niels Bohr realized that it was exactly numerically equal to a certain combination of fundamental physical constants:
\[\begin{equation*} E_n = -\frac{mk^2e^4}{2\hbar^2}\cdot\frac{1}{n^2} , \end{equation*}\]
where \(m\) is the mass of the electron, and \(k\) is the Coulomb force constant for electric forces.
Bohr was able to cook up a derivation of this equation based on the incomplete version of quantum physics that had been developed by that time, but his derivation is today mainly of historical interest. It assumes that the electron follows a circular path, whereas the whole concept of a path for a particle is considered meaningless in our more complete modern version of quantum physics. Although Bohr was able to produce the right equation for the energy levels, his model also gave various wrong results, such as predicting that the atom would be flat, and that the ground state would have \(\ell=1\) rather than the correct \(\ell=0\).
Approximate treatment
Rather than leaping straight into a full mathematical treatment, we'll start by looking for some physical insight, which will lead to an approximate argument that correctly reproduces the form of the Bohr equation.
A typical standing-wave pattern for the electron consists of a central oscillating area surrounded by a region in which the wavefunction tails off. As discussed in subsection 13.3.6, the oscillating type of pattern is typically encountered in the classically allowed region, while the tailing off occurs in the classically forbidden region where the electron has insufficient kinetic energy to penetrate according to classical physics. We use the symbol \(r\) for the radius of the spherical boundary between the classically allowed and classically forbidden regions. Classically, \(r\) would be the distance from the proton at which the electron would have to stop, turn around, and head back in.
If \(r\) had the same value for every standing-wave pattern, then we'd essentially be solving the particle-in-a-box problem in three dimensions, with the box being a spherical cavity. Consider the energy levels of the particle in a box compared to those of the hydrogen atom, f.
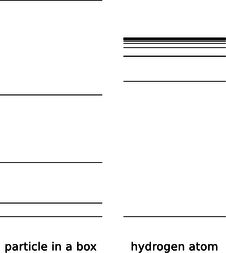
f / The energy levels of a particle in a box, contrasted with those of the hydrogen atom.
They're qualitatively different. The energy levels of the particle in a box get farther and farther apart as we go higher in energy, and this feature doesn't even depend on the details of whether the box is two-dimensional or three-dimensional, or its exact shape. The reason for the spreading is that the box is taken to be completely impenetrable, so its size, \(r\), is fixed. A wave pattern with \(n\) humps has a wavelength proportional to \(r/n\), and therefore a momentum proportional to \(n\), and an energy proportional to \(n^2\). In the hydrogen atom, however, the force keeping the electron bound isn't an infinite force encountered when it bounces off of a wall, it's the attractive electrical force from the nucleus. If we put more energy into the electron, it's like throwing a ball upward with a higher energy --- it will get farther out before coming back down. This means that in the hydrogen atom, we expect \(r\) to increase as we go to states of higher energy. This tends to keep the wavelengths of the high energy states from getting too short, reducing their kinetic energy. The closer and closer crowding of the energy levels in hydrogen also makes sense because we know that there is a certain energy that would be enough to make the electron escape completely, and therefore the sequence of bound states cannot extend above that energy.
When the electron is at the maximum classically allowed distance \(r\) from the proton, it has zero kinetic energy. Thus when the electron is at distance \(r\), its energy is purely electrical:
\[\begin{equation*} E = -\frac{ke^2}{r} \tag{1} \end{equation*}\]
Now comes the approximation. In reality, the electron's wavelength cannot be constant in the classically allowed region, but we pretend that it is. Since \(n\) is the number of nodes in the wavefunction, we can interpret it approximately as the number of wavelengths that fit across the diameter \(2r\). We are not even attempting a derivation that would produce all the correct numerical factors like 2 and \(\pi \) and so on, so we simply make the approximation
\[\begin{equation*} \lambda \sim \frac{r}{n} . \tag{2} \end{equation*}\]
Finally we assume that the typical kinetic energy of the electron is on the same order of magnitude as the absolute value of its total energy. (This is true to within a factor of two for a typical classical system like a planet in a circular orbit around the sun.) We then have
\[\begin{align*} \text{absolute}&\text{ value of total energy} \\ &= \frac{ke^2}{r} \notag \\ &\sim K \notag = p^2/2m \notag \\ &= (h/\lambda)^2/2m \notag \\ &\sim h^2n^2/2mr^2 \tag{3} \end{align*}\]
We now solve the equation \(ke^2/r \sim h^2n^2 / 2mr^2\) for \(r\) and throw away numerical factors we can't hope to have gotten right, yielding
\[\begin{equation*} r \sim \frac{h^2n^2}{mke^2} .\tag{4} \end{equation*}\]
Plugging \(n=1\) into this equation gives \(r=2\) nm, which is indeed on the right order of magnitude. Finally we combine equations (4) and (1) to find
\[\begin{equation*} E \sim -\frac{mk^2e^4}{h^2n^2} , \end{equation*}\]
which is correct except for the numerical factors we never aimed to find.
Exact treatment of the ground state
The general proof of the Bohr equation for all values of \(n\) is beyond the mathematical scope of this book, but it's fairly straightforward to verify it for a particular \(n\), especially given a lucky guess as to what functional form to try for the wavefunction. The form that works for the ground state is
\[\begin{equation*} \Psi = ue^{-r/a} , \end{equation*}\]
where \(r=\sqrt{x^2+y^2+z^2}\) is the electron's distance from the proton, and \(u\) provides for normalization. In the following, the result \(\partial r/\partial x=x/r\) comes in handy. Computing the partial derivatives that occur in the Laplacian, we obtain for the \(x\) term
\[\begin{align*} \frac{\partial\Psi}{\partial x} &= \frac{\partial \Psi}{\partial r} \frac{\partial r}{\partial x} \\ &= -\frac{x}{ar} \Psi \\ \frac{\partial^2\Psi}{\partial x^2} &= -\frac{1}{ar} \Psi -\frac{x}{a}\left(\frac{\partial}{dx}\frac{1}{r}\right)\Psi+ \left( \frac{x}{ar}\right)^2 \Psi\\ &= -\frac{1}{ar} \Psi +\frac{x^2}{ar^3}\Psi+ \left( \frac{x}{ar}\right)^2 \Psi , \text{so} \nabla^2\Psi &= \left( -\frac{2}{ar} + \frac{1}{a^2} \right) \Psi . \end{align*}\]
The Schrödinger equation gives
\[\begin{align*} E\cdot\Psi &= -\frac{\hbar^2}{2m}\nabla^2\Psi + U\cdot\Psi \\ &= \frac{\hbar^2}{2m}\left( \frac{2}{ar} - \frac{1}{a^2} \right)\Psi -\frac{ke^2}{r}\cdot\Psi \end{align*}\]
If we require this equation to hold for all \(r\), then we must have equality for both the terms of the form \((\text{constant})\times\Psi\) and for those of the form \((\text{constant}/r)\times\Psi\). That means
\[\begin{align*} E &= -\frac{\hbar^2}{2ma^2} \\ \text{and} \\ 0 &= \frac{\hbar^2}{mar} -\frac{ke^2}{r} . \end{align*}\]
These two equations can be solved for the unknowns \(a\) and \(E\), giving
\[\begin{align*} a &= \frac{\hbar^2}{mke^2} \\ \text{and}\\ E &= -\frac{mk^2e^4}{2\hbar^2} , \end{align*}\]
where the result for the energy agrees with the Bohr equation for \(n=1\). The calculation of the normalization constant \(u\) is relegated to homework problem 36.
We've verified that the function \(\Psi = he^{-r/a}\) is a solution to the Schrödinger equation, and yet it has a kink in it at \(r=0\). What's going on here? Didn't I argue before that kinks are unphysical?
- Answer
-
(answer in the back of the PDF version of the book)
In example 16 on page 861, I argued that the existence of the \(\text{H}_2\) molecule could essentially be explained by a particle-in-a-box argument: the molecule is a bigger box than an individual atom, so each electron's wavelength can be longer, its kinetic energy lower. Now that we're in possession of a mathematical expression for the wavefunction of the hydrogen atom in its ground state, we can make this argument a little more rigorous and detailed. Suppose that two hydrogen atoms are in a relatively cool sample of monoatomic hydrogen gas. Because the gas is cool, we can assume that the atoms are in their ground states. Now suppose that the two atoms approach one another. Making use again of the assumption that the gas is cool, it is reasonable to imagine that the atoms approach one another slowly. Now the atoms come a little closer, but still far enough apart that the region between them is classically forbidden. Each electron can tunnel through this classically forbidden region, but the tunneling probability is small. Each one is now found with, say, 99% probability in its original home, but with 1% probability in the other nucleus. Each electron is now in a state consisting of a superposition of the ground state of its own atom with the ground state of the other atom. There are two peaks in the superposed wavefunction, but one is a much bigger peak than the other.
An interesting question now arises. What are the relative phases of the two electrons? As discussed on page 855, the absolute phase of an electron's wavefunction is not really a meaningful concept. Suppose atom A contains electron Alice, and B electron Bob. Just before the collision, Alice may have wondered, “Is my phase positive right now, or is it negative? But of course I shouldn't ask myself such silly questions,” she adds sheepishly.

g / Example 23.
But relative phases are well defined. As the two atoms draw closer and closer together, the tunneling probability rises, and eventually gets so high that each electron is spending essentially 50% of its time in each atom. It's now reasonable to imagine that either one of two possibilities could obtain. Alice's wavefunction could either look like g/1, with the two peaks in phase with one another, or it could look like g/2, with opposite phases. Because relative phases of wavefunctions are well defined, states 1 and 2 are physically distinguishable. In particular, the kinetic energy of state 2 is much higher; roughly speaking, it is like the two-hump wave pattern of the particle in a box, as opposed to 1, which looks roughly like the one-hump pattern with a much longer wavelength. Not only that, but an electron in state 1 has a large probability of being found in the central region, where it has a large negative electrical energy due to its interaction with both protons. State 2, on the other hand, has a low probability of existing in that region. Thus state 1 represents the true ground-state wavefunction of the \(\text{H}_2\) molecule, and putting both Alice and Bob in that state results in a lower energy than their total energy when separated, so the molecule is bound, and will not fly apart spontaneously.
State g/3, on the other hand, is not physically distinguishable from g/2, nor is g/4 from g/1. Alice may say to Bob, “Isn't it wonderful that we're in state 1 or 4? I love being stable like this.” But she knows it's not meaningful to ask herself at a given moment which state she's in, 1 or 4.
Solution
Add text here.
Discussion Questions
- States of hydrogen with \(n\) greater than about 10 are never observed in the sun. Why might this be?
- Sketch graphs of \(r\) and \(E\) versus \(n\) for the hydrogen, and compare with analogous graphs for the one-dimensional particle in a box.
Electron spin
It's disconcerting to the novice ping-pong player to encounter for the first time a more skilled player who can put spin on the ball. Even though you can't see that the ball is spinning, you can tell something is going on by the way it interacts with other objects in its environment. In the same way, we can tell from the way electrons interact with other things that they have an intrinsic spin of their own. Experiments show that even when an electron is not moving through space, it still has angular momentum amounting to \(\hbar/2\).
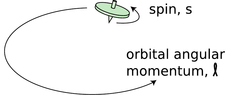
h / The top has angular momentum both because of the motion of its center of mass through space and due to its internal rotation. Electron spin is roughly analogous to the intrinsic spin of the top.
This may seem paradoxical because the quantum moat, for instance, gave only angular momenta that were integer multiples of \(\hbar\), not half-units, and I claimed that angular momentum was always quantized in units of \(\hbar\), not just in the case of the quantum moat. That whole discussion, however, assumed that the angular momentum would come from the motion of a particle through space. The \(\hbar/2\) angular momentum of the electron is simply a property of the particle, like its charge or its mass. It has nothing to do with whether the electron is moving or not, and it does not come from any internal motion within the electron. Nobody has ever succeeded in finding any internal structure inside the electron, and even if there was internal structure, it would be mathematically impossible for it to result in a half-unit of angular momentum.
We simply have to accept this \(\hbar/2\) angular momentum, called the “spin” of the electron --- Mother Nature rubs our noses in it as an observed fact.
Protons and neutrons have the same \(\hbar/2\) spin, while photons have an intrinsic spin of \(\hbar\). In general, half-integer spins are typical of material particles. Integral values are found for the particles that carry forces: photons, which embody the electric and magnetic fields of force, as well as the more exotic messengers of the nuclear and gravitational forces.
As was the case with ordinary angular momentum, we can describe spin angular momentum in terms of its magnitude, and its component along a given axis. We write \(s\) and \(s_z\) for these quantities, expressed in units of \(\hbar\), so an electron has \(s=1/2\) and \(s_z=+1/2\) or \(-1/2\).
Taking electron spin into account, we need a total of four quantum numbers to label a state of an electron in the hydrogen atom: \(n\), \(\ell\), \(\ell_z\), and \(s_z\). (We omit \(s\) because it always has the same value.) The symbols and include only the angular momentum the electron has because it is moving through space, not its spin angular momentum. The availability of two possible spin states of the electron leads to a doubling of the numbers of states:
| n = 1, | l=0, | lz=0, | sz = + 1 / 2 or − 1 / 2 | two states |
| n = 2, | l=0, | lz=0, | sz = + 1 / 2 or − 1 / 2 | two states |
| n = 2, | l=1, | lz=-1, 0, or 1 | sz = + 1 / 2 or − 1 / 2 | six states |
A note about notation
There are unfortunately two inconsistent systems of notation for the quantum numbers we've been discussing. The notation I've been using is the one that is used in nuclear physics, but there is a different one that is used in atomic physics.
| nuclear physics | atomic physics |
| n | same |
| l | same |
| lx | no notation |
| ly | no notation |
| lz | m |
| s = 1 / 2 | no notation (sometimesσ) |
| sx | no notation |
| sy | no notation |
| sz | s |
he nuclear physics notation is more logical (not giving special status to the \(z\) axis) and more memorable (\(\ell_z\) rather than the obscure \(m\)), which is why I use it consistently in this book, even though nearly all the applications we'll consider are atomic ones.
We are further encumbered with the following historically derived letter labels, which deserve to be eliminated in favor of the simpler numerical ones:
| l=0 | l=1 | l=2 | l=3 |
| s | p | d | f |
| n = 1 | n = 2 | n = 3 | n = 4 | n = 5 | n = 6 | n = 7 |
| K | L | M | N | O | P | Q |
The spdf labels are used in both nuclear7 and atomic physics, while the KLMNOPQ letters are used only to refer to states of electrons.
And finally, there is a piece of notation that is good and useful, but which I simply haven't mentioned yet. The vector \(\mathbf{j}=\v c{\ell}+\mathbf{s}\) stands for the total angular momentum of a particle in units of \(\hbar\), including both orbital and spin parts. This quantum number turns out to be very useful in nuclear physics, because nuclear forces tend to exchange orbital and spin angular momentum, so a given energy level often contains a mixture of \(\ell\) and \(s\) values, while remaining fairly pure in terms of \(j\).
13.4.6 Atoms with more than one electron
What about other atoms besides hydrogen? It would seem that things would get much more complex with the addition of a second electron. A hydrogen atom only has one particle that moves around much, since the nucleus is so heavy and nearly immobile. Helium, with two, would be a mess. Instead of a wavefunction whose square tells us the probability of finding a single electron at any given location in space, a helium atom would need to have a wavefunction whose square would tell us the probability of finding two electrons at any given combination of points. Ouch! In addition, we would have the extra complication of the electrical interaction between the two electrons, rather than being able to imagine everything in terms of an electron moving in a static field of force created by the nucleus alone.
Despite all this, it turns out that we can get a surprisingly good description of many-electron atoms simply by assuming the electrons can occupy the same standing-wave patterns that exist in a hydrogen atom. The ground state of helium, for example, would have both electrons in states that are very similar to the \(n=1\) states of hydrogen. The second-lowest-energy state of helium would have one electron in an \(n=1\) state, and the other in an \(n=2\) states. The relatively complex spectra of elements heavier than hydrogen can be understood as arising from the great number of possible combinations of states for the electrons.
A surprising thing happens, however, with lithium, the three-electron atom. We would expect the ground state of this atom to be one in which all three electrons settle down into \(n=1\) states. What really happens is that two electrons go into \(n=1\) states, but the third stays up in an \(n=2\) state. This is a consequence of a new principle of physics:
The Pauli Exclusion Principle
Only one electron can ever occupy a given state.
There are two \(n=1\) states, one with \(s_z=+1/2\) and one with \(s_z=-1/2\), but there is no third \(n=1\) state for lithium's third electron to occupy, so it is forced to go into an \(n=2\) state.
It can be proved mathematically that the Pauli exclusion principle applies to any type of particle that has half-integer spin. Thus two neutrons can never occupy the same state, and likewise for two protons. Photons, however, are immune to the exclusion principle because their spin is an integer.
Deriving the periodic table
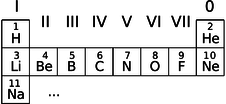
i / The beginning of the periodic table.
We can now account for the structure of the periodic table, which seemed so mysterious even to its inventor Mendeleev. The first row consists of atoms with electrons only in the \(n=1\) states:
| H |
1 electron in an n = 1 state |
| He |
2 electrons in the two n = 1 states |
The next row is built by filling the \(n=2\) energy levels:
| Li |
2 electrons in n = 1 states, 1 electron in an n = 2 state |
| Be |
2 electrons in n = 1 states, 2 electrons inn = 2 states |
| … | |
| O |
2 electrons in n = 1 states, 6 electrons in n = 2 states |
| F |
2 electrons in n = 1 states, 7 electrons in n = 2 states |
| Ne |
2 electrons in n = 1 states, 8 electrons in n = 2 states |
In the third row we start in on the \(n=3\) levels:
| Na |
2 electrons in n = 1 states, 8 electrons in n = 2 states, 1 electron in an n = 3 state |
We can now see a logical link between the filling of the energy levels and the structure of the periodic table. Column 0, for example, consists of atoms with the right number of electrons to fill all the available states up to a certain value of \(n\). Column I contains atoms like lithium that have just one electron more than that.
This shows that the columns relate to the filling of energy levels, but why does that have anything to do with chemistry? Why, for example, are the elements in columns I and VII dangerously reactive?

j / Hydrogen is highly reactive.
Consider, for example, the element sodium (Na), which is so reactive that it may burst into flames when exposed to air. The electron in the \(n=3\) state has an unusually high energy. If we let a sodium atom come in contact with an oxygen atom, energy can be released by transferring the \(n=3\) electron from the sodium to one of the vacant lower-energy \(n=2\) states in the oxygen. This energy is transformed into heat. Any atom in column I is highly reactive for the same reason: it can release energy by giving away the electron that has an unusually high energy.
Column VII is spectacularly reactive for the opposite reason: these atoms have a single vacancy in a low-energy state, so energy is released when these atoms steal an electron from another atom.
It might seem as though these arguments would only explain reactions of atoms that are in different rows of the periodic table, because only in these reactions can a transferred electron move from a higher-\(n\) state to a lower-\(n\) state. This is incorrect. An \(n=2\) electron in fluorine (F), for example, would have a different energy than an \(n=2\) electron in lithium (Li), due to the different number of protons and electrons with which it is interacting. Roughly speaking, the \(n=2\) electron in fluorine is more tightly bound (lower in energy) because of the larger number of protons attracting it. The effect of the increased number of attracting protons is only partly counteracted by the increase in the number of repelling electrons, because the forces exerted on an electron by the other electrons are in many different directions and cancel out partially.
Benjamin Crowell (Fullerton College). Conceptual Physics is copyrighted with a CC-BY-SA license.


