14.6: Problems

1. If a radioactive substance has a half-life of one year, does this mean that it will be completely decayed after two years? Explain.

2. What is the probability of rolling a pair of dice and getting “snake eyes,” i.e., both dice come up with ones?

3. Problem 3 has been deleted.

4. Problem 4 has been deleted.

5. Refer to the probability distribution for people's heights in figure f on page 828.
(a) Show that the graph is properly normalized.
(b) Estimate the fraction of the population having heights between 140 and 150 cm.(answer check available at lightandmatter.com)

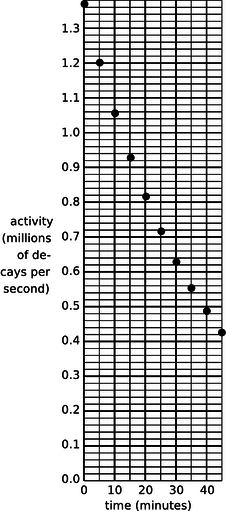
a / Problem 6.

6. (a) A nuclear physicist is studying a nuclear reaction caused in an accelerator experiment, with a beam of ions from the accelerator striking a thin metal foil and causing nuclear reactions when a nucleus from one of the beam ions happens to hit one of the nuclei in the target. After the experiment has been running for a few hours, a few billion radioactive atoms have been produced, embedded in the target. She does not know what nuclei are being produced, but she suspects they are an isotope of some heavy element such as Pb, Bi, Fr or U. Following one such experiment, she takes the target foil out of the accelerator, sticks it in front of a detector, measures the activity every 5 min, and makes a graph (figure). The isotopes she thinks may have been produced are:

isotope	half-life (minutes)
^211Pb	36.1
^214Pb	26.8
214Bi	19.7
^223Fr	21.8
^239U	23.5

Which one is it?
(b) Having decided that the original experimental conditions produced one specific isotope, she now tries using beams of ions traveling at several different speeds, which may cause different reactions. The following table gives the activity of the target 10, 20 and 30 minutes after the end of the experiment, for three different ion speeds.

	activity (millions of decays/s) after…
	10 min	20 min	30 min
first ion speed	1.933	0.832	0.382
second ion speed	1.200	0.545	0.248
third ion speed	7.211	1.296	0.248

Since such a large number of decays is being counted, assume that the data are only inaccurate due to rounding off when writing down the table. Which are consistent with the production of a single isotope, and which imply that more than one isotope was being created?

7. Devise a method for testing experimentally the hypothesis that a gambler's chance of winning at craps is independent of her previous record of wins and losses. If you don't invoke the definition of statistical independence, then you haven't proposed a test.

8. A blindfolded person fires a gun at a circular target of radius $b$, and is allowed to continue firing until a shot actually hits it. Any part of the target is equally likely to get hit. We measure the random distance $r$ from the center of the circle to where the bullet went in.
(a) Show that the probability distribution of $r$ must be of the form $D(r)=kr$, where $k$ is some constant. (Of course we have $D(r)=0$ for $r>b$.)
(b) Determine $k$ by requiring $D$ to be properly normalized.(answer check available at lightandmatter.com)

(c) Find the average value of $r$.(answer check available at lightandmatter.com)

(d) Interpreting your result from part c, how does it compare with $b/2$? Does this make sense? Explain.

9. We are given some atoms of a certain radioactive isotope, with half-life $t_{1/2}$. We pick one atom at random, and observe it for one half-life, starting at time zero. If it decays during that one-half-life period, we record the time $t$ at which the decay occurred. If it doesn't, we reset our clock to zero and keep trying until we get an atom that cooperates. The final result is a time $0\le t\le t_{1/2}$, with a distribution that looks like the usual exponential decay curve, but with its tail chopped off.
(a) Find the distribution $D(t)$, with the proper normalization.(answer check available at lightandmatter.com)

(b) Find the average value of $t$.(answer check available at lightandmatter.com)

(c) Interpreting your result from part b, how does it compare with $t_{1/2}/2$? Does this make sense? Explain.

10. The speed, $v$, of an atom in an ideal gas has a probability distribution of the form $D(v) = bve^{-cv^2}$, where $0\le v \lt \infty$, $c$ relates to the temperature, and $b$ is determined by normalization.
(a) Sketch the distribution.
(b) Find $b$ in terms of $c$.(answer check available at lightandmatter.com)

(c) Find the average speed in terms of $c$, eliminating $b$. (Don't try to do the indefinite integral, because it can't be done in closed form. The relevant definite integral can be found in tables or done with computer software.)(answer check available at lightandmatter.com)

11. All helium on earth is from the decay of naturally occurring heavy radioactive elements such as uranium. Each alpha particle that is emitted ends up claiming two electrons, which makes it a helium atom. If the original $^{238}\text{U}$ atom is in solid rock (as opposed to the earth's molten regions), the He atoms are unable to diffuse out of the rock. This problem involves dating a rock using the known decay properties of uranium 238. Suppose a geologist finds a sample of hardened lava, melts it in a furnace, and finds that it contains 1230 mg of uranium and 2.3 mg of helium. $^{238}\text{U}$ decays by alpha emission, with a half-life of $4.5\times10^9$ years. The subsequent chain of alpha and electron (beta) decays involves much shorter half-lives, and terminates in the stable nucleus $^{206}\text{Pb}$. Almost all natural uranium is $^{238}\text{U}$, and the chemical composition of this rock indicates that there were no decay chains involved other than that of $^{238}\text{U}$.
(a) How many alphas are emitted per decay chain? [Hint: Use conservation of mass.]
(b) How many electrons are emitted per decay chain? [Hint: Use conservation of charge.]
(c) How long has it been since the lava originally hardened?(answer check available at lightandmatter.com)

12. When light is reflected from a mirror, perhaps only 80% of the energy comes back. One could try to explain this in two different ways: (1) 80% of the photons are reflected, or (2) all the photons are reflected, but each loses 20% of its energy. Based on your everyday knowledge about mirrors, how can you tell which interpretation is correct? [Based on a problem from PSSC Physics.]

13. Suppose we want to build an electronic light sensor using an apparatus like the one described in the section on the photoelectric effect. How would its ability to detect different parts of the spectrum depend on the type of metal used in the capacitor plates?

14. The photoelectric effect can occur not just for metal cathodes but for any substance, including living tissue. Ionization of DNA molecules can cause cancer or birth defects. If the energy required to ionize DNA is on the same order of magnitude as the energy required to produce the photoelectric effect in a metal, which of the following types of electromagnetic waves might pose such a hazard? Explain.

60 Hz waves from power lines

100 MHz FM radio

microwaves from a microwave oven

visible light

ultraviolet light

x-rays

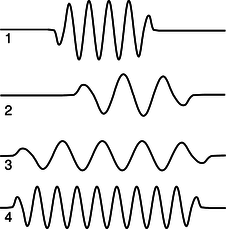
b / Problem 15.

15. (a) Rank-order the photons according to their wavelengths, frequencies, and energies. If two are equal, say so. Explain all your answers.
(b) Photon 3 was emitted by a xenon atom going from its second-lowest-energy state to its lowest-energy state. Which of photons 1, 2, and 4 are capable of exciting a xenon atom from its lowest-energy state to its second-lowest-energy state? Explain.

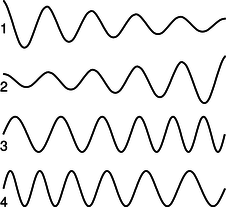
c / Problem 16.

16. Which figure could be an electron speeding up as it moves to the right? Explain.

17. The beam of a 100-W overhead projector covers an area of $1\ \text{m}\times1\ \text{m}$ when it hits the screen 3 m away. Estimate the number of photons that are in flight at any given time. (Since this is only an estimate, we can ignore the fact that the beam is not parallel.)(answer check available at lightandmatter.com)

18. In the photoelectric effect, electrons are observed with virtually no time delay ( $\sim10$ ns), even when the light source is very weak. (A weak light source does however only produce a small number of ejected electrons.) The purpose of this problem is to show that the lack of a significant time delay contradicted the classical wave theory of light, so throughout this problem you should put yourself in the shoes of a classical physicist and pretend you don't know about photons at all. At that time, it was thought that the electron might have a radius on the order of $10^{-15}$ m. (Recent experiments have shown that if the electron has any finite size at all, it is far smaller.)
(a) Estimate the power that would be soaked up by a single electron in a beam of light with an intensity of 1 $\text{mW}/\text{m}^2$.(answer check available at lightandmatter.com)
(b) The energy, $E_s$, required for the electron to escape through the surface of the cathode is on the order of $10^{-19}$ J. Find how long it would take the electron to absorb this amount of energy, and explain why your result constitutes strong evidence that there is something wrong with the classical theory.(answer check available at lightandmatter.com)

19. In a television, suppose the electrons are accelerated from rest through a voltage difference of $10^4$ V. What is their final wavelength?(answer check available at lightandmatter.com)

20. Use the Heisenberg uncertainty principle to estimate the minimum velocity of a proton or neutron in a $^{208}\text{Pb}$ nucleus, which has a diameter of about 13 fm (1 fm=$10^{-15}$ m). Assume that the speed is nonrelativistic, and then check at the end whether this assumption was warranted.(answer check available at lightandmatter.com)

21. Find the energy of a particle in a one-dimensional box of length $L$, expressing your result in terms of $L$, the particle's mass $m$, the number of peaks and valleys $n$ in the wavefunction, and fundamental constants.(answer check available at lightandmatter.com)

22. A free electron that contributes to the current in an ohmic material typically has a speed of $10^5$ m/s (much greater than the drift velocity).
(a) Estimate its de Broglie wavelength, in nm.(answer check available at lightandmatter.com)
(b) If a computer memory chip contains $10^8$ electric circuits in a 1 $\text{cm}^2$ area, estimate the linear size, in nm, of one such circuit.(answer check available at lightandmatter.com)
(c) Based on your answers from parts a and b, does an electrical engineer designing such a chip need to worry about wave effects such as diffraction?
(d) Estimate the maximum number of electric circuits that can fit on a 1 $\text{cm}^2$ computer chip before quantum-mechanical effects become important.

23. In classical mechanics, an interaction energy of the form $U(x)=\frac{1}{2}kx^2$ gives a harmonic oscillator: the particle moves back and forth at a frequency $\omega=\sqrt{k/m}$. This form for $U(x)$ is often a good approximation for an individual atom in a solid, which can vibrate around its equilibrium position at $x=0$. (For simplicity, we restrict our treatment to one dimension, and we treat the atom as a single particle rather than as a nucleus surrounded by electrons). The atom, however, should be treated quantum-mechanically, not clasically. It will have a wave function. We expect this wave function to have one or more peaks in the classically allowed region, and we expect it to tail off in the classically forbidden regions to the right and left. Since the shape of $U(x)$ is a parabola, not a series of flat steps as in figure m on page 869, the wavy part in the middle will not be a sine wave, and the tails will not be exponentials.
(a) Show that there is a solution to the Schrödinger equation of the form

$$\begin{equation*} \Psi(x)=e^{-bx^2} , \end{equation*}$$

and relate $b$ to $k$, $m$, and $\hbar$. To do this, calculate the second derivative, plug the result into the Schrödinger equation, and then find what value of $b$ would make the equation valid for all values of $x$. This wavefunction turns out to be the ground state. Note that this wavefunction is not properly normalized --- don't worry about that.(answer check available at lightandmatter.com)
(b) Sketch a graph showing what this wavefunction looks like.
(c) Let's interpret $b$. If you changed $b$, how would the wavefunction look different? Demonstrate by sketching two graphs, one for a smaller value of $b$, and one for a larger value.
(d) Making $k$ greater means making the atom more tightly bound. Mathematically, what happens to the value of $b$ in your result from part a if you make $k$ greater? Does this make sense physically when you compare with part c?

24. (a) A distance scale is shown below the wavefunctions and probability densities illustrated in figure e on page 882. Compare this with the order-of-magnitude estimate derived in subsection 13.4.4 for the radius $r$ at which the wavefunction begins tailing off. Was the estimate on the right order of magnitude?
(b) Although we normally say the moon orbits the earth, actually they both orbit around their common center of mass, which is below the earth's surface but not at its center. The same is true of the hydrogen atom. Does the center of mass lie inside the proton, or outside it?

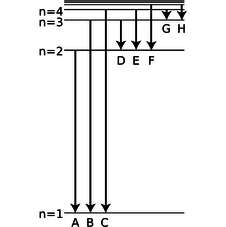
d / Problem 25.

25. The figure shows eight of the possible ways in which an electron in a hydrogen atom could drop from a higher energy state to a state of lower energy, releasing the difference in energy as a photon. Of these eight transitions, only D, E, and F produce photons with wavelengths in the visible spectrum.
(a) Which of the visible transitions would be closest to the violet end of the spectrum, and which would be closest to the red end? Explain.
(b) In what part of the electromagnetic spectrum would the photons from transitions A, B, and C lie? What about G and H? Explain.
(c) Is there an upper limit to the wavelengths that could be emitted by a hydrogen atom going from one bound state to another bound state? Is there a lower limit? Explain.

26. Find an equation for the wavelength of the photon emitted when the electron in a hydrogen atom makes a transition from energy level $n_1$ to level $n_2$.(answer check available at lightandmatter.com)

27. Estimate the angular momentum of a spinning basketball, in units of $\hbar$. Explain how this result relates to the correspondence principle.

28. Assume that the kinetic energy of an electron the $n=1$ state of a hydrogen atom is on the same order of magnitude as the absolute value of its total energy, and estimate a typical speed at which it would be moving. (It cannot really have a single, definite speed, because its kinetic and interaction energy trade off at different distances from the proton, but this is just a rough estimate of a typical speed.) Based on this speed, were we justified in assuming that the electron could be described nonrelativistically?

29. Before the quantum theory, experimentalists noted that in many cases, they would find three lines in the spectrum of the same atom that satisfied the following mysterious rule: $1/\lambda_1=1/\lambda_2+1/\lambda_3$. Explain why this would occur. Do not use reasoning that only works for hydrogen --- such combinations occur in the spectra of all elements. [Hint: Restate the equation in terms of the energies of photons.]

30. The wavefunction of the electron in the ground state of a hydrogen atom is

$$\begin{equation*} \Psi = \pi^{-1/2} a^{-3/2} e^{-r/a} , \end{equation*}$$

where $r$ is the distance from the proton, and $a=5.3\times10^{-11}$ m is a constant that sets the size of the wave.
(a) Calculate symbolically, without plugging in numbers, the probability that at any moment, the electron is inside the proton. Assume the proton is a sphere with a radius of $b=0.5$ fm. [Hint: Does it matter if you plug in $r=0$ or $r=b$ in the equation for the wavefunction?](answer check available at lightandmatter.com)
(b) Calculate the probability numerically.(answer check available at lightandmatter.com)
(c) Based on the equation for the wavefunction, is it valid to think of a hydrogen atom as having a finite size? Can $a$ be interpreted as the size of the atom, beyond which there is nothing? Or is there any limit on how far the electron can be from the proton?

31. Use physical reasoning to explain how the equation for the energy levels of hydrogen,

$$\begin{equation*} E_n = -\frac{mk^2e^4}{2\hbar^2}\cdot\frac{1}{n^2} , \end{equation*}$$

should be generalized to the case of an atom with atomic number $Z$ that has had all its electrons removed except for one.

32. A muon is a subatomic particle that acts exactly like an electron except that its mass is 207 times greater. Muons can be created by cosmic rays, and it can happen that one of an atom's electrons is displaced by a muon, forming a muonic atom. If this happens to a hydrogen atom, the resulting system consists simply of a proton plus a muon.
(a) Based on the results of section 13.4.4, how would the size of a muonic hydrogen atom in its ground state compare with the size of the normal atom?
(b) If you were searching for muonic atoms in the sun or in the earth's atmosphere by spectroscopy, in what part of the electromagnetic spectrum would you expect to find the absorption lines?

33. A photon collides with an electron and rebounds from the collision at 180 degrees, i.e., going back along the path on which it came. The rebounding photon has a different energy, and therefore a different frequency and wavelength. Show that, based on conservation of energy and momentum, the difference between the photon's initial and final wavelengths must be $2h/mc$, where $m$ is the mass of the electron. The experimental verification of this type of “pool-ball” behavior by Arthur Compton in 1923 was taken as definitive proof of the particle nature of light. Note that we're not making any nonrelativistic approximations. To keep the algebra simple, you should use natural units --- in fact, it's a good idea to use even-more-natural-than-natural units, in which we have not just $c=1$ but also $h=1$, and $m=1$ for the mass of the electron. You'll also probably want to use the relativistic relationship $E^2-p^2=m^2$, which becomes $E^2-p^2=1$ for the energy and momentum of the electron in these units.

34. Generalize the result of problem 33 to the case where the photon bounces off at an angle other than 180° with respect to its initial direction of motion.

35. On page 869 we derived an expression for the probability that a particle would tunnel through a rectangular barrier, i.e., a region in which the interaction energy $U(x)$ has a graph that looks like a rectangle. Generalize this to a barrier of any shape. [Hints: First try generalizing to two rectangular barriers in a row, and then use a series of rectangular barriers to approximate the actual curve of an arbitrary function $U(x)$. Note that the width and height of the barrier in the original equation occur in such a way that all that matters is the area under the $U$-versus-$x$ curve. Show that this is still true for a series of rectangular barriers, and generalize using an integral.] If you had done this calculation in the 1930's you could have become a famous physicist.

36. Show that the wavefunction given in problem 30 is properly normalized.

37. Show that a wavefunction of the form $\Psi = e^{by} \sin ax$ is a possible solution of the Schrödinger equation in two dimensions, with a constant potential. Can we tell whether it would apply to a classically allowed region, or a classically forbidden one?

38. Find the energy levels of a particle in a three-dimensional rectangular box with sides of length $a$, $b$, and $c$.(answer check available at lightandmatter.com)

39. Americium-241 is an artificial isotope used in smoke detectors. It undergoes alpha decay, with a half-life of 432 years. As discussed in example 18 on page 870, alpha decay can be understood as a tunneling process, and although the barrier is not rectangular in shape, the equation for the tunneling probability on page 870 can still be used as a rough guide to our thinking. For americium-241, the tunneling probability is about $1\times10^{-29}$. Suppose that this nucleus were to decay by emitting a tritium (helium-3) nucleus instead of an alpha particle (helium-4). Estimate the relevant tunneling probability, assuming that the total energy $E$ remains the same. This higher probability is contrary to the empirical observation that this nucleus is not observed to decay by tritium emission with any significant probability, and in general tritium emission is almost unknown in nature; this is mainly because the tritium nucleus is far less stable than the helium-4 nucleus, and the difference in binding energy reduces the energy available for the decay.

40. As far as we know, the mass of the photon is zero. However, it's not possible to prove by experiments that anything is zero; all we can do is put an upper limit on the number. As of 2008, the best experimental upper limit on the mass of the photon is about $1\times 10^{-52}$ kg. Suppose that the photon's mass really isn't zero, and that the value is at the top of the range that is consistent with the present experimental evidence. In this case, the $c$ occurring in relativity would no longer be interpreted as the speed of light. As with material particles, the speed $v$ of a photon would depend on its energy, and could never be as great as $c$. Estimate the relative size $(c-v)/c$ of the discrepancy in speed, in the case of a photon with a frequency of 1 kHz, lying in the very low frequency radio range. \hwans{hwans:photon-mass}

41. Hydrogen is the only element whose energy levels can be expressed exactly in an equation. Calculate the ratio $\lambda_E/\lambda_F$ of the wavelengths of the transitions labeled E and F in problem 25 on p. 898. Express your answer as an exact fraction, not a decimal approximation. In an experiment in which atomic wavelengths are being measured, this ratio provides a natural, stringent check on the precision of the results.(answer check available at lightandmatter.com)

42. Give a numerical comparison of the number of photons per second emitted by a hundred-watt FM radio transmitter and a hundred-watt lightbulb.(answer check available at lightandmatter.com)

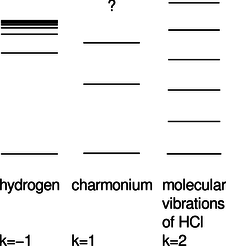
e / Problem 43.

43. On pp. 884-885 of subsection 13.4.4, we used simple algebra to derive an approximate expression for the energies of states in hydrogen, without having to explicitly solve the Schrödinger equation. As input to the calculation, we used the the proportionality $U \propto r^{-1}$, which is a characteristic of the electrical interaction. The result for the energy of the $n$th standing wave pattern was $E_n \propto n^{-2}$.

There are other systems of physical interest in which we have $U \propto r^k$ for values of $k$ besides $-1$. Problem 23 discusses the ground state of the harmonic oscillator, with $k=2$ (and a positive constant of proportionality). In particle physics, systems called charmonium and bottomonium are made out of pairs of subatomic particles called quarks, which interact according to $k=1$, i.e., a force that is independent of distance. (Here we have a positive constant of proportionality, and $r>0$ by definition. The motion turns out not to be too relativistic, so the Schrödinger equation is a reasonable approximation.) The figure shows actual energy levels for these three systems, drawn with different energy scales so that they can all be shown side by side. The sequence of energies in hydrogen approaches a limit, which is the energy required to ionize the atom. In charmonium, only the first three levels are known.⁸

Generalize the method used for $k=-1$ to any value of $k$, and find the exponent $j$ in the resulting proportionality $E_n \propto n^j$. Compare the theoretical calculation with the behavior of the actual energies shown in the figure. Comment on the limit $k\rightarrow\infty$. (answer check available at lightandmatter.com)

44. The electron, proton, and neutron were discovered, respectively, in 1897, 1919, and 1932. The neutron was late to the party, and some physicists felt that it was unnecessary to consider it as fundamental. Maybe it could be explained as simply a proton with an electron trapped inside it. The charges would cancel out, giving the composite particle the correct neutral charge, and the masses at least approximately made sense (a neutron is heavier than a proton). (a) Given that the diameter of a proton is on the order of $10^{-15}\ \text{m}$, use the Heisenberg uncertainty principle to estimate the trapped electron's minimum momentum.(answer check available at lightandmatter.com)
(b) Find the electron's minimum kinetic energy.(answer check available at lightandmatter.com)
(c) Show via $E=mc^2$ that the proposed explanation fails, because the contribution to the neutron's mass from the electron's kinetic energy would be many orders of magnitude too large.

45. Suppose that an electron, in one dimension, is confined to a certain region of space so that its wavefunction is given by

$$\begin{equation*} \Psi = \begin{cases} 0 & \text{if } x\lt0 \\ A \sin(2\pi x/L) & \text{if } 0\le x\le L \\ 0 & \text{if } x>L \end{cases} \end{equation*}$$

Determine the constant $A$ from normalization.(answer check available at lightandmatter.com)

46. In the following, $x$ and $y$ are variables, while $u$ and $v$ are constants. Compute (a) $\partial(ux\ln (vy))/\partial x$, (b) $\partial(ux\ln (vy))/\partial y$.(answer check available at lightandmatter.com)

47. (a) A radio transmitter radiates power $P$ in all directions, so that the energy spreads out spherically. Find the energy density at a distance $r$.(answer check available at lightandmatter.com)
(b) Let the wavelength be $\lambda$. As described in example 8 on p. 842, find the number of photons in a volume $\lambda^3$ at this distance $r$.(answer check available at lightandmatter.com)
(c) For a 1000 kHz AM radio transmitting station, assuming reasonable values of $P$ and $r$, verify, as claimed in the example, that the result from part b is very large.

Benjamin Crowell (Fullerton College). Conceptual Physics is copyrighted with a CC-BY-SA license.