11.1: Fields of Force

Cutting-edge science readily infiltrates popular culture, though sometimes in garbled form. The Newtonian imagination populated the universe mostly with that nice solid stuff called matter, which was made of little hard balls called atoms. In the early twentieth century, consumers of pulp fiction and popularized science began to hear of a new image of the universe, full of x-rays, N-rays, and Hertzian waves. What they were beginning to soak up through their skins was a drastic revision of Newton's concept of a universe made of chunks of matter which happened to interact via forces. In the newly emerging picture, the universe was made of force, or, to be more technically accurate, of ripples in universal fields of force. Unlike the average reader of Cosmic Stories in 1941, you now possess enough technical background to understand what a “force field” really is.

10.1.1 Why fields?

Time delays in forces exerted at a distance

What convinced physicists that they needed this new concept of a field of force? Although we have been dealing mostly with electrical forces, let's start with a magnetic example. (In fact the main reason I've delayed a detailed discussion of magnetism for so long is that mathematical calculations of magnetic effects are handled much more easily with the concept of a field of force.) First a little background leading up to our example.

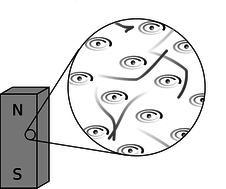
a / A bar magnet's atoms are (partially) aligned.

A bar magnet, a, has an axis about which many of the electrons' orbits are oriented. The earth itself is also a magnet, although not a bar-shaped one.

b / A bar magnet interacts with our magnetic planet.

The interaction between the earth-magnet and the bar magnet, b, makes them want to line up their axes in opposing directions (in other words such that their electrons rotate in parallel planes, but with one set rotating clockwise and the other counterclockwise as seen looking along the axes).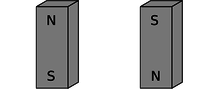

c / Magnets aligned north-south.

On a smaller scale, any two bar magnets placed near each other will try to align themselves head-to-tail, c.

Now we get to the relevant example. It is clear that two people separated by a paper-thin wall could use a pair of bar magnets to signal to each other. Each person would feel her own magnet trying to twist around in response to any rotation performed by the other person's magnet. The practical range of communication would be very short for this setup, but a sensitive electrical apparatus could pick up magnetic signals from much farther away. In fact, this is not so different from what a radio does: the electrons racing up and down the transmitting antenna create forces on the electrons in the distant receiving antenna. (Both magnetic and electric forces are involved in real radio signals, but we don't need to worry about that yet.)

A question now naturally arises as to whether there is any time delay in this kind of communication via magnetic (and electric) forces. Newton would have thought not, since he conceived of physics in terms of instantaneous action at a distance. We now know, however, that there is such a time delay. If you make a long-distance phone call that is routed through a communications satellite, you should easily be able to detect a delay of about half a second over the signal's round trip of 50,000 miles. Modern measurements have shown that electric, magnetic, and gravitational forces all travel at the speed of light, \(3\times10^8\) m/s. (In fact, we will soon discuss how light itself is made of electricity and magnetism.)

If it takes some time for forces to be transmitted through space, then apparently there is some thing that travels through space. The fact that the phenomenon travels outward at the same speed in all directions strongly evokes wave metaphors such as ripples on a pond.

More evidence that fields of force are real: they carry energy.

The smoking-gun argument for this strange notion of traveling force ripples comes from the fact that they carry energy.

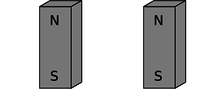
d / The second magnet is reversed.

First suppose that the person holding the bar magnet on the right decides to reverse hers, resulting in configuration d. She had to do mechanical work to twist it, and if she releases the magnet, energy will be released as it flips back to c. She has apparently stored energy by going from c to d. So far everything is easily explained without the concept of a field of force.

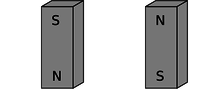
e / Both magnets are reversed.

But now imagine that the two people start in position c and then simultaneously flip their magnets extremely quickly to position e, keeping them lined up with each other the whole time. Imagine, for the sake of argument, that they can do this so quickly that each magnet is reversed while the force signal from the other is still in transit. (For a more realistic example, we'd have to have two radio antennas, not two magnets, but the magnets are easier to visualize.) During the flipping, each magnet is still feeling the forces arising from the way the other magnet used to be oriented. Even though the two magnets stay aligned during the flip, the time delay causes each person to feel resistance as she twists her magnet around. How can this be? Both of them are apparently doing mechanical work, so they must be storing magnetic energy somehow. But in the traditional Newtonian conception of matter interacting via instantaneous forces at a distance, interaction energy arises from the relative positions of objects that are interacting via forces. If the magnets never changed their orientations relative to each other, how can any magnetic energy have been stored?

The only possible answer is that the energy must have gone into the magnetic force ripples crisscrossing the space between the magnets. Fields of force apparently carry energy across space, which is strong evidence that they are real things.

This is perhaps not as radical an idea to us as it was to our ancestors. We are used to the idea that a radio transmitting antenna consumes a great deal of power, and somehow spews it out into the universe. A person working around such an antenna needs to be careful not to get too close to it, since all that energy can easily cook flesh (a painful phenomenon known as an “RF burn”).

10.1.2 The gravitational field

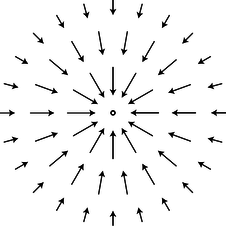
Given that fields of force are real, how do we define, measure, and calculate them? A fruitful metaphor will be the wind patterns experienced by a sailing ship. Wherever the ship goes, it will feel a certain amount of force from the wind, and that force will be in a certain direction. The weather is ever-changing, of course, but for now let's just imagine steady wind patterns. Definitions in physics are operational, i.e., they describe how to measure the thing being defined. The ship's captain can measure the wind's “field of force” by going to the location of interest and determining both the direction of the wind and the strength with which it is blowing. Charting all these measurements on a map leads to a depiction of the field of wind force like the one shown in the figure. This is known as the “sea of arrows” method of visualizing a field.

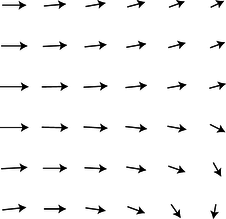
f / The wind patterns in a certain area of the ocean could be charted in a “sea of arrows” representation like this. Each arrow represents both the wind's strength and its direction at a certain location.

Now let's see how these concepts are applied to the fundamental force fields of the universe. We'll start with the gravitational field, which is the easiest to understand. As with the wind patterns, we'll start by imagining gravity as a static field, even though the existence of the tides proves that there are continual changes in the gravity field in our region of space. When the gravitational field was introduced in chapter 2, I avoided discussing its direction explicitly, but defining it is easy enough: we simply go to the location of interest and measure the direction of the gravitational force on an object, such as a weight tied to the end of a string.

In chapter 2, I defined the gravitational field in terms of the energy required to raise a unit mass through a unit distance. However, I'm going to give a different definition now, using an approach that will be more easily adapted to electric and magnetic fields. This approach is based on force rather than energy. We couldn't carry out the energy-based definition without dividing by the mass of the object involved, and the same is true for the force-based definition. For example, gravitational forces are weaker on the moon than on the earth, but we cannot specify the strength of gravity simply by giving a certain number of newtons. The number of newtons of gravitational force depends not just on the strength of the local gravitational field but also on the mass of the object on which we're testing gravity, our “test mass.” A boulder on the moon feels a stronger gravitational force than a pebble on the earth. We can get around this problem by defining the strength of the gravitational field as the force acting on an object, divided by the object's mass:

The gravitational field vector, \(\mathbf{g}\), at any location in space is found by placing a test mass \(m_t\) at that point. The field vector is then given by \(\mathbf{g}=\mathbf{F}/m_t\), where \(\mathbf{F}\) is the gravitational force on the test mass.

We now have three ways of representing a gravitational field. The magnitude of the gravitational field near the surface of the earth, for instance, could be written as 9.8 N/kg, 9.8 \(\text{J}/\text{kg}\cdot\text{m}\), or 9.8 \(\text{m}/\text{s}^2\). If we already had two names for it, why invent a third? The main reason is that it prepares us with the right approach for defining other fields.

The most subtle point about all this is that the gravitational field tells us about what forces would be exerted on a test mass by the earth, sun, moon, and the rest of the universe, if we inserted a test mass at the point in question. The field still exists at all the places where we didn't measure it.

Example 1: Gravitational field of the earth

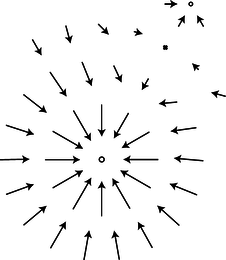
\(\triangleright\) What is the magnitude of the earth's gravitational field, in terms of its mass, \(M\), and the distance \(r\) from its center? g / The gravitational field surrounding a clump of mass such as the earth. \(\triangleright\) Substituting \(|\mathbf{F}|= GMm_{t}/ r^2\) into the definition of the gravitational field, we find \(|\mathbf{g}|= GM/ r^2\). This expression could be used for the field of any spherically symmetric mass distribution, since the equation we assumed for the gravitational force would apply in any such case.

Sources and sinks

If we make a sea-of-arrows picture of the gravitational fields surrounding the earth, g, the result is evocative of water going down a drain. For this reason, anything that creates an inward-pointing field around itself is called a sink. The earth is a gravitational sink. The term “source” can refer specifically to things that make outward fields, or it can be used as a more general term for both “outies” and “innies.” However confusing the terminology, we know that gravitational fields are only attractive, so we will never find a region of space with an outward-pointing field pattern.

Knowledge of the field is interchangeable with knowledge of its sources (at least in the case of a static, unchanging field). If aliens saw the earth's gravitational field pattern they could immediately infer the existence of the planet, and conversely if they knew the mass of the earth they could predict its influence on the surrounding gravitational field.

Superposition of indexsuperposition of fieldsindexfieldssuperposition offields

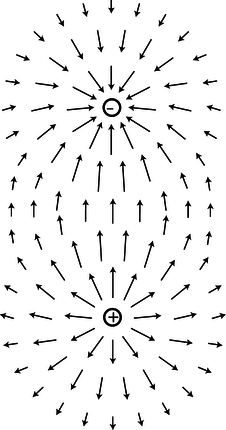
h / The gravitational fields of the earth and moon superpose. Note how the fields cancel at one point, and how there is no boundary between the interpenetrating fields surrounding the two bodies.

A very important fact about all fields of force is that when there is more than one source (or sink), the fields add according to the rules of vector addition. The gravitational field certainly will have this property, since it is defined in terms of the force on a test mass, and forces add like vectors. Superposition is an important characteristics of waves, so the superposition property of fields is consistent with the idea that disturbances can propagate outward as waves in a field.

Example 2: Reduction in gravity on Io due to Jupiter's gravity

\(\triangleright\) The average gravitational field on Jupiter's moon Io is 1.81 N/kg. By how much is this reduced when Jupiter is directly overhead? Io's orbit has a radius of \( 4.22\times10^8\) m, and Jupiter's mass is \( 1.899\times10^{27}\) kg. \(\triangleright\) By the shell theorem, we can treat the Jupiter as if its mass was all concentrated at its center, and likewise for Io. If we visit Io and land at the point where Jupiter is overhead, we are on the same line as these two centers, so the whole problem can be treated one-dimensionally, and vector addition is just like scalar addition. Let's use positive numbers for downward fields (toward the center of Io) and negative for upward ones. Plugging the appropriate data into the expression derived in example 1, we find that the Jupiter's contribution to the field is \(- 0.71\) N/kg. Superposition says that we can find the actual gravitational field by adding up the fields created by Io and Jupiter: \(1.81-0.71\) N/kg = 1.1 N/kg. You might think that this reduction would create some spectacular effects, and make Io an exciting tourist destination. Actually you would not detect any difference if you flew from one side of Io to the other. This is because your body and Io both experience Jupiter's gravity, so you follow the same orbital curve through the space around Jupiter.

i / The part of the LIGO gravity wave detector at Hanford Nuclear Reservation, near Richland, Washington. The other half of the detector is in Louisiana.

Gravitational waves

A source that sits still will create a static field pattern, like a steel ball sitting peacefully on a sheet of rubber. A moving source will create a spreading wave pattern in the field, like a bug thrashing on the surface of a pond. Although we have started with the gravitational field as the simplest example of a static field, stars and planets do more stately gliding than thrashing, so gravitational waves are not easy to detect. Newton's theory of gravity does not describe gravitational waves, but they are predicted by Einstein's general theory of relativity. J.H. Taylor and R.A. Hulse were awarded the Nobel Prize in 1993 for giving indirect evidence that Einstein's waves actually exist. They discovered a pair of exotic, ultra-dense stars called neutron stars orbiting one another very closely, and showed that they were losing orbital energy at the rate predicted by Einstein's theory.

A Caltech-MIT collaboration has built a pair of gravitational wave detectors called LIGO to search for more direct evidence of gravitational waves. Since they are essentially the most sensitive vibration detectors ever made, they are located in quiet rural areas, and signals will be compared between them to make sure that they were not due to passing trucks. The project began operating at full sensitivity in 2005, and is now able to detect a vibration that causes a change of \(10^{-18}\) m in the distance between the mirrors at the ends of the 4-km vacuum tunnels. This is a thousand times less than the size of an atomic nucleus! There is only enough funding to keep the detectors operating for a few more years, so the physicists can only hope that during that time, somewhere in the universe, a sufficiently violent cataclysm will occur to make a detectable gravitational wave. (More accurately, they want the wave to arrive in our solar system during that time, although it will have been produced millions of years before.)

10.1.3 The electric field

Definition

The definition of the electric field is directly analogous to, and has the same motivation as, the definition of the gravitational field:

The electric field vector, \(\mathbf{E}\), at any location in space is found by placing a test charge \(q_t\) at that point. The electric field vector is then given by \(\mathbf{E}=\mathbf{F}/q_t\), where \(\mathbf{F}\) is the electric force on the test charge.

Charges are what create electric fields. Unlike gravity, which is always attractive, electricity displays both attraction and repulsion. A positive charge is a source of electric fields, and a negative one is a sink.

The most difficult point about the definition of the electric field is that the force on a negative charge is in the opposite direction compared to the field. This follows from the definition, since dividing a vector by a negative number reverses its direction. It's as though we had some objects that fell upward instead of down.

self-check:

Find an equation for the magnitude of the field of a single point charge \(Q\).

(answer in the back of the PDF version of the book)

Example 3: Superposition of electric fields

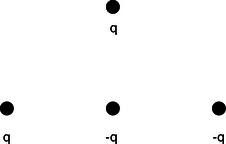
\(\triangleright\) Charges \(q\) and \(- q\) are at a distance \(b\) from each other, as shown in the figure. What is the electric field at the point P, which lies at a third corner of the square? j / Example 3. \(\triangleright\) The field at P is the vector sum of the fields that would have been created by the two charges independently. Let positive \(x\) be to the right and let positive \(y\) be up. Negative charges have fields that point at them, so the charge \(-q\) makes a field that points to the right, i.e., has a positive \(x\) component. Using the answer to the self-check, we have \[\begin{align*} E_{-q,x} &= \frac{ kq}{ b^2} \\ E_{-q,y} &= 0 . \end{align*}\] Note that if we had blindly ignored the absolute value signs and plugged in \(- q\) to the equation, we would have incorrectly concluded that the field went to the left. By the Pythagorean theorem, the positive charge is at a distance \(\sqrt{2} b\) from P, so the magnitude of its contribution to the field is \(E= kq/2 b^2\). Positive charges have fields that point away from them, so the field vector is at an angle of 135° counterclockwise from the \(x\) axis. \[\begin{align*} E_{q,x} &= \frac{ kq}{2 b^2} \text{cos}\ 135° \\ &= -\frac{ kq}{2^\text{3/2} b^2} \\ E_{q,y} &= \frac{ kq}{2 b^2} \text{sin}\ 135° \\ &= \frac{ kq}{2^\text{3/2} b^2} \end{align*}\] The total field is \[\begin{align*} E_\text{x} &= \left(1-2^{-\text{3/2}}\right)\frac{ kq}{ b^2} \\ E_{y} &= \frac{ kq}{2^\text{3/2} b^2} \end{align*}\]

Dipoles

k / A dipole field. Electric fields diverge from a positive charge and converge on a negative charge.

The simplest set of sources that can occur with electricity but not with gravity is the dipole, consisting of a positive charge and a negative charge with equal magnitudes. More generally, an electric dipole can be any object with an imbalance of positive charge on one side and negative on the other.

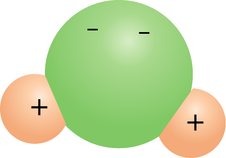
l / A water molecule is a dipole.

A water molecule, l, is a dipole because the electrons tend to shift away from the hydrogen atoms and onto the oxygen atom.

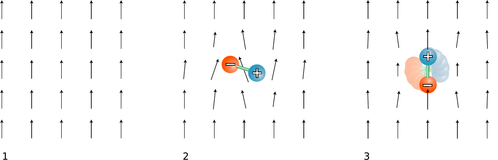
m / 1. A uniform electric field created by some charges “off-stage.” 2. A dipole is placed in the field. 3. The dipole aligns with the field.

Your microwave oven acts on water molecules with electric fields. Let us imagine what happens if we start with a uniform electric field, m/1, made by some external charges, and then insert a dipole, m/2, consisting of two charges connected by a rigid rod. The dipole disturbs the field pattern, but more important for our present purposes is that it experiences a torque. In this example, the positive charge feels an upward force, but the negative charge is pulled down. The result is that the dipole wants to align itself with the field, m/3. The microwave oven heats food with electrical (and magnetic) waves. The alternation of the torque causes the molecules to wiggle and increase the amount of random motion. The slightly vague definition of a dipole given above can be improved by saying that a dipole is any object that experiences a torque in an electric field.

What determines the torque on a dipole placed in an externally created field? Torque depends on the force, the distance from the axis at which the force is applied, and the angle between the force and the line from the axis to the point of application. Let a dipole consisting of charges \(+q\) and \(-q\) separated by a distance \(\ell\) be placed in an external field of magnitude \(|\mathbf{E}|\), at an angle \(\theta\) with respect to the field. The total torque on the dipole is

\[\begin{align*} \tau &= \frac{\ell}{2}q|\mathbf{E}|\sin \theta+\frac{\ell}{2}q|\mathbf{E}|\sin \theta \\ &= \ell q|\mathbf{E}|\sin \theta . \end{align*}\]

(Note that even though the two forces are in opposite directions, the torques do not cancel, because they are both trying to twist the dipole in the same direction.) The quantity is called the dipole moment, notated \(D\). (More complex dipoles can also be assigned a dipole moment --- they are defined as having the same dipole moment as the two-charge dipole that would experience the same torque.)

Employing a little more mathematical elegance, we can define a dipole moment vector,

\[\begin{equation*} \mathbf{D} = \sum q_i \mathbf{r}_i , \end{equation*}\]

where \(\mathbf{r}_i\) is the position vector of the charge labeled by the index \(i\). We can then write the torque in terms of a vector cross product (page 281),

\[\begin{equation*} \boldsymbol{\tau} = \mathbf{D}\times\mathbf{E} . \end{equation*}\]

No matter how we notate it, the definition of the dipole moment requires that we choose point from which we measure all the position vectors of the charges. However, in the commonly encountered special case where the total charge of the object is zero, the dipole moment is the same regardless of this choice.

Example 4: Dipole moment of a molecule of NaCl gas

\(\triangleright\) In a molecule of NaCl gas, the center-to-center distance between the two atoms is about 0.6 nm. Assuming that the chlorine completely steals one of the sodium's electrons, compute the magnitude of this molecule's dipole moment. \(\triangleright\) The total charge is zero, so it doesn't matter where we choose the origin of our coordinate system. For convenience, let's choose it to be at one of the atoms, so that the charge on that atom doesn't contribute to the dipole moment. The magnitude of the dipole moment is then \[\begin{align*} D &= (6\times10^{-10}\ \text{m})( e) \\ &= (6\times10^{-10}\ \text{m})( 1.6\times10^{-19}\ \text{C}) \\ &= 1\times10^{-28}\ \text{C}\cdot\text{m} \end{align*}\]

Example 5: Dipole moments as vectors

\(\triangleright\) The horizontal and vertical spacing between the charges in the figure is \(b\). Find the dipole moment. n / Example 5. \(\triangleright\) Let the origin of the coordinate system be at the leftmost charge. \[\begin{align*} \mathbf{D} &= \sum q_i \mathbf{r}_i \\ &= (q)(\text{0})+(-q)(b\hat{\mathbf{x}})+(q)(b\hat{\mathbf{x}}+b\hat{\mathbf{y}})+(-q)(2b\hat{\mathbf{x}}) \\ &= -2bq\hat{\mathbf{x}}+bq\hat{\mathbf{y}} \end{align*}\]

Alternative definition of the electric field

The behavior of a dipole in an externally created field leads us to an alternative definition of the electric field:

The electric field vector, \(E\), at any location in space is defined by observing the torque exerted on a test dipole \(D_t\) placed there. The direction of the field is the direction in which the field tends to align a dipole (from \(-\) to +), and the field's magnitude is \(|\mathbf{E}|=\tau/D_t\sin\theta\). In other words, the field vector is the vector that satisfies the equation \(\boldsymbol{\tau} = \mathbf{D}_t\times\mathbf{E}\) for any test dipole \(\mathbf{D}_t\) placed at that point in space.

The main reason for introducing a second definition for the same concept is that the magnetic field is most easily defined using a similar approach.

Discussion Questions

◊ In the definition of the electric field, does the test charge need to be 1 coulomb? Does it need to be positive?

◊ Does a charged particle such as an electron or proton feel a force from its own electric field?

◊ Is there an electric field surrounding a wall socket that has nothing plugged into it, or a battery that is just sitting on a table?

◊ In a flashlight powered by a battery, which way do the electric fields point? What would the fields be like inside the wires? Inside the filament of the bulb?

◊ Criticize the following statement: “An electric field can be represented by a sea of arrows showing how current is flowing.”

◊ The field of a point charge, \(|\mathbf{E}|=kQ/r^2\), was derived in a self-check. How would the field pattern of a uniformly charged sphere compare with the field of a point charge?

◊ The interior of a perfect electrical conductor in equilibrium must have zero electric field, since otherwise the free charges within it would be drifting in response to the field, and it would not be in equilibrium. What about the field right at the surface of a perfect conductor? Consider the possibility of a field perpendicular to the surface or parallel to it.

◊ Compare the dipole moments of the molecules and molecular ions shown in the figure.

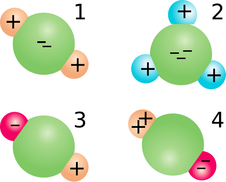
o / Discussion question H.

◊ Small pieces of paper that have not been electrically prepared in any way can be picked up with a charged object such as a charged piece of tape. In our new terminology, we could describe the tape's charge as inducing a dipole moment in the paper. Can a similar technique be used to induce not just a dipole moment but a charge?

Contributors

Benjamin Crowell (Fullerton College). Conceptual Physics is copyrighted with a CC-BY-SA license.