12.1: More About the Magnetic Field
( \newcommand{\kernel}{\mathrm{null}\,}\)
11.1.1 Magnetic forces
In this chapter, I assume you know a few basic ideas about Einstein's theory of relativity, as described in sections 7.1 and 7.2. Unless your typical workday involves rocket ships or particle accelerators, all this relativity stuff might sound like a description of some bizarre futuristic world that is completely hypothetical. There is, however, a relativistic effect that occurs in everyday life, and it is obvious and dramatic: magnetism. Magnetism, as we discussed previously, is an interaction between a moving charge and another moving charge, as opposed to electric forces, which act between any pair of charges, regardless of their motion. Relativistic effects are weak for speeds that are small compared to the speed of light, and the average speed at which electrons drift through a wire is quite low (centimeters per second, typically), so how can relativity be behind an impressive effect like a car being lifted by an electromagnet hanging from a crane? The key is that matter is almost perfectly electrically neutral, and electric forces therefore cancel out almost perfectly. Magnetic forces really aren't very strong, but electric forces are even weaker.
What about the word “relativity” in the name of the theory? It would seem problematic if moving charges interact differently than stationary charges, since motion is a matter of opinion, depending on your frame of reference. Magnetism, however, comes not to destroy relativity but to fulfill it. Magnetic interactions must exist according to the theory of relativity. To understand how this can be, consider how time and space behave in relativity. Observers in different frames of reference disagree about the lengths of measuring sticks and the speeds of clocks, but the laws of physics are valid and self-consistent in either frame of reference. Similarly, observers in different frames of reference disagree about what electric and magnetic fields and forces there are, but they agree about concrete physical events.
a / The pair of charged particles, as seen in two different frames of reference.
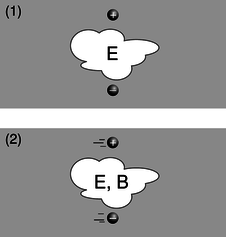
For instance, figure a/1 shows two particles, with opposite charges, which are not moving at a particular moment in time. An observer in this frame of reference says there are electric fields around the particles, and predicts that as time goes on, the particles will begin to accelerate towards one another, eventually colliding. A different observer, a/2, says the particles are moving. This observer also predicts that the particles will collide, but explains their motion in terms of both an electric field, E, and a magnetic field, B. As we'll see shortly, the magnetic field is required in order to maintain consistency between the predictions made in the two frames of reference.
To see how this really works out, we need to find a nice simple example that is easy to calculate. An example like figure a is not easy to handle, because in the second frame of reference, the moving charges create fields that change over time at any given location. Examples like figure b are easier, because there is a steady flow of charges, and all the fields stay the same over time.1 What is remarkable about this demonstration is that there can be no electric fields acting on the electron beam at all, since the total charge density throughout the wire is zero. Unlike figure a/2, figure b is purely magnetic.
b / A large current is created by shorting across the leads of the battery. The moving charges in the wire attract the moving charges in the electron beam, causing the electrons to curve.
To see why this must occur based on relativity, we make the mathematically idealized model shown in figure c.
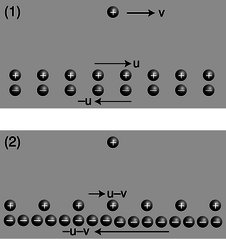
c / A charged particle and a current, seen in two different frames of reference. The second frame is moving at velocity v with respect to the first frame, so all the velocities have v subtracted from them. (As discussed in the main text, this is only approximately correct.)
The charge by itself is like one of the electrons in the vacuum tube beam of figure b, and a pair of moving, infinitely long line charges has been substituted for the wire. The electrons in a real wire are in rapid thermal motion, and the current is created only by a slow drift superimposed on this chaos. A second deviation from reality is that in the real experiment, the protons are at rest with respect to the tabletop, and it is the electrons that are in motion, but in c/1 we have the positive charges moving in one direction and the negative ones moving the other way. If we wanted to, we could construct a third frame of reference in which the positive charges were at rest, which would be more like the frame of reference fixed to the tabletop in the real demonstration. However, as we'll see shortly, frames c/1 and c/2 are designed so that they are particularly easy to analyze. It's important to note that even though the two line charges are moving in opposite directions, their currents don't cancel. A negative charge moving to the left makes a current that goes to the right, so in frame c/1, the total current is twice that contributed by either line charge.
Frame 1 is easy to analyze because the charge densities of the two line charges cancel out, and the electric field experienced by the lone charge is therefore zero:
In frame 1, any force experienced by the lone charge must therefore be attributed solely to magnetism.
Frame 2 shows what we'd see if we were observing all this from a frame of reference moving along with the lone charge. Why don't the charge densities also cancel in this frame? Here's where the relativity comes in. Relativity tells us that moving objects appear contracted to an observer who is not moving along with them. Both line charges are in motion in both frames of reference, but in frame 1, the line charges were moving at equal speeds, so their contractions were equal, and their charge densities canceled out. In frame 2, however, their speeds are unequal. The positive charges are moving more slowly than in frame 1, so in frame 2 they are less contracted. The negative charges are moving more quickly, so their contraction is greater now. Since the charge densities don't cancel, there is an electric field in frame 2, which points into the wire, attracting the lone charge. Furthermore, the attraction felt by the lone charge must be purely electrical, since the lone charge is at rest in this frame of reference, and magnetic effects occur only between moving charges and other moving charges.2
To summarize, frame 1 displays a purely magnetic attraction, while in frame 2 it is purely electrical.
Now we can calculate the force in frame 2, and equating it to the force in frame 1, we can find out how much magnetic force occurs. To keep the math simple, and to keep from assuming too much about your knowledge of relativity, we're going to carry out this whole calculation in the approximation where all the speeds are fairly small compared to the speed of light.3 For instance, if we find an expression such as (v/c)2+(v/c)4, we will assume that the fourth-order term is negligible by comparison. This is known as a calculation “to leading order in v/c.” In fact, I've already used the leading-order approximation twice without saying so! The first time I used it implicitly was in figure c, where I assumed that the velocities of the two line charges were u−v and −u−v. Relativistic velocities don't just combine by simple addition and subtraction like this, but this is an effect we can ignore in the present approximation. The second sleight of hand occurred when I stated that we could equate the forces in the two frames of reference. Force, like time and distance, is distorted relativistically when we change from one frame of reference to another. Again, however, this is an effect that we can ignore to the desired level of approximation.
Let ±λ be the charge per unit length of each line charge without relativistic contraction, i.e., in the frame moving with that line charge. Using the approximation γ=(1−v2/c2)−1/2≈1+v2/2c2 for v≪c, the total charge per unit length in frame 2 is
Let R be the distance from the line charge to the lone charge. Applying Gauss' law to a cylinder of radius R centered on the line charge, we find that the magnitude of the electric field experienced by the lone charge in frame 2 is
and the force acting on the lone charge q is
In frame 1, the current is I=2λ1u (see homework problem 5), which we can approximate as I=2λu, since the current, unlike λtotal, 2, doesn't vanish completely without the relativistic effect. The magnetic force on the lone charge q due to the current I is
Discussion Question
◊ Resolve the following paradox concerning the argument given in this section. We would expect that at any given time, electrons in a solid would be associated with protons in a definite way. For simplicity, let's imagine that the solid is made out of hydrogen (which actually does become a metal under conditions of very high pressure). A hydrogen atom consists of a single proton and a single electron. Even if the electrons are moving and forming an electric current, we would imagine that this would be like a game of musical chairs, with the protons as chairs and the electrons as people. Each electron has a proton that is its “friend,” at least for the moment. This is the situation shown in figure c/1. How, then, can an observer in a different frame see the electrons and protons as not being paired up, as in c/2?
11.1.2 The magnetic field
Definition in terms of the force on a moving particle
With electricity, it turned out to be useful to define an electric field rather than always working in terms of electric forces. Likewise, we want to define a magnetic field, B. Let's look at the result of the preceding subsection for insight. The equation
shows that when we put a moving charge near other moving charges, there is an extra magnetic force on it, in addition to any electric forces that may exist. Equations for electric forces always have a factor of k in front --- the Coulomb constant k is called the coupling constant for electric forces. Since magnetic effects are relativistic in origin, they end up having a factor of k/c2 instead of just k. In a world where the speed of light was infinite, relativistic effects, including magnetism, would be absent, and the coupling constant for magnetism would be zero. A cute feature of the metric system is that we have k/c2=10−7 N⋅s2/C2 exactly, as a matter of definition.
Naively, we could try to work by analogy with the electric field, and define the magnetic field as the magnetic force per unit charge. However, if we think of the lone charge in our example as the test charge, we'll find that this approach fails, because the force depends not just on the test particle's charge, but on its velocity, v, as well. Although we only carried out calculations for the case where the particle was moving parallel to the wire, in general this velocity is a vector, v, in three dimensions. We can also anticipate that the magnetic field will be a vector. The electric and gravitational fields are vectors, and we expect intuitively based on our experience with magnetic compasses that a magnetic field has a particular direction in space. Furthermore, reversing the current I in our example would have reversed the force, which would only make sense if the magnetic field had a direction in space that could be reversed. Summarizing, we think there must be a magnetic field vector B, and the force on a test particle moving through a magnetic field is proportional both to the B vector and to the particle's own v vector. In other words, the magnetic force vector F is found by some sort of vector multiplication of the vectors v and B. As proved on page 912, however, there is only one physically useful way of defining such a multiplication, which is the cross product.
We therefore define the magnetic field vector, B, as the vector that determines the force on a charged particle according to the following rule:
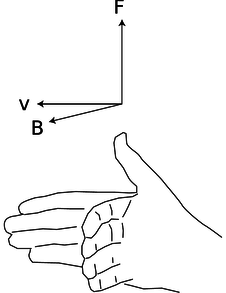
d / The right-hand relationship between the velocity of a positively charged particle, the magnetic field through which it is moving, and the magnetic force on it.
From this definition, we see that the magnetic field's units are N⋅s/C⋅m, which are usually abbreviated as teslas, 1 T=1 N⋅s/C⋅m. The definition implies a right-hand-rule relationship among the vectors, figure d, if the charge q is positive, and the opposite handedness if it is negative.

e / The unit of magnetic field, the tesla, is named after Serbian-American inventor Nikola Tesla.
This is not just a definition but a bold prediction! Is it really true that for any point in space, we can always find a vector B that successfully predicts the force on any passing particle, regardless of its charge and velocity vector? Yes --- it's not obvious that it can be done, but experiments verify that it can. How? Well for example, the cross product of parallel vectors is zero, so we can try particles moving in various directions, and hunt for the direction that produces zero force; the B vector lies along that line, in either the same direction the particle was moving, or the opposite one. We can then go back to our data from one of the other cases, where the force was nonzero, and use it to choose between these two directions and find the magnitude of the B vector. We could then verify that this vector gave correct force predictions in a variety of other cases.
Even with this empirical reassurance, the meaning of this equation is not intuitively transparent, nor is it practical in most cases to measure a magnetic field this way. For these reasons, let's look at an alternative method of defining the magnetic field which, although not as fundamental or mathematically simple, may be more appealing.
Definition in terms of the torque on a dipole
A compass needle in a magnetic field experiences a torque which tends to align it with the field. This is just like the behavior of an electric dipole in an electric field, so we consider the compass needle to be a magnetic dipole. In subsection 10.1.3 on page 567, we gave an alternative definition of the electric field in terms of the torque on an electric dipole.
To define the strength of a magnetic field, however, we need some way of defining the strength of a test dipole, i.e., we need a definition of the magnetic dipole moment. We could use an iron permanent magnet constructed according to certain specifications, but such an object is really an extremely complex system consisting of many iron atoms, only some of which are aligned with each other. A more fundamental standard dipole is a square current loop. This could be little resistive circuit consisting of a square of wire shorting across a battery, f.
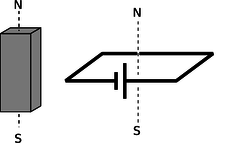
f / A standard dipole made from a square loop of wire shorting across a battery. It acts very much like a bar magnet, but its strength is more easily quantified.
Applying F=v×B, we find that such a loop, when placed in a magnetic field, g, experiences a torque that tends to align plane so that its interior “face” points in a certain direction.
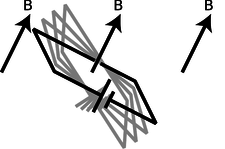
g / A dipole tends to align itself to the surrounding magnetic field.
Since the loop is symmetric, it doesn't care if we rotate it like a wheel without changing the plane in which it lies. It is this preferred facing direction that we will end up using as our alternative definition of the magnetic field.
If the loop is out of alignment with the field, the torque on it is proportional to the amount of current, and also to the interior area of the loop. The proportionality to current makes sense, since magnetic forces are interactions between moving charges, and current is a measure of the motion of charge. The proportionality to the loop's area is also not hard to understand, because increasing the length of the sides of the square increases both the amount of charge contained in this circular “river” and the amount of leverage supplied for making torque. Two separate physical reasons for a proportionality to length result in an overall proportionality to length squared, which is the same as the area of the loop. For these reasons, we define the magnetic dipole moment of a square current loop as
where the direction of the vectors is defined as shown in figure h.
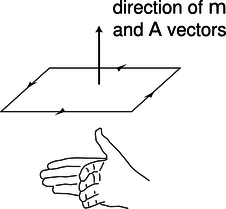
h / The m and A vectors.
We can now give an alternative definition of the magnetic field:
The magnetic field vector, B, at any location in space is defined by observing the torque exerted on a magnetic test dipole mt consisting of a square current loop. The field's magnitude is
where θ is the angle between the dipole vector and the field. This is equivalent to the vector cross product τ=mt×B.
Let's show that this is consistent with the previous definition, using the geometry shown in figure i.
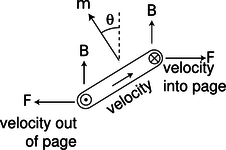
i / The torque on a current loop in a magnetic field. The current comes out of the page, goes across, goes back into the page, and then back across the other way in the hidden side of the loop.
The velocity vector that point in and out of the page are shown using the convention defined in figure j.

j / A vector coming out of the page is shown with the tip of an arrowhead. A vector going into the page is represented using the tailfeathers of the arrow.
Let the mobile charge carriers in the wire have linear density λ, and let the sides of the loop have length h, so that we have I=λv, and m=h2λv. The only nonvanishing torque comes from the forces on the left and right sides. The currents in these sides are perpendicular to the field, so the magnitude of the cross product F=qv×B is simply |F|=qvB. The torque supplied by each of these forces is r×F, where the lever arm r has length h/2, and makes an angle θ with respect to the force vector. The magnitude of the total torque acting on the loop is therefore
which is consistent with the second definition of the field.
It undoubtedly seems artificial to you that we have discussed dipoles only in the form of a square loop of current. A permanent magnet, for example, is made out of atomic dipoles, and atoms aren't square! However, it turns out that the shape doesn't matter. To see why this is so, consider the additive property of areas and dipole moments, shown in figure k.
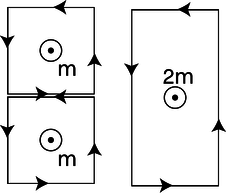
k / Dipole vectors can be added.
Each of the square dipoles has a dipole moment that points out of the page. When they are placed side by side, the currents in the adjoining sides cancel out, so they are equivalent to a single rectangular loop with twice the area. We can break down any irregular shape into little squares, as shown in figure l, so the dipole moment of any planar current loop can be calculated based on its area, regardless of its shape.
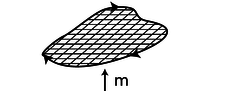
l / An irregular loop can be broken up into little squares.
| Example 1: The magnetic dipole moment of an atom |
|---|
| Let's make an order-of-magnitude estimate of the magnetic dipole moment of an atom. A hydrogen atom is about 10−10 m in diameter, and the electron moves at speeds of about 10−2c. We don't know the shape of the orbit, and indeed it turns out that according to the principles of quantum mechanics, the electron doesn't even have a well-defined orbit, but if we're brave, we can still estimate the dipole moment using the cross-sectional area of the atom, which will be on the order of (10−10 m)2=10−20 m2. The electron is a single particle, not a steady current, but again we throw caution to the winds, and estimate the current it creates as e/Δt, where Δt, the time for one orbit, can be estimated by dividing the size of the atom by the electron's velocity. (This is only a rough estimate, and we don't know the shape of the orbit, so it would be silly, for instance, to bother with multiplying the diameter by π based on our intuitive visualization of the electron as moving around the circumference of a circle.) The result for the dipole moment is m∼10−23 A⋅m2. Should we be impressed with how small this dipole moment is, or with how big it is, considering that it's being made by a single atom? Very large or very small numbers are never very interesting by themselves. To get a feeling for what they mean, we need to compare them to something else. An interesting comparison here is to think in terms of the total number of atoms in a typical object, which might be on the order of 1026 (Avogadro's number). Suppose we had this many atoms, with their moments all aligned. The total dipole moment would be on the order of 103 A⋅m2, which is a pretty big number. To get a dipole moment this strong using human-scale devices, we'd have to send a thousand amps of current through a one-square meter loop of wire! The insight to be gained here is that, even in a permanent magnet, we must not have all the atoms perfectly aligned, because that would cause more spectacular magnetic effects than we really observe. Apparently, nearly all the atoms in such a magnet are oriented randomly, and do not contribute to the magnet's dipole moment. |

m / The magnetic field pattern around a bar magnet is created by the superposition of the dipole fields of the individual iron atoms. Roughly speaking, it looks like the field of one big dipole, especially farther away from the magnet. Closer in, however, you can see a hint of the magnet's rectangular shape. The picture was made by placing iron filings on a piece of paper, and then bringing a magnet up underneath.
Discussion Questions
◊ The physical situation shown in figure c on page 648 was analyzed entirely in terms of forces. Now let's go back and think about it in terms of fields. The charge by itself up above the wire is like a test charge, being used to determine the magnetic and electric fields created by the wire. In figures c/1 and c/2, are there fields that are purely electric or purely magnetic? Are there fields that are a mixture of E and B? How does this compare with the forces?
◊ Continuing the analysis begun in discussion question A, can we come up with a scenario involving some charged particles such that the fields are purely magnetic in one frame of reference but a mixture of E and B in another frame? How about an example where the fields are purely electric in one frame, but mixed in another? Or an example where the fields are purely electric in one frame, but purely magnetic in another?
11.1.3 Some applications
| Example 2: Magnetic levitation |
|---|
|
n / Example 2.
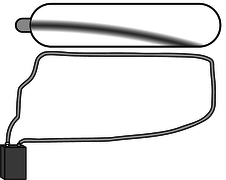
In figure n, a small, disk-shaped permanent magnet is stuck on the side of a battery, and a wire is clasped loosely around the battery, shorting it. A large current flows through the wire. The electrons moving through the wire feel a force from the magnetic field made by the permanent magnet, and this force levitates the wire. From the photo, it's possible to find the direction of the magnetic field made by the permanent magnet. The electrons in the copper wire are negatively charged, so they flow from the negative (flat) terminal of the battery to the positive terminal (the one with the bump, in front). As the electrons pass by the permanent magnet, we can imagine that they would experience a field either toward the magnet, or away from it, depending on which way the magnet was flipped when it was stuck onto the battery. By the right-hand rule (figure d on page 651), the field must be toward the battery. |
| Example 3: Nervous-system effects during an MRI scan<</th> |
|---|
| During an MRI scan of the head, the patient's nervous system is exposed to intense magnetic fields, and there are ions moving around in the nerves. The resulting forces on the ions can cause symptoms such as vertigo. |
| Example 4: A circular orbit |
|---|
| The magnetic force is always perpendicular to the motion of the particle, so it can never do any work, and a charged particle moving through a magnetic field does not experience any change in its kinetic energy: its velocity vector can change its direction, but not its magnitude. If the velocity vector is initially perpendicular to the field, then the curve of its motion will remain in the plane perpendicular to the field, so the magnitude of the magnetic force on it will stay the same. When an object experiences a force with constant magnitude, which is always perpendicular to the direction of its motion, the result is that it travels in a circle.
o / Magnetic forces cause a beam of electrons to move in a circle.
Figure o shows a beam of electrons in a spherical vacuum tube. In the top photo, the beam is emitted near the right side of the tube, and travels straight up. In the bottom photo, a magnetic field has been imposed by an electromagnet surrounding the vacuum tube; the ammeter on the right shows that the current through the electromagnet is now nonzero. We observe that the beam is bent into a circle. |
self-check:
Infer the direction of the magnetic field. Don't forget that the beam is made of electrons, which are negatively charged!
(answer in the back of the PDF version of the book)
Homework problem 12 is a quantitative analysis of circular orbits.
| Example 5: A velocity filter |
|---|
| Suppose you see the electron beam in figure o, and you want to determine how fast the electrons are going. You certainly can't do it with a stopwatch! Physicists may also encounter situations where they have a beam of unknown charged particles, and they don't even know their charges. This happened, for instance, when alpha and beta radiation were discovered. One solution to this problem relies on the fact that the force experienced by a charged particle in an electric field, FE=qE, is independent of its velocity, but the force due to a magnetic field, FB=qv×B, isn't. One can send a beam of charged particles through a space containing both an electric and a magnetic field, setting up the fields so that the two forces will cancel out perfectly for a certain velocity. Note that since both forces are proportional to the charge of the particles, the cancellation is independent of charge. Such a velocity filter can be used either to determine the velocity of an unknown beam or particles, or to select from a beam of particles only those having velocities within a certain desired range. Homework problem 7 is an analysis of this application. |
11.1.4 No magnetic monopoles
If you could play with a handful of electric dipoles and a handful of bar magnets, they would appear very similar. For instance, a pair of bar magnets wants to align themselves head-to-tail, and a pair of electric dipoles does the same thing. (It is unfortunately not that easy to make a permanent electric dipole that can be handled like this, since the charge tends to leak.)
You would eventually notice an important difference between the two types of objects, however. The electric dipoles can be broken apart to form isolated positive charges and negative charges. The two-ended device can be broken into parts that are not two-ended. But if you break a bar magnet in half, p, you will find that you have simply made two smaller two-ended objects.
p / You can't isolate the poles of a magnet by breaking it in half.
The reason for this behavior is not hard to divine from our microscopic picture of permanent iron magnets. An electric dipole has extra positive “stuff” concentrated in one end and extra negative in the other. The bar magnet, on the other hand, gets its magnetic properties not from an imbalance of magnetic “stuff” at the two ends but from the orientation of the rotation of its electrons. One end is the one from which we could look down the axis and see the electrons rotating clockwise, and the other is the one from which they would appear to go counterclockwise. There is no difference between the “stuff” in one end of the magnet and the other, q.
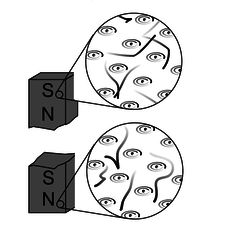
q / A magnetic dipole is made out of other dipoles, not out of monopoles.
Nobody has ever succeeded in isolating a single magnetic pole. In technical language, we say that magnetic monopoles not seem to exist. Electric monopoles do exist --- that's what charges are.
Electric and magnetic forces seem similar in many ways. Both act at a distance, both can be either attractive or repulsive, and both are intimately related to the property of matter called charge. (Recall that magnetism is an interaction between moving charges.) Physicists's aesthetic senses have been offended for a long time because this seeming symmetry is broken by the existence of electric monopoles and the absence of magnetic ones. Perhaps some exotic form of matter exists, composed of particles that are magnetic monopoles. If such particles could be found in cosmic rays or moon rocks, it would be evidence that the apparent asymmetry was only an asymmetry in the composition of the universe, not in the laws of physics. For these admittedly subjective reasons, there have been several searches for magnetic monopoles. Experiments have been performed, with negative results, to look for magnetic monopoles embedded in ordinary matter. Soviet physicists in the 1960's made exciting claims that they had created and detected magnetic monopoles in particle accelerators, but there was no success in attempts to reproduce the results there or at other accelerators. The most recent search for magnetic monopoles, done by reanalyzing data from the search for the top quark at Fermilab, turned up no candidates, which shows that either monopoles don't exist in nature or they are extremely massive and thus hard to create in accelerators.
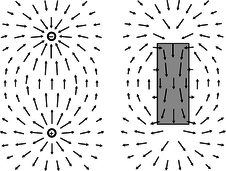
r / Magnetic fields have no sources or sinks.
The nonexistence of magnetic monopoles means that unlike an electric field, a magnetic one, can never have sources or sinks. The magnetic field vectors lead in paths that loop back on themselves, without ever converging or diverging at a point, as in the fields shown in figure r. Gauss' law for magnetism is therefore much simpler than Gauss' law for electric fields:
The magnetic flux through any closed surface is zero.
self-check:
Draw a Gaussian surface on the electric dipole field of figure r that has nonzero electric flux through it, and then draw a similar surface on the magnetic field pattern. What happens?
(answer in the back of the PDF version of the book)
| Example 6: The field of a wire |
|---|
| ▹ On page 650, we showed that a long, straight wire carrying current I exerts a magnetic force F=2kIqvc2R on a particle with charge q moving parallel to the wire with velocity v. What, then, is the magnetic field of the wire?
s / Example 6.
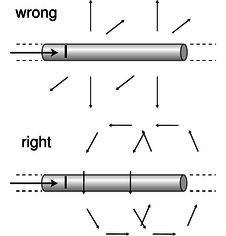
▹ Comparing the equation above to the first definition of the magnetic field, F=v×B, it appears that the magnetic field is one that falls off like 1/R, where R is the distance from the wire. However, it's not so easy to determine the direction of the field vector. There are two other axes along which the particle could have been moving, and the brute-force method would be to carry out relativistic calculations for these cases as well. Although this would probably be enough information to determine the field, we don't want to do that much work. Instead, let's consider what the possibilities are. The field can't be parallel to the wire, because a cross product vanishes when the two vectors are parallel, and yet we know from the case we analyzed that the force doesn't vanish when the particle is moving parallel to the wire. The other two possibilities that are consistent with the symmetry of the problem are shown in figure s. One is like a bottle brush, and the other is like a spool of thread. The bottle brush pattern, however, violates Gauss' law for magnetism. If we made a cylindrical Gaussian surface with its axis coinciding with the wire, the flux through it would not be zero. We therefore conclude that the spool-of-thread pattern is the correct one.4 Since the particle in our example was moving perpendicular to the field, we have |F|=|q||v||B|, so |B|=|F||q||v|=2kIc2R |
11.1.5 Symmetry and handedness
Imagine that you establish radio contact with an alien on another planet. Neither of you even knows where the other one's planet is, and you aren't able to establish any landmarks that you both recognize. You manage to learn quite a bit of each other's languages, but you're stumped when you try to establish the definitions of left and right (or, equivalently, clockwise and counterclockwise). Is there any way to do it?
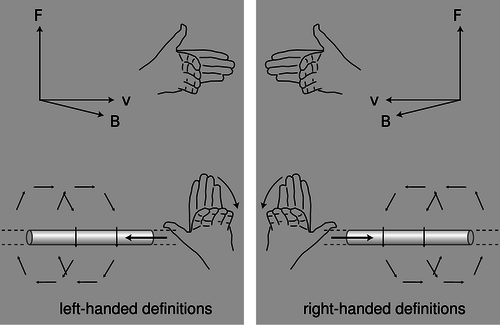
t / Left-handed and right-handed definitions.
If there was any way to do it without reference to external landmarks, then it would imply that the laws of physics themselves were asymmetric, which would be strange. Why should they distinguish left from right? The gravitational field pattern surrounding a star or planet looks the same in a mirror, and the same goes for electric fields. However, the magnetic field patterns shown in figure s seems to violate this principle. Could you use these patterns to explain left and right to the alien? No. If you look back at the definition of the magnetic field, it also contains a reference to handedness: the direction of the vector cross product. The aliens might have reversed their definition of the magnetic field, in which case their drawings of field patterns would look like mirror images of ours, as in the left panel of figure t.
Until the middle of the twentieth century, physicists assumed that any reasonable set of physical laws would have to have this kind of symmetry between left and right.

u / In this scene from Swan Lake, the the choreography has a symmetry with respect to left and right.
An asymmetry would be grotesque. Whatever their aesthetic feelings, they had to change their opinions about reality when experiments by C.S. Wu et al. showed that the weak nuclear force violates right-left symmetry!

v / C.S. Wu
It is still a mystery why right-left symmetry is observed so scrupulously in general, but is violated by one particular type of physical process.
Contributors
Benjamin Crowell (Fullerton College). Conceptual Physics is copyrighted with a CC-BY-SA license.