2.7: Spring Force- Hooke’s Law

Learning Objectives

• Describe the restoring force and displacement.
• Explain oscillatory motion under a spring force.

Figure \(\PageIndex{1}\): When displaced from its vertical equilibrium position, this plastic ruler oscillates back and forth because of the restoring force opposing displacement. When the ruler is on the left, there is a force to the right, and vice versa.

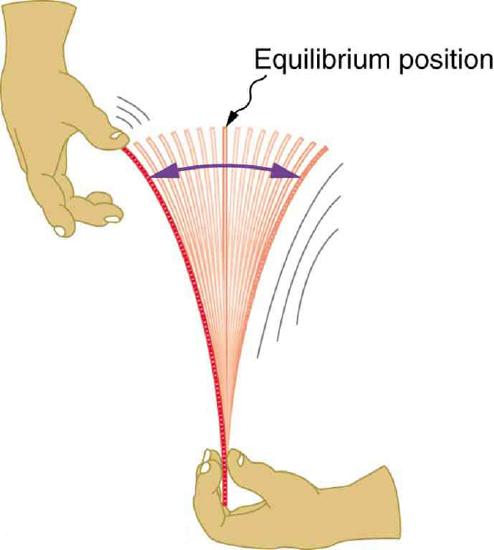
Newton’s first law implies that an object oscillating back and forth is experiencing forces. Without force, the object would move in a straight line at a constant speed rather than oscillate. Consider, for example, plucking a plastic ruler to the left as shown in Figure \(\PageIndex{1}\). The deformation of the ruler creates a force in the opposite direction, known as a restoring force. Once released, the restoring force causes the ruler to move back toward its stable equilibrium position, where the net force on it is zero. However, by the time the ruler gets there, it gains momentum and continues to move to the right, producing the opposite deformation. It is then forced to the left, back through equilibrium, and the process is repeated until dissipative forces dampen the motion. These forces remove mechanical energy from the system, gradually reducing the motion until the ruler comes to rest.

The simplest oscillations occur when the restoring force is directly proportional to displacement. This is called Hooke’s law force, or spring force:

\[F=-k x. \nonumber \]

Here, \(F\) is the restoring force, \(x\) is the displacement from equilibrium or deformation, and \(k\) is a constant related to the difficulty in deforming the system. The minus sign indicates the restoring force is in the direction opposite to the displacement.

Figure \(\PageIndex{2}\): (a) The plastic ruler has been released, and the restoring force is returning the ruler to its equilibrium position. (b) The net force is zero at the equilibrium position, but the ruler has momentum and continues to move to the right. (c) The restoring force is in the opposite direction. It stops the ruler and moves it back toward equilibrium again. (d) Now the ruler has momentum to the left. (e) In the absence of damping (caused by frictional forces), the ruler reaches its original position. From there, the motion will repeat itself.

The spring constant \(k\) is related to the rigidity (or stiffness) of a system—the larger the spring constant, the greater the restoring force, and the stiffer the system. The units of \(k\) are newtons per meter (N/m). Figure \(\PageIndex{3}\) shows a graph of the absolute value of the restoring force versus the displacement for a system that can be described by Hooke’s law—a simple spring in this case. The slope of the graph equals the spring constant \(k\) in newtons per meter.

Figure \(\PageIndex{3}\): (a) A graph of absolute value of the restoring force versus displacement is displayed. The fact that the graph is a straight line means that the system obeys Hooke’s law. The slope of the graph is the spring constant \(k\). (b) The data in the graph were generated by measuring the displacement of a spring from equilibrium while supporting various weights. The restoring force equals the weight supported, if the mass is stationary.

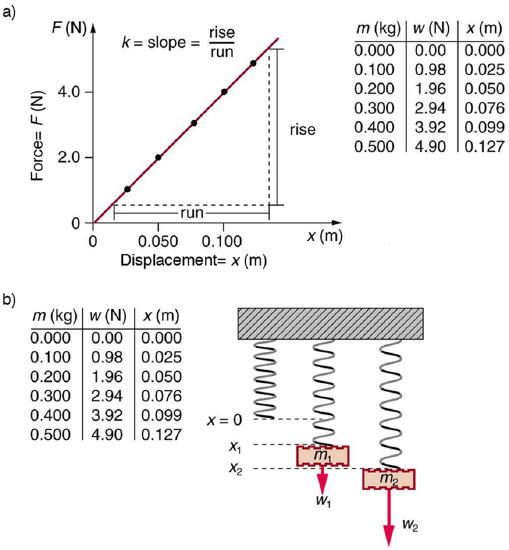
Example \(\PageIndex{1}\): How Stiff Are Car Springs?

Figure \(\PageIndex{4}\): The mass of a car increases due to the introduction of a passenger. This affects the displacement of the car on its suspension system. (credit: exfordy on Flickr)

What is the spring constant for the suspension system of a car that settles 1.20 cm when an 80.0-kg person gets in?

Strategy

Consider the car to be in its equilibrium position \(x=0\) before the person gets in. The car then settles down 1.20 cm, which means it is displaced to a position \(x=-1.20 \times 10^{-2} \mathrm{~m}\). At that point, the springs supply a restoring force \(F\) equal to the person’s weight \(w=m g=(80.0 \mathrm{~kg})\left(9.80 \mathrm{~m} / \mathrm{s}^{2}\right)=784 \mathrm{~N}\). We take this force to be \(F\) in Hooke’s law. Knowing \(F\) and \(x\), we can then solve the spring constant \(k\).

Solution

1. Solve Hooke’s law, \(F=-k x\), for \(k\):

   \[k=-\frac{F}{x}. \nonumber\]

   Substitute known values and solve \(k\):

   \[\begin{aligned}
   k &=-\frac{784 \mathrm{~N}}{-1.20 \times 10^{-2} \mathrm{~m}} \\
   &=6.53 \times 10^{4} \mathrm{~N} / \mathrm{m}.
   \end{aligned} \nonumber\]

Discussion

Note that \(F\) and \(x\) have opposite signs because they are in opposite directions—the restoring force is up, and the displacement is down. Also, note that the car would oscillate up and down when the person got in if it were not for damping (due to frictional forces) provided by shock absorbers. Bouncing cars are a sure sign of bad shock absorbers.

Section Summary

• An oscillation is a back and forth motion of an object between two points of deformation.
• An oscillation may create a wave, which is a disturbance that propagates from where it was created.
• The simplest type of oscillations and waves are related to systems that can be described by Hooke’s law:

  \[F=-k x, \nonumber\]

  where \(F\) is the restoring force, \(x\) is the displacement from equilibrium or deformation, and \(k\) is the spring constant of the system.

Glossary

deformation

displacement from equilibrium

spring constant

a constant related to the rigidity of a system: the larger the spring constant, the more rigid the system; the spring constant is represented by k

restoring force

force acting in opposition to the force caused by a deformation