4.6: Inelastic Collisions in One Dimension

Learning Objectives

• Define inelastic collision.
• Explain perfectly inelastic collision.
• Apply an understanding of collisions to everyday situations.
• Determine recoil velocity and loss in kinetic energy given mass and initial velocity.

We have seen that in an elastic collision, total kinetic energy is conserved. An inelastic collision is one in which the total kinetic energy changes (it is not conserved). This lack of conservation means that the forces between colliding objects may remove or add total kinetic energy. Work done by internal forces may change the forms of energy within a system. For inelastic collisions, such as when colliding objects stick together, this internal work may transform some kinetic energy into thermal energy. Or it may convert stored energy into total kinetic energy, such as when exploding bolts separate a satellite from its launch vehicle.

Definition: INELASTIC COLLISION

An inelastic collision is one in which the total kinetic energy changes (it is not conserved).

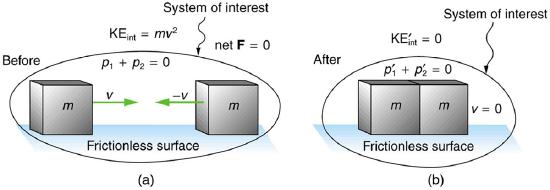
Figure \(\PageIndex{1}\) shows an example of an inelastic collision. Two objects that have equal masses head toward one another at equal speeds and then stick together. Their total kinetic energy is initially \(\frac{1}{2} m v^{2}+\frac{1}{2} m v^{2}=m v^{2}\). The two objects come to rest after sticking together, conserving total momentum. And the total kinetic energy is zero after this collision. A collision in which the objects stick together is called a perfectly inelastic collision because it reduces the total kinetic energy as much as possible, while conserving total momentum.

Definition: PERFECTLY INELASTIC COLLISION

A collision in which the objects stick together is sometimes called “perfectly inelastic.”

Figure \(\PageIndex{1}\): An inelastic one-dimensional two-object collision. Momentum is conserved, but total kinetic energy is not conserved. (a) Two objects of equal mass initially head directly toward one another at the same speed. (b) The objects stick together (a perfectly inelastic collision), and so their final velocity is zero.

Example \(\PageIndex{1}\): Calculating Velocity and Change in Kinetic Energy: Inelastic Collision of a Puck and a Goalie

(a) Find the recoil velocity of a 70.0-kg ice hockey goalie, originally at rest, who catches a 0.150-kg hockey puck slapped at him at a velocity of 35.0 m/s. (b) How much kinetic energy is lost during the collision? Assume friction between the ice and the puck-goalie system is negligible. (See Figure \(\PageIndex{2}\))

Figure \(\PageIndex{2}\): An ice hockey goalie catches a hockey puck and recoils backward. The initial kinetic energy of the puck is almost entirely converted to thermal energy and sound in this inelastic collision.

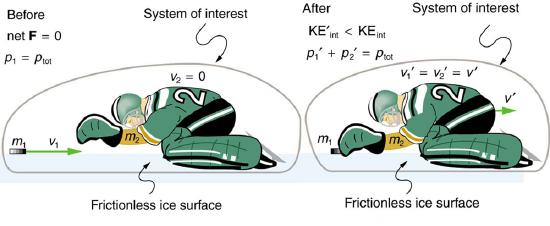
Strategy

Momentum is conserved because the net external force on the puck-goalie system is zero. We can thus use conservation of momentum to find the final velocity of the puck and goalie system. Note that the initial velocity of the goalie is zero and that the final velocity of the puck and goalie are the same. Once the final velocity is found, the kinetic energies can be calculated before and after the collision and compared as requested.

Solution for (a)

Momentum is conserved because the net external force on the puck-goalie system is zero.

Conservation of momentum is

\[p_{1}+p_{2}=p_{1}^{\prime}+p_{2}^{\prime} \nonumber\]

or

\[m_{1} v_{1}+m_{2} v_{2}=m_{1} v_{1}^{\prime}+m_{2} v_{2}^{\prime}. \nonumber\]

Because the goalie is initially at rest, we know \(v_{2}=0\). Because the goalie catches the puck, the final velocities are equal, or \(v_{1}^{\prime}=v_{2}^{\prime}=v^{\prime}\). Thus, the conservation of momentum equation simplifies to

\[m_{1} v_{1}=\left(m_{1}+m_{2}\right) v^{\prime}. \nonumber\]

Solving for \(v^{\prime}\) yields

\[v^{\prime}=\frac{m_{1}}{m_{1}+m_{2}} v_{1}. \nonumber\]

Entering known values in this equation, we get

\[v^{\prime}=\left(\frac{0.150 \mathrm{~kg}}{0.150 \mathrm{~kg}+70.0 \mathrm{~kg}}\right)(35.0 \mathrm{~m} / \mathrm{s})=7.48 \times 10^{-2} \mathrm{~m} / \mathrm{s}. \nonumber\]

Discussion for (a)

This recoil velocity is small and in the same direction as the puck’s original velocity, as we might expect.

Solution for (b)

Before the collision, the total kinetic energy \(\mathrm{KE}_{\text {int }}\) of the system is that of the hockey puck, because the goalie is initially at rest. Therefore, \(\mathrm{KE}_{\text {int }}\) is initially

\[\begin{aligned}
\mathrm{KE}_{\mathrm{int}} &=\frac{1}{2} m v^{2}=\frac{1}{2}(0.150 \mathrm{~kg})(35.0 \mathrm{~m} / \mathrm{s})^{2} \\
&=91.9 \mathrm{~J}
\end{aligned}. \nonumber\]

After the collision, the total kinetic energy is

\[\begin{aligned}
\mathrm{KE}_{\text {int }}^{\prime} &=\frac{1}{2}(m+M) v^{2}=\frac{1}{2}(70.15 \mathrm{~kg})\left(7.48 \times 10^{-2} \mathrm{~m} / \mathrm{s}\right)^{2} \\
&=0.196 \mathrm{~J}
\end{aligned}. \nonumber\]

The change in total kinetic energy is thus

\[\begin{aligned}
\mathrm{KE}_{\mathrm{int}}^{\prime}-\mathrm{KE}_{\mathrm{int}} &=0.196 \mathrm{~J}-91.9 \mathrm{~J} \\
&=-91.7 \mathrm{~J}
\end{aligned} \nonumber\]

where the minus sign indicates that the energy was lost.

Discussion for (b)

Nearly all of the initial total kinetic energy is lost in this perfectly inelastic collision. \(\mathrm{KE}_{\text {int }}\) is mostly converted to thermal energy and sound. Note that in this case, the total kinetic energy does not decrease all the way down to zero, because doing so would violate conservation of momentum, because initial total momentum is not zero. This is the most amount of energy that can be converted from the initial total kinetic energy without violating conservation of momentum.

Example \(\PageIndex{2}\): Calculating Final Velocity and Energy Release: Two Carts Collide

During some collisions stored energy may be converted into kinetic energy during a collision. Figure \(\PageIndex{3}\) shows a one-dimensional example in which two carts on an air track collide, releasing potential energy from a compressed spring.

Figure \(\PageIndex{3}\): An air track is nearly frictionless, so that momentum is conserved. Motion is one-dimensional. In this collision, examined in Example \(\PageIndex{2}\), the potential energy of a compressed spring is released during the collision and is converted to internal kinetic energy.

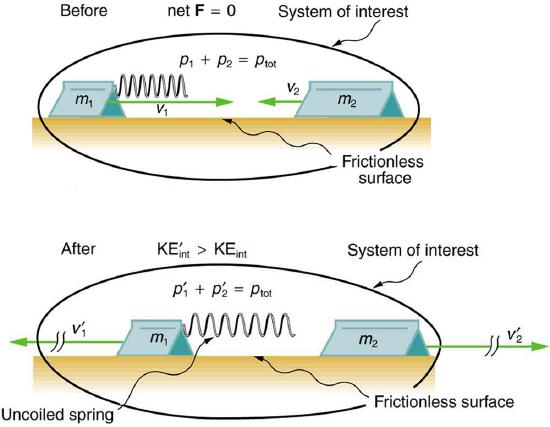
In the collision pictured in Figure \(\PageIndex{3}\), two carts collide inelastically. Cart 1 (denoted \(m_{1}\) carries a spring which is initially compressed. During the collision, the spring releases its potential energy and converts it to total kinetic energy. The mass of cart 1 and the spring is 0.350 kg, and the cart and the spring together have an initial velocity of \(2.00 \mathrm{~m} / \mathrm{s}\). Cart 2 (denoted \(m_{2}\) in Figure \(\PageIndex{3}\)) has a mass of 0.500 kg and an initial velocity of \(-0.500 \mathrm{~m} / \mathrm{s}\). After the collision, cart 1 is observed to recoil with a velocity of \(-4.00 \mathrm{~m} / \mathrm{s}\). (a) What is the final velocity of cart 2? (b) How much energy was released by the spring (assuming all of it was converted into internal kinetic energy)?

Strategy

We can use conservation of momentum to find the final velocity of cart 2, because \(F_{\text {net }}=0\) (the track is frictionless and the force of the spring is internal). Once this velocity is determined, we can compare the total kinetic energy before and after the collision to see how much energy was released by the spring.

Solution for (a)

As before, the equation for conservation of momentum in a two-object system is

\[m_{1} v_{1}+m_{2} v_{2}=m_{1} v_{1}^{\prime}+m_{2} v_{2}^{\prime}. \nonumber\]

The only unknown in this equation is \(v_{2}^{\prime}\). Solving for \(v_{2}^{\prime}\) and substituting known values into the previous equation yields

\[\begin{aligned}
v_{2}^{\prime} &=\frac{m_{1} v_{1}+m_{2} v_{2}-m_{1} v_{1}^{\prime}}{m_{2}} \\
&=\frac{(0.350 \mathrm{~kg})(2.00 \mathrm{~m} / \mathrm{s})+(0.500 \mathrm{~kg})(-0.500 \mathrm{~m} / \mathrm{s})}{0.500 \mathrm{~kg}}-\frac{(0.350 \mathrm{~kg})(-4.00 \mathrm{~m} / \mathrm{s})}{0.500 \mathrm{~kg}} \\
&=3.70 \mathrm{~m} / \mathrm{s}.
\end{aligned} \nonumber\]

Solution for (b)

The total kinetic energy before the collision is

\[\begin{aligned}
\mathrm{KE}_{\mathrm{int}} &=\frac{1}{2} m_{1} v_{1}^{2}+\frac{1}{2} m_{2} v_{2}^{2} \\
&=\frac{1}{2}(0.350 \mathrm{~kg})(2.00 \mathrm{~m} / \mathrm{s})^{2}+\frac{1}{2}(0.500 \mathrm{~kg})(-0.500 \mathrm{~m} / \mathrm{s})^{2} \\
&=0.763 \mathrm{~J}
\end{aligned}. \nonumber\]

After the collision, the total kinetic energy is

\[\begin{aligned}
\mathrm{KE}_{\text {int }}^{\prime} &=\frac{1}{2} m_{1} v_{1}^{\prime 2}+\frac{1}{2} m_{2} v_{2}^{\prime 2} \\
&=\frac{1}{2}(0.350 \mathrm{~kg})(-4.00 \mathrm{~m} / \mathrm{s})^{2}+\frac{1}{2}(0.500 \mathrm{~kg})(3.70 \mathrm{~m} / \mathrm{s})^{2} \\
&=6.22 \mathrm{~J}.
\end{aligned} \nonumber\]

The change in total kinetic energy is thus

\[\begin{aligned}
\mathrm{KE}_{\text {int }}^{\prime}-\mathrm{KE}_{\text {int }} &=6.22 \mathrm{~J}-0.763 \mathrm{~J} \\
&=5.46 \mathrm{~J}.
\end{aligned} \nonumber\]

Discussion

The final velocity of cart 2 is large and positive, meaning that it is moving to the right after the collision. The total kinetic energy in this collision increases by 5.46 J. That energy was released by the spring.

Section Summary

• An inelastic collision is one in which the total kinetic energy changes (it is not conserved).
• A collision in which the objects stick together is sometimes called perfectly inelastic because it reduces total kinetic energy as much as possible while conserving total momentum.

Glossary

inelastic collision

a collision in which total kinetic energy is not conserved

perfectly inelastic collision

a collision in which the colliding objects stick together