5.8: Angles of Reflection and Refraction
( \newcommand{\kernel}{\mathrm{null}\,}\)
Consider the situation shown in Figure 5.8.1:
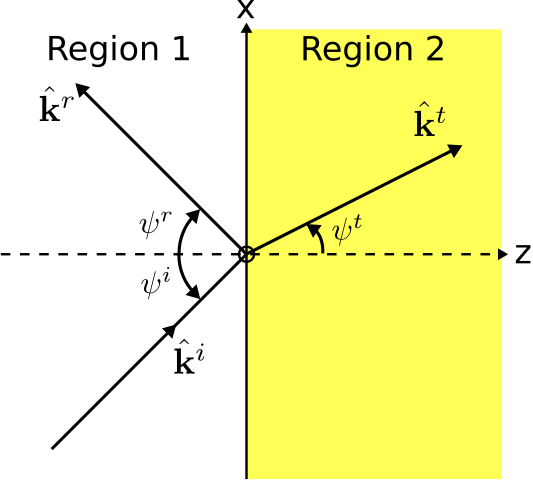 Figure 5.8.1: A uniform plane wave obliquely incident on the planar boundary between two semi-infinite material regions. ( CC BY-SA 4.0; C. Wang)
Figure 5.8.1: A uniform plane wave obliquely incident on the planar boundary between two semi-infinite material regions. ( CC BY-SA 4.0; C. Wang)
A uniform plane wave obliquely incident on the planar boundary between two semi-infinite material regions. Let a point on the boundary be represented as the position vector
r0=ˆxx+ˆyy
In both Sections 5.6 (“Plane Waves at Oblique Incidence on a Planar Boundary: TE Case”) and 5.7 (“Plane Waves at Oblique Incidence on a Planar Boundary: TM Case”), it is found that
ki⋅r0=kr⋅r0=kt⋅r0
In this expression,
ki=β1ˆkikr=β1ˆkrkt=β2ˆkt
where ˆki, ˆkr, and ˆkt are unit vectors in the direction of incidence, reflection, and transmission, respectively; and β1 and β2 are the phase propagation constants in Region 1 (from which the wave is incident) and Region 2, respectively. Equation ??? is essentially a boundary condition that enforces continuity of the phase of the electric and magnetic fields across the boundary, and is sometimes referred to as the “phase matching” requirement. Since the same requirement emerges independently in the TE and TM cases, and since any plane wave may be decomposed into TE and TM components, the requirement must apply to any incident plane wave regardless of polarization.
Equation ??? is the key to finding the direction of reflection ψr and direction of transmission ψt. First, observe:
ˆki=ˆxsinψi+ˆzcosψiˆkr=ˆxsinψr−ˆzcosψrˆkt=ˆxsinψt+ˆzcosψt
Therefore, we may express Equation ??? in the following form
β1(ˆxsinψi+ˆzcosψi)⋅(ˆxx+ˆyy)=β1(ˆxsinψr−ˆzcosψr)⋅(ˆxx+ˆyy)=β2(ˆxsinψt+ˆzcosψt)⋅(ˆxx+ˆyy)
which reduces to
β1sinψi=β1sinψr=β2sinψt
Examining the first and second terms of Equation ???, and noting that ψi and ψr are both limited to the range −π/2 to +π/2, we find that:
ψr=ψi
In plain English:
Angle of reflection equals angle of incidence.
Examining the first and third terms of Equation ???, we find that
β1sinψi=β2sinψt
Since β1=ω√μ1ϵ1 and β2=ω√μ2ϵ2, Equation ??? expressed explicitly in terms of the constitutive parameters is:
√μ1ϵ1sinψi=√μ2ϵ2sinψt
Thus, we see that ψt does not depend on frequency, except to the extent that the constitutive parameters might. We may also express this relationship in terms of the relative values of constitutive parameters; i.e., μ1=μr1μ0, ϵ1=ϵr1ϵ0, μ2=μr2μ0, and ϵ2=ϵr2ϵ0. In terms of the relative parameters:
√μr1ϵr1sinψi=√μr2ϵr2sinψt
This is known as Snell’s law or the law of refraction. Refraction is simply transmission with the result that the direction of propagation is changed.
Snell’s law (Equation ???) determines the angle of refraction (transmission).
The associated formula for ψt explicitly is:
ψt=arcsin(√μr1ϵr1μr2ϵr2sinψi)
For the common special case of non-magnetic media, one assumes μr1=μr2=1. In this case, Snell’s law simplifies to:
√ϵr1sinψi=√ϵr2sinψt
In optics, it is common to express permittivities in terms of indices of refraction; e.g., n1≜√ϵr1 and n2≜√ϵr2. Thus, Snell’s law in optics is often expressed as:
n1sinψi=n2sinψt
When both media are non-magnetic, Equation ??? simplifies to
ψt=arcsin(√ϵr1ϵr2sinψi)
When ϵr2>ϵr1, we observe that ψt<ψi. In other words, the transmitted wave travels in a direction that is closer to the surface normal than the angle of incidence. This scenario is demonstrated in the following example.
Figure 5.8.2 shows a narrow beam of light that is incident from air to glass at an angle ψi=60∘.
 Figure 5.8.2: Angles of reflection and refraction for a light wave incident from air onto glass. (CC BY-SA 3.0; Z. Sándor)
Figure 5.8.2: Angles of reflection and refraction for a light wave incident from air onto glass. (CC BY-SA 3.0; Z. Sándor)
As expected, the angle of reflection ψr is observed to be equal to ψi. The angle of refraction ψt is observed to be 35∘. What is the relative permittivity of the glass?
Solution
Since the permittivity of glass is greater than that of air, we observe the expected result ψt<ψi. Since glass is non-magnetic, the expected relationship between these angles is given by Equation ???. Solving that equation for the relative permittivity of the glass, we obtain:
ϵr2=ϵr1(sinψisinψt)2≅2.28_
When a wave travels in the reverse direction – i.e., from a non-magnetic medium of higher permittivity to a medium of lower permittivity – one finds ψt>ψr. In other words, the refraction is away from the surface normal. Figure 5.8.3 shows an example from common experience.
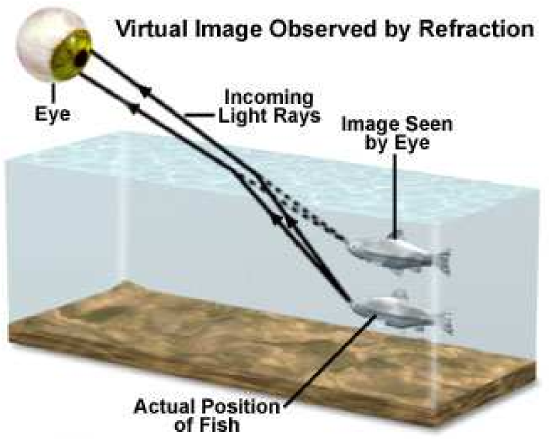 Figure 5.8.3: Refraction accounts for the apparent displacement of an underwater object from the perspective of an observer above the water. (CC BY-SA 4.0; G. Saini)
Figure 5.8.3: Refraction accounts for the apparent displacement of an underwater object from the perspective of an observer above the water. (CC BY-SA 4.0; G. Saini)
In non-magnetic media, when ϵr1<ϵr2, ψt<ψi (refraction toward the surface normal). When ϵr1>ϵr2, ψt>ψi (refraction away from the surface normal).
Under certain conditions, the ϵr2<ϵr1 case leads to the following surprising observation: When calculating ψt using, for example, Equation ???, one finds that √ϵr1/ϵr2sinψi can be greater than 1. Since the sin function yields values between −1 and +1, the result of the arcsin function is undefined. This odd situation is addressed in Section 5.11. For now, we will simply note that this condition leads to the phenomenon of total internal reflection. For now, all we can say is that when ϵr2<ϵr1, ψt is able to reach π/2 radians, which corresponds to propagation parallel to the boundary. Beyond that threshold, we must account for the unique physical considerations associated with total internal reflection.
We conclude this section with a description of the common waveguiding device known as the prism, shown in Figure 5.8.4. This particular device uses refraction to change the direction of light waves (similar devices can be used to manipulate radio waves as well).
 Figure 5.8.4: A typical triangular prism ( CC BY-SA 3.0; D-Kuru)
Figure 5.8.4: A typical triangular prism ( CC BY-SA 3.0; D-Kuru)
Many readers are familiar with the use of prisms to separate white light into its constituent colors (frequencies), as shown in Figure 5.8.5. The separation of colors is due to frequency dependence of the material comprising the prism. Specifically, the permittivity of the material is a function of frequency, and therefore the angle of refraction is a function of frequency. Thus, each frequency is refracted by a different amount. Conversely, a prism comprised of a material whose permittivity exhibits negligible variation with frequency will not separate incident white light into its constituent colors since each color will be refracted by the same amount.
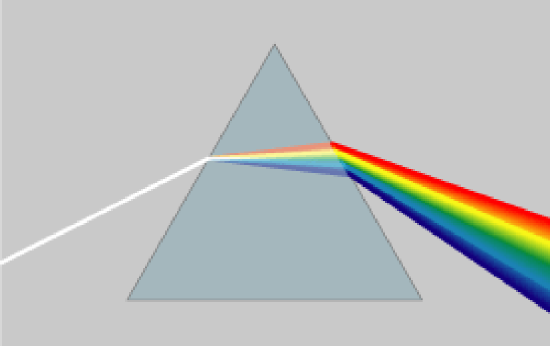 Figure 5.8.5: A color-separating prism. ( CC BY-SA 4.0; Suidroot)
Figure 5.8.5: A color-separating prism. ( CC BY-SA 4.0; Suidroot)


