1.6D: Field on the Axis of and in the Plane of a Charged Ring
- Page ID
- 6475
Field on the axis of a charged ring.
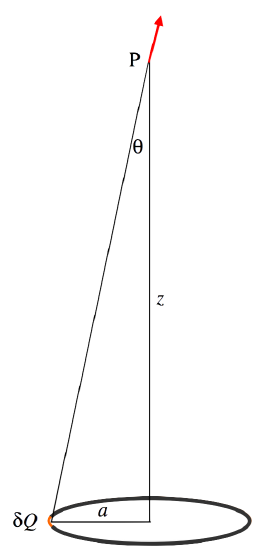
Ring, radius \(a\), charge \(Q\). Field at P from element of charge \(δQ = \dfrac{\delta Q}{4\pi\epsilon_0 (a^2+z^2)}\). Vertical component of this \(= \dfrac{\delta Q \cos \theta}{4\pi\epsilon_0 (a^2+z^2)}=\dfrac{\delta Qz}{4\pi\epsilon_0 (a^2+z^2)^{3/2}}\). Integrate for entire ring:
Field \(E = \dfrac{Q}{4\pi\epsilon_0}\dfrac{z}{(a^2+z^2)^{3/2}}\).
In terms of dimensionless variables:
\[E=\dfrac{z}{(1+z^2)^{3/2}}.\]
where E is in units of \(\dfrac{Q}{4\pi\epsilon_0 a^2}\), and \(z\) is in units of \(a\).
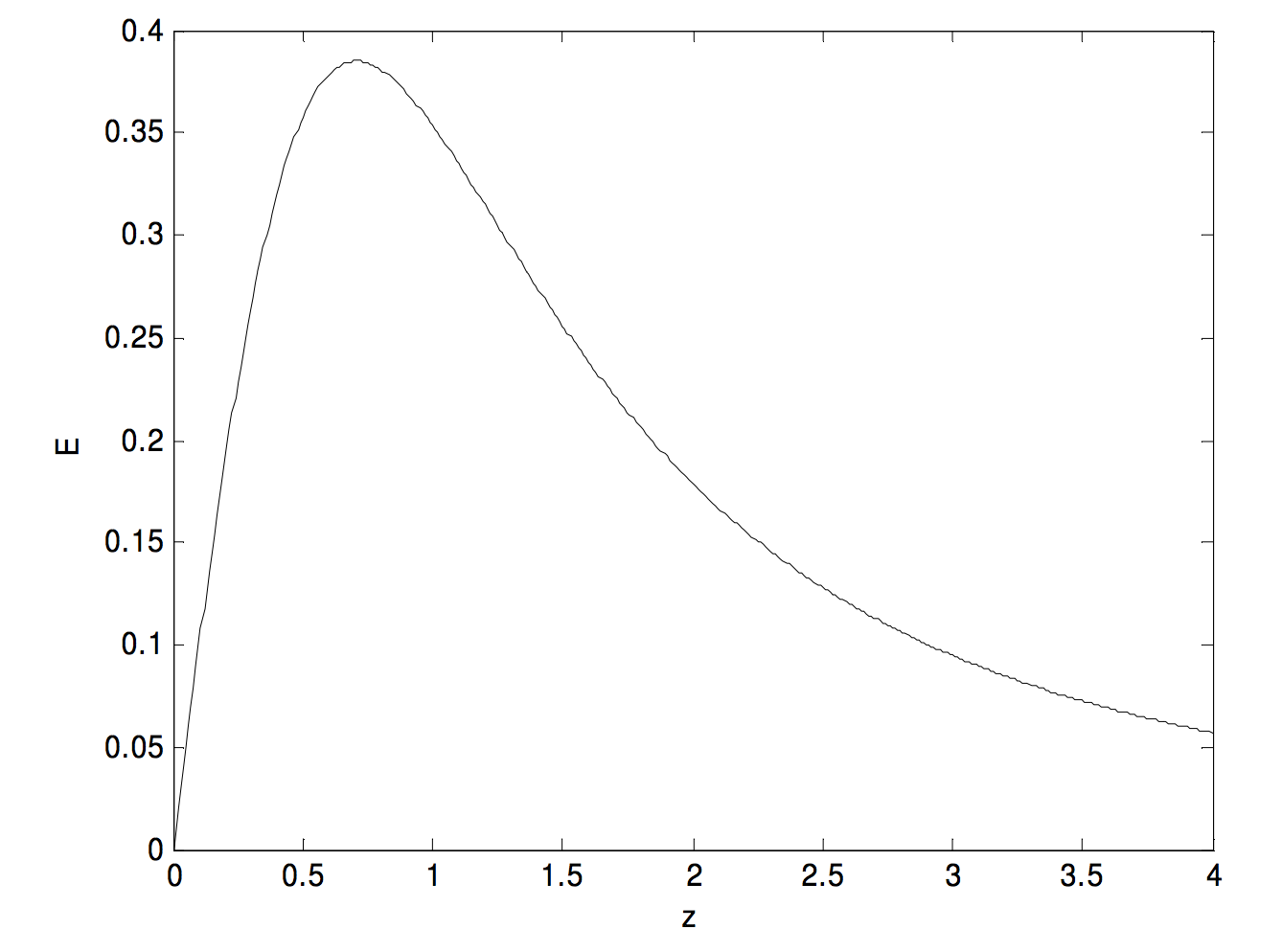
From calculus, we find that this reaches a maximum value of \(\dfrac{2\sqrt{3}}{9}=0.3849\) at \(z=1/\sqrt{2}=0.7071\).
It reaches half of its maximum value where \(\dfrac{z}{(1+z^2)^{3/2}}=\dfrac{\sqrt{3}}{9}\).
That is, \(3-72Z+9Z^2+3Z^2=0\), where \(Z=z^2\).
The two positive solution are \(Z = 0.041889 \text{ and }3.596267\).
That is, \(z = 0.2047 \text{ and }1.8964\).
Field in the plane of a charged ring.
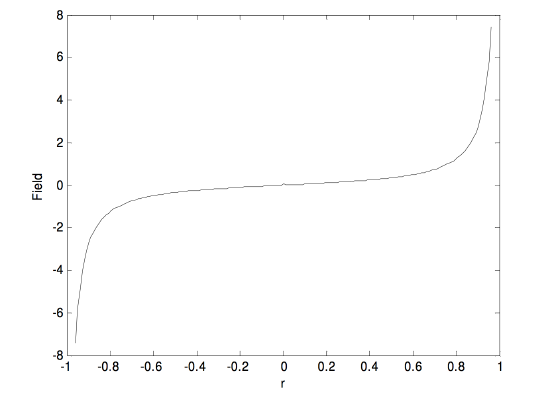
We suppose that we have a ring of radius \(a\) bearing a charge \(Q\). We shall try to find the field at a point in the plane of the ring and at a distance \(r (0 ≤ r < a)\) from the centre of the ring.
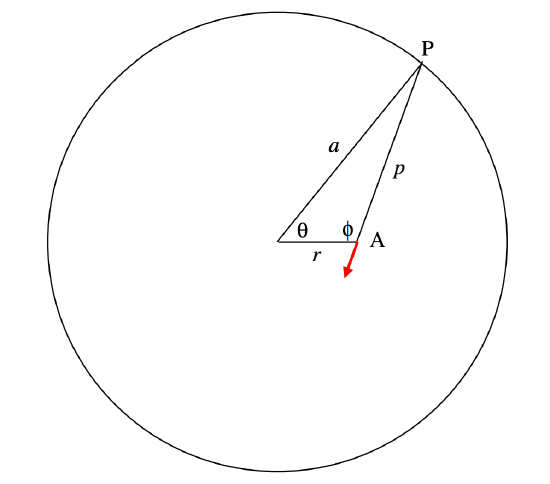
Consider an element \(δθ\) of the ring at P. The charge on it is \(\dfrac{Q\delta \theta}{2\pi}\). The field at A from this element of charge is
\[\dfrac{1}{4\pi\epsilon_0}\cdot \dfrac{Q\delta\theta}{2\pi}\cdot \dfrac{1}{a^2+r^2-2ar\cos \theta}=\dfrac{Q}{4\pi\epsilon_0 .2\pi a^2}\cdot \dfrac{\delta\theta}{b-c\cos \theta},\]
where \(b=1+r^2/a^2\) and \(c = 2r / a\). The component of this toward the centre is
\(-\dfrac{Q}{4\pi\epsilon_0 .2 \pi a^2}\cdot\dfrac{\cos \phi \delta\theta}{b-c\cos \theta}\).
To find the field at A due to the entire ring, we must express \(\phi\) in terms of \(θ\), \(r \) and \(a\), and integrate with respect to \(θ \text{ from }0 \text{ to }2π\) (or from \(0 \text{ to }π\) and double it). The necessary relations are
\[p^2=a^2+r^2-2ar\cos \theta\]
\[\cos \phi = \dfrac{r^2+p^2-a^2}{2rp}.\]
The result of the numerical integration is shown below, in which the field is expressed in units of \(Q/(4\pi\epsilon_0 a^2)\) and \(r\) is in units of \(a\).