1.6C: A Long, Charged Rod

A long rod bears a charge of $λ$ coulombs per metre of its length. What is the strength of the electric field at a point P at a distance $r$ from the rod?

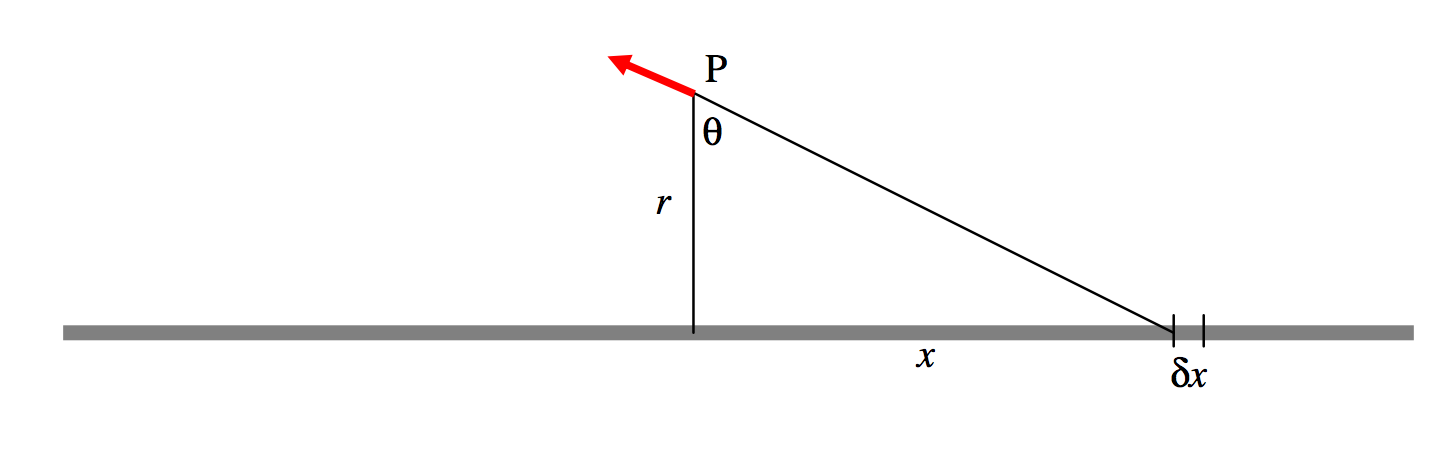
$\text{FIGURE I.2}$

Consider an element $δx$ of the rod at a distance $(r^2 + x^2 )^{1/2}$ from the rod. It bears a charge $λ$ $δx$. The contribution to the electric field at P from this element is $\frac{1}{4\pi\epsilon_0}\cdot \frac{\lambda \delta x}{r^2 + x^2}$ in the direction shown. The radial component of this is $\frac{1}{4\pi\epsilon_0}\cdot \frac{\lambda \delta x}{r^2 +x^2}\cos θ$. But $x=r\tan \theta,\, \delta x=r\sec^2 \theta \,\delta \theta \text{ and }r^2+x^2 = r^2\sec^2 \theta$. Therefore the radial component of the field from the element $δx$ is $\frac{\lambda}{4\pi\epsilon_0 r}\cos \theta \, \delta \theta$. To find the radial component of the field from the entire rod, we integrate along the length of the rod. If the rod is infinitely long (or if its length is much greater than r), we integrate from $θ = −π/2 \text{ to }+ π/2$, or, what amounts to the same thing, from $0 \text{ to }π/2$, and double it. Thus the radial component of the field is

$$\tag{1.6.8} E=\frac{2\lambda}{4\pi\epsilon_0 r}\int_0^{\pi/2}\cos \theta \, \delta \theta = \frac{\lambda}{2\pi\epsilon_0 r}.$$

The component of the field parallel to the rod, by considerations of symmetry, is zero, so Equation 1.6.8 gives the total field at a distance $r$ from the rod, and it is directed radially away from the rod.

Notice that Equation 1.6.4 for a spherical charge distribution has $4πr^2$ in the denominator, while Equation 1.6.8, dealing with a problem of cylindrical symmetry, has $2πr$.