1.6E: Field on the Axis of a Uniformly Charged Disc
( \newcommand{\kernel}{\mathrm{null}\,}\)
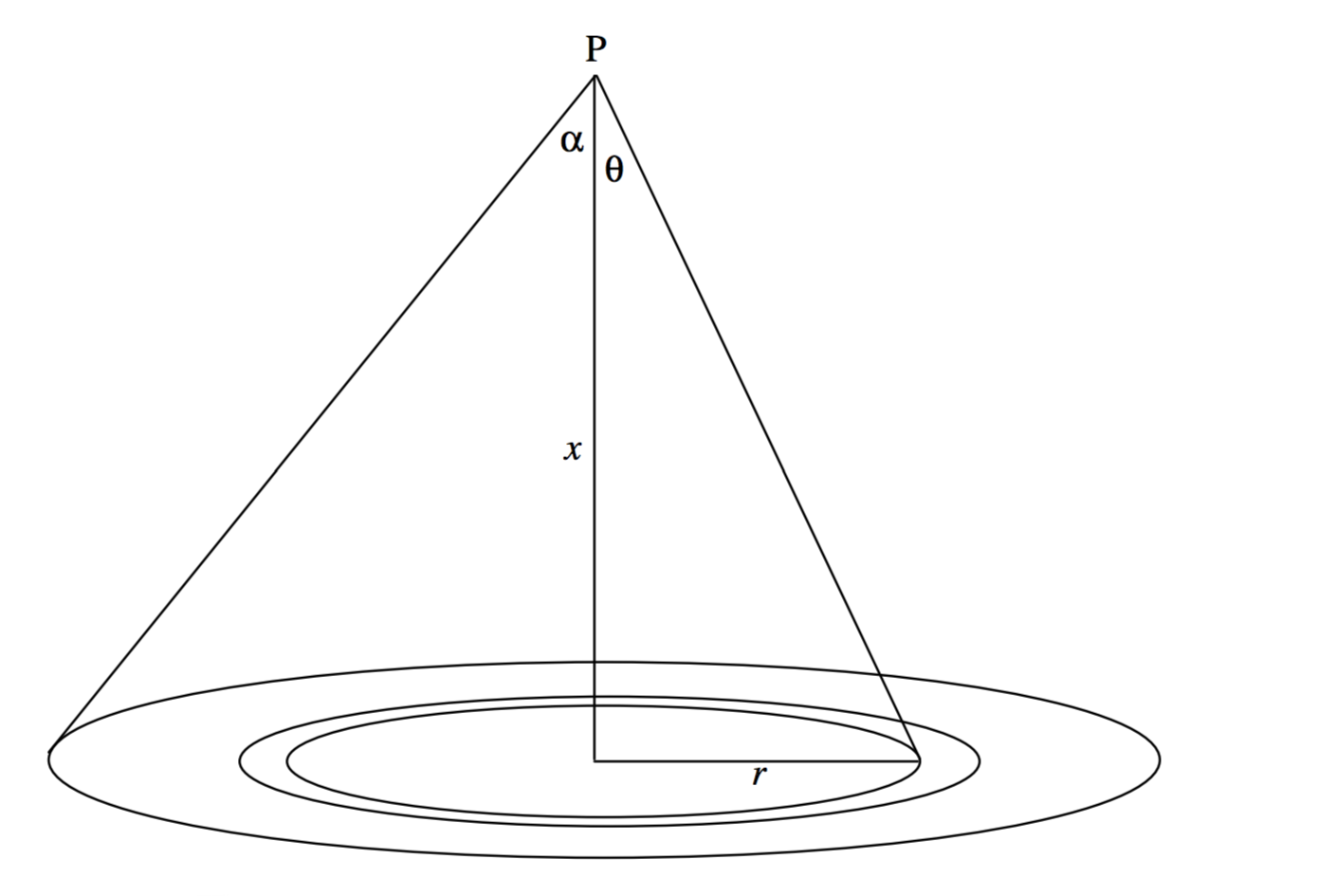
\text{FIGURE I.3}
We suppose that we have a circular disc of radius a bearing a surface charge density of σ coulombs per square metre, so that the total charge is Q = πa^2 σ. We wish to calculate the field strength at a point P on the axis of the disc, at a distance x from the centre of the disc.
Consider an elemental annulus of the disc, of radii r and r + δr. Its area is 2πrδr and so it carries a charge 2πσrδr. Using the result of subsection 1.6.4, we see that the field at P from this charge is
\frac{2\pi\sigma r \,\delta r}{4\pi\epsilon_0}\cdot \frac{x}{(r^2+x^2)^{3/2}}=\frac{\sigma x}{2\epsilon_0}\cdot \frac{r\,\delta r}{(r^2+x^2)^{3/2}}.
But r=x\tan \theta,\, \delta r=x\sec^2 \theta \delta \theta \text{ and }(r^2+x^2)^{1/2}=x\sec \theta. Thus the field from the elemental annulus can be written
\frac{\sigma}{2\epsilon_0}\sin \theta \,\delta \theta .
The field from the entire disc is found by integrating this from θ = 0 \text{ to }θ = α to obtain
E=\frac{\sigma}{2\epsilon_0}(1-\cos α )=\frac{\sigma}{2\epsilon_0}\left ( 1-\frac{x}{(a^2+x^2)^{1/2}}\right ).\tag{1.6.11}
This falls off monotonically from σ/(2\epsilon_0) just above the disc to zero at infinity.


