5.10: Energy Stored in a Capacitor
- Page ID
- 6018
Let us imagine (Figure \(V.\)10) that we have a capacitor of capacitance \(C\) which, at some time, has a charge of \(+q\) on one plate and a charge of \(-q\) on the other plate. The potential difference across the plates is then \(q/C\). Let us now take a charge of \(+\delta q\) from the bottom plate (the negative one) and move it up to the top plate. We evidently have to do work to do this, in the amount of \(\frac{q}{C}\delta q\).
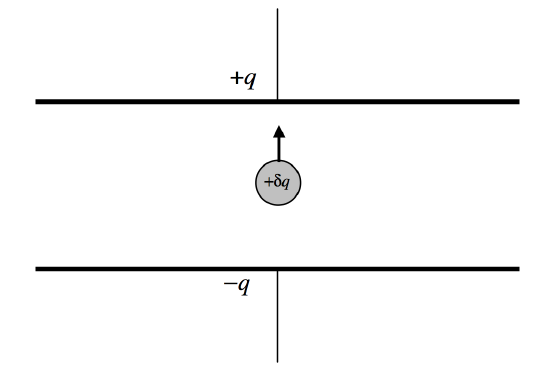
\(\text{FIGURE V.10}\)
The total work required, then, starting with the plates completely uncharged until we have transferred a charge \(Q\) from one plate to the other is
\[\frac{1}{C}\int_0^Q q\,dq=Q^2/(2C)\label{5.10.1}\tag{5.10.1}\]
This is, then, the energy \(U\) stored in the capacitor, and, by application of \(Q = CV \) it can also be written \(U=\frac{1}{2}QV\), or, more usually,
\[U=\frac{1}{2}CV^2\label{5.10.2}\tag{5.10.2}\]
Verify that this has the correct dimensions for energy. Also, think about how many expressions for energy you know that are of the form \(\frac{1}{2}ab^2\). There are more to come.


