5.10: Energy Stored in a Capacitor

Let us imagine (Figure $V.$10) that we have a capacitor of capacitance $C$ which, at some time, has a charge of $+q$ on one plate and a charge of $-q$ on the other plate. The potential difference across the plates is then $q/C$. Let us now take a charge of $+\delta q$ from the bottom plate (the negative one) and move it up to the top plate. We evidently have to do work to do this, in the amount of $\frac{q}{C}\delta q$.

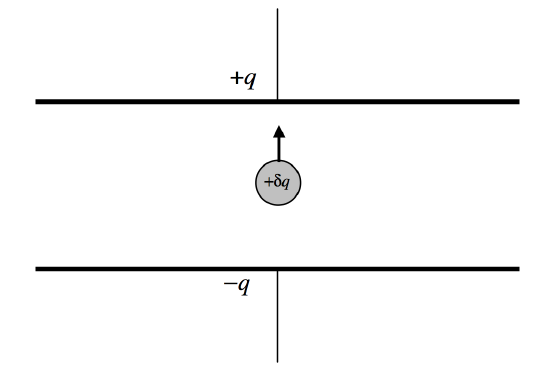
$\text{FIGURE V.10}$

The total work required, then, starting with the plates completely uncharged until we have transferred a charge $Q$ from one plate to the other is

$$\frac{1}{C}\int_0^Q q\,dq=Q^2/(2C)\label{5.10.1}\tag{5.10.1}$$

This is, then, the energy $U$ stored in the capacitor, and, by application of $Q = CV$ it can also be written $U=\frac{1}{2}QV$, or, more usually,

$$U=\frac{1}{2}CV^2\label{5.10.2}\tag{5.10.2}$$

Verify that this has the correct dimensions for energy. Also, think about how many expressions for energy you know that are of the form $\frac{1}{2}ab^2$. There are more to come.