6.5: Magnetic Field Near a Long, Straight, Current-carrying Conductor

Consider a point $P$ at a distance $a$ from a conductor carrying a current $I$ (Figure VI.4).

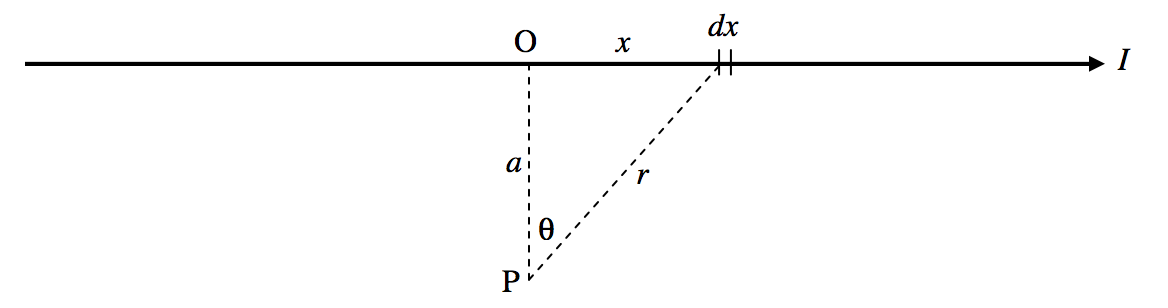
$\text{FIGURE VI.4}$

The contribution to the magnetic field at $P$ from the elemental length $dx$ is

$$dB = \frac{\mu}{4\pi}\cdot \frac{I\,dx \cos \theta }{r^2}.\label{6.5.1}$$

(Look at the way I have drawn $\theta$ if you are worried about the cosine.)

Here I have omitted the subscript zero on the permeability to allow for the possibility that the wire is immersed in a medium in which the permeability is not the same as that of a vacuum. (The permeability of liquid oxygen, for example, is slightly greater than that of free space.) The direction of the field at $P$ is into the plane of the “paper” (or of your computer screen).

We need to express this in terms of one variable, and we’ll choose $\theta$. We can see that $r=a\sec \theta$ and $x=a\tan \theta$ so that $dx=a\sec^2 \theta \, d\theta$. Thus Equation $\ref{6.5.1}$ becomes

$$dB=\frac{\mu I}{4\pi a}\sin \theta \, d\theta .$$

Upon integrating this from $-\pi/2 \text{ to }+ \pi/2$ (or from $0\text{ to }\pi/2$ and then double it), we find that the field at $P$ is

$$B=\frac{\mu I}{2\pi a}.$$

Note the $2\pi$ in this problem with cylindrical symmetry.