5.1: Introduction
- Page ID
- 5438
A capacitor consists of two metal plates separated by a nonconducting medium (known as the dielectric medium or simply the dielectric) or by a vacuum. It is represented by the electrical symbol
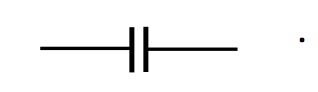
Capacitors of one sort or another are included in almost any electronic device. Physically, there is a vast variety of shapes, sizes and construction, depending upon their particular application. This chapter, however, is not primarily concerned with real, practical capacitors and how they are made and what they are used for, although a brief section at the end of the chapter will discuss this. In addition to their practical uses in electronic circuits, capacitors are very useful to professors for torturing students during exams, and, more importantly, for helping students to understand the concepts of and the relationships between electric fields \(\textbf{E} \text{ and }\textbf{D}\), potential difference, permittivity, energy, and so on. The capacitors in this chapter are, for the most part, imaginary academic concepts useful largely for pedagogical purposes. Need the electronics technician or electronics engineer spend time on these academic capacitors, apparently so far removed from the real devices to be found in electronic equipment? The answer is surely and decidedly yes – more than anyone else, the practical technician or engineer must thoroughly understand the basic concepts of electricity before even starting with real electronic devices.
If a potential difference is maintained across the two plates of a capacitor (for example, by connecting the plates across the poles of a battery) a charge +\(Q\) will be stored on one plate and -\(Q\) on the other. The ratio of the charge stored on the plates to the potential difference \(V\) across them is called the capacitance \(C\) of the capacitor. Thus:
\[Q=CV.\label{5.1.1}\]
If, when the potential difference is one volt, the charge stored is one coulomb, the capacitance is one farad, F. Thus, a farad is a coulomb per volt. It should be mentioned here that, in practical terms, a farad is a very large unit of capacitance, and most capacitors have capacitances of the order of microfarads, \(\mu\)F.
The dimensions of capacitance are \(\frac{Q}{\text{ML}^2\text{T}^{-2}\text{Q}^{-1}}=\text{M}^{-1}\text{L}^{-2}\text{T}^2\text{Q}^2\).
It might be remarked that, in older books, a capacitor was called a “condenser”, and its capacitance was called its “capacity”. Thus what we would now call the “capacitance of a capacitor” was formerly called the “capacity of a condenser”.
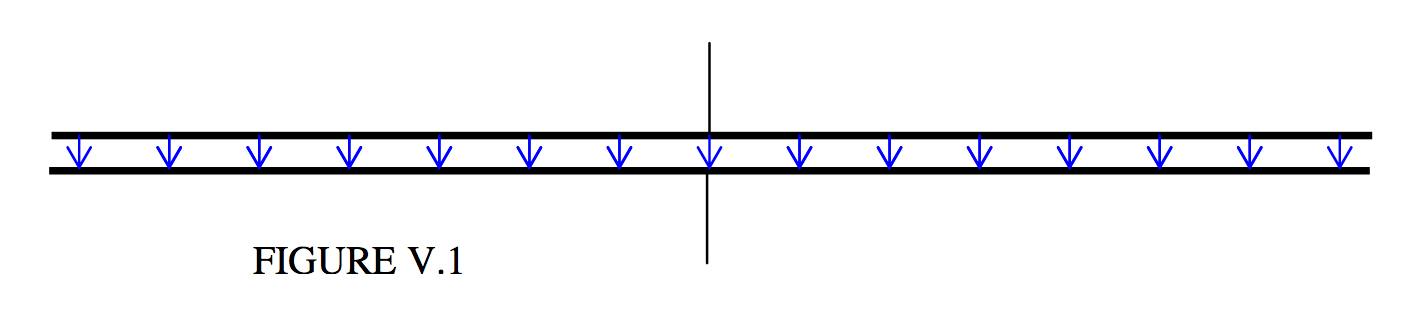
In the highly idealized capacitors of this chapter, the linear dimensions of the plates (length and breadth, or diameter) are supposed to be very much larger than the separation between them. This in fact is nearly always the case in real capacitors, too, though perhaps not necessarily for the same reason. In real capacitors, the distance between the plates is small so that the capacitance is as large as possible. In the imaginary capacitors of this chapter, I want the separation to be small so that the electric field between the plates is uniform. Thus the capacitors I shall be discussing are mostly like Figure \(V.\)1, where I have indicated, in blue, the electric field between the plates:
However, I shall not always draw them like this, because it is rather difficult to see what is going on inside the capacitor. I shall usually much exaggerate the scale in one direction, so that my drawings will look more like this:
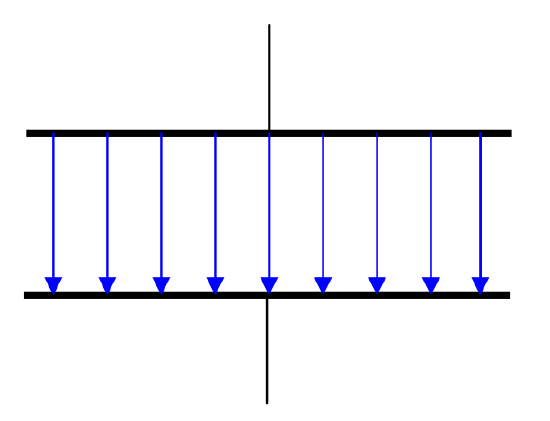
\(\text{FIGURE V.2}\)
If the separation were really as large as this, the field would not be nearly as uniform as indicated; the electric field lines would greatly bulge outwards near the edges of the plates.
In the next few sections we are going to derive formulas for the capacitances of various capacitors of simple geometric shapes.


