3.2: Poynting Vector
( \newcommand{\kernel}{\mathrm{null}\,}\)
In this section, we use Poynting’s theorem (Section 3.1) to confirm the interpretation of the Poynting vector
S≜E×H
as the spatial power density (SI base units of W/m2) and the direction of power flow.
Figure 3.2.1 shows a uniform plane wave incident on a homogeneous and lossless region V defined by the closed right cylinder S. The axis of the cylinder is aligned along the direction of propagation ˆk of the plane wave. The ends of the cylinder are planar and perpendicular to ˆk.
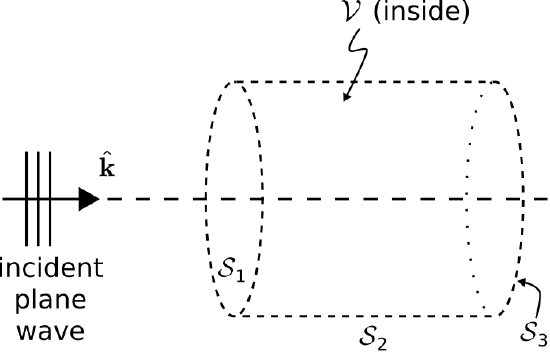 Figure 3.2.1: A uniform plane wave incident on a region bounded by the cylindrical surface S. ( CC BY-SA 4.0; C. Wang)
Figure 3.2.1: A uniform plane wave incident on a region bounded by the cylindrical surface S. ( CC BY-SA 4.0; C. Wang)
Now let us apply Poynting’s theorem:
Pnet,in=PΩ+∂∂tWe+∂∂tWm
Since the region is lossless, PΩ=0. Presuming no other electric or magnetic fields, We and Wm must also be zero. Consequently, Pnet,in=0. However, this does not mean that there is no power flowing into V. Instead, Pnet,in=0 merely indicates that the net power flowing into V is zero. Thus, we might instead express the result for the present scenario as follows:
Pnet,in=Pin−Pout=0
where Pin and Pout indicate power flow explicitly into and explicitly out of V as separate quantities.
Proceeding, let’s ignore what we know about power flow in plane waves, and instead see where Poynting’s theorem takes us. Here,
Pnet,in≜−∮S(E×H)⋅ds=0
The surface S consists of three sides: The two flat ends, and the curved surface that connects them. Let us refer to these sides as S1, S2, and S3, from left to right as shown in Figure 3.2.1. Then,
−∫S1(E×H)⋅ds−∫S2(E×H)⋅ds−∫S3(E×H)⋅ds=0
On the curved surface S2, ds is everywhere perpendicular to E×H (i.e., perpendicular to ˆk). Therefore, the second integral is equal to zero. On the left end S1, the outward-facing differential surface element ds=−ˆkds. On the right end S3, ds=+ˆkds. We are left with:
∫S1(E×H)⋅ˆkds−∫S3(E×H)⋅ˆkds=0
Compare this to Equation ???. Since ˆk is, by definition, the direction in which E×H points, the first integral must be Pin and the second integral must be Pout. Thus,
Pin=∫S1(E×H)⋅ˆkds
and it follows that the magnitude and direction of E×H, which we recognize as the Poynting vector, are spatial power density and direction of power flow, respectively.
The Poynting vector is named after English physicist J.H. Poynting, one of the co-discoverers of the concept. The fact that this vector points in the direction of power flow, and is therefore also a “pointing vector,” is simply a remarkable coincidence.
Additional Reading:
- “Poynting vector” on Wikipedia.


