3.4: Complex Permittivity
( \newcommand{\kernel}{\mathrm{null}\,}\)
The relationship between electric field intensity {\bf E} (SI base units of V/m) and electric flux density {\bf D} (SI base units of C/m^2) is:
{\bf D} = \epsilon{\bf E} \label{m0134_eD}
where \epsilon is the permittivity (SI base units of F/m). In simple media, \epsilon is a real positive value which does not depend on the time variation of {\bf E}. That is, the response ({\bf D}) to a change in {\bf E} is observed instantaneously and without delay.
In practical materials, however, the change in {\bf D} in response to a change in {\bf E} may depend on the manner in which {\bf E} changes. The response may not be instantaneous, but rather might take some time to fully manifest. This behavior can be modeled using the following generalization of Equation \ref{m0134_eD}:
{\bf D} = a_0{\bf E} + a_1 \frac{\partial}{\partial t} {\bf E} + a_2 \frac{\partial^2}{\partial t^2} {\bf E} + a_3 \frac{\partial^3}{\partial t^3} {\bf E} + ... \label{m0134_ee}
where a_0, a_1, a_2, and so on are real-valued constants, and the number of terms is infinite. In practical materials, the importance of the terms tends to diminish with increasing order. Thus, it is common that only the first few terms are significant. In many applications involving common materials, only the first term is significant; i.e., a_0\approx\epsilon and a_n\approx 0 for n\ge 1. As we shall see in a moment, this distinction commonly depends on frequency.
In the phasor domain, differentiation with respect to time becomes multiplication by j\omega. Thus, Equation \ref{m0134_ee} becomes
\begin{align} \widetilde{\bf D} &= a_0\widetilde{\bf E} + a_1\left(j\omega\right)\widetilde{\bf E} + a_2\left(j\omega\right)^2\widetilde{\bf E} + a_3\left(j\omega\right)^3\widetilde{\bf E} + ... \nonumber \\ &= a_0\widetilde{\bf E} + j\omega a_1\widetilde{\bf E} - \omega^2 a_2\widetilde{\bf E} - j\omega^3 a_3\widetilde{\bf E} + ... \nonumber \\ &= \left(a_0 + j\omega a_1 - \omega^2 a_2 - j\omega^3 a_3 + ... \right) \widetilde{\bf E} \end{align} \nonumber
Note that the factor in parentheses is a complex-valued number which depends on frequency \omega and materials parameters a_0, a_1, ... We may summarize this as follows:
\widetilde{\bf D} = \epsilon_c \widetilde{\bf E} \label{m0134_eDc}
where \epsilon_c is a complex-valued constant that depends on frequency.
The notation “\epsilon_c” is used elsewhere in this book (e.g., Section 3.3) to represent a generalization of simple permittivity that accommodates loss associated with non-zero conductivity \sigma. In Section 3.3, we defined
\epsilon_c \triangleq \epsilon' -j\epsilon'' \nonumber
where \epsilon' \triangleq \epsilon (i.e., real-valued, simple permittivity) and \epsilon'' \triangleq \sigma/\omega (i.e., the effect of non-zero conductivity). Similarly, \epsilon_c in Equation \ref{m0134_eDc} can be expressed as
\epsilon_c \triangleq \epsilon' -j\epsilon'' \nonumber
but in this case
\epsilon' \triangleq a_0 - \omega^2a_2 + ... \nonumber
and
\epsilon'' \triangleq -\omega a_1 + \omega^3a_3 - ... \nonumber
When expressed as phasors, the temporal relationship between electric flux density and electric field intensity can be expressed as a complex-valued permittivity.
Thus, we now see two possible applications for the concept of complex permittivity: Modeling the delayed response of {\bf D} to changing {\bf E}, as described above; and modeling loss associated with non-zero conductivity. In practical work, it may not always be clear precisely what combination of effects the complex permittivity \epsilon_c = \epsilon'-j\epsilon'' is taking into account. For example, if \epsilon_c is obtained by measurement, both delayed response and conduction loss may be represented. Therefore, it is not reasonable to assume a value of \epsilon'' obtained by measurement represents only conduction loss (i.e., is equal to \sigma/\omega); in fact, the measurement also may include a significant frequency-dependent contribution associated with the delayed response behavior identified in this section.
An example of the complex permittivity of a typical dielectric material is shown in Figure \PageIndex{1}. Note the frequency dependence is quite simple and slowly-varying at frequencies below 1 GHz or so, but becomes relatively complex at higher frequencies.
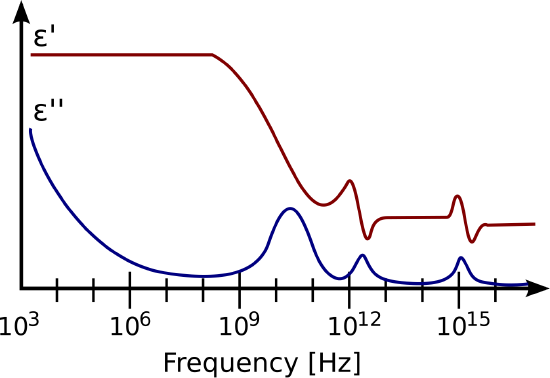 Figure \PageIndex{1}: The relative contributions of the real and imaginary components of permittivity for a typical dielectric material (in this case, a polymer). ( K.A. Mauritz modified)
Figure \PageIndex{1}: The relative contributions of the real and imaginary components of permittivity for a typical dielectric material (in this case, a polymer). ( K.A. Mauritz modified)
Additional Reading:
- “Permittivity” on Wikipedia.


