3.22: Single-Reactance Matching
( \newcommand{\kernel}{\mathrm{null}\,}\)
An impedance matching structure can be designed using a section of transmission line combined with a discrete reactance, such as a capacitor or an inductor. In the strategy presented here, the transmission line is used to transform the real part of the load impedance or admittance to the desired value, and then the reactance is used to modify the imaginary part to the desired value. (Note the difference between this approach and the quarter-wave technique described in Section 3.19. In that approach, the first transmission line is used to zero the imaginary part.) There are two versions of this strategy, which we will now consider separately.
The first version is shown in Figure 3.22.1. The purpose of the transmission line is to transform the load impedance ZL into a new impedance Z1 for which Re{Z1} = Re{Zin}. This can be done by solving the equation (from Section 3.15) Re{Z1}=Re{Z01+Γe−j2βl1−Γe−j2βl} for l, using a numerical search, or using the Smith chart.1 The characteristic impedance Z0 and phase propagation constant β of the transmission line are independent variables and can be selected for convenience. Normally, the smallest value of l that satisfies Equation ??? is desired. This value will be ≤λ/4 because the real part of Z1 spans all possible values every λ/4.
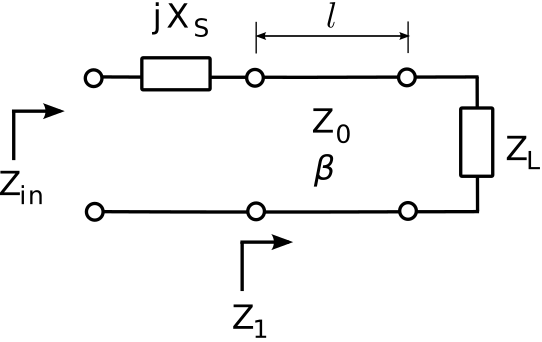 Figure 3.22.1: Single-reactance matching with a series reactance.
Figure 3.22.1: Single-reactance matching with a series reactance.
After matching the real component of the impedance in this manner, the imaginary component of Z1 may then be transformed to the desired value (Im{Zin}) by attaching a reactance Xs in series with the transmission line input, yielding Zin=Z1+jXS. Therefore, we choose Xs=Im{Zin−Z1} The sign of Xs determines whether this reactance is a capacitor (Xs<0) or inductor (Xs>0), and the value of this component is determined from Xs and the design frequency.
Design a match consisting of a transmission line in series with a single capacitor or inductor that matches a source impedance of 50Ω to a load impedance of 33.9+j17.6 Ω at 1.5 GHz. The characteristic impedance and phase velocity of the transmission line are 50Ω and 0.6c respectively.
Solution
From the problem statement: Zin≜ZS=50 Ω and ZL=33.9+j17.6 Ω are the source and load impedances respectively at f=1.5 GHz. The characteristic impedance and phase velocity of the transmission line are Z0=50 Ω and vp=0.6c respectively.
The reflection coefficient Γ (i.e., ZL with respect to the characteristic impedance of the transmission line) is
Γ≜ZL−Z0ZL+Z0≅−0.142+j0.239
The length l of the primary line (that is, the one that connects the two ports of the matching structure) is determined using the equation:
Re{Z1}=Re{Z01+Γe−j2βl1−Γe−j2βl}
where here Re{Z1}=Re{ZS}=50 Ω. So a more-specific form of the equation that can be solved for βl (as a step toward finding l) is:
1=Re{1+Γe−j2βl1−Γe−j2βl}
By trial and error (or using the Smith chart if you prefer) we find βl≅0.408 rad for the primary line, yielding Z1≅50.0+j29.0 Ω for the input impedance after attaching the primary line.
We may now solve for l as follows: Since vp=ω/β (Section 3.8), we find
β=ωvp=2πf0.6c≅52.360 rad/m
Therefore l=(βl)/β ≅ 7.8 mm.
The impedance of the series reactance should be jXs≅−j29.0 Ω to cancel the imaginary part of Z1. Since the sign of this impedance is negative, it must be a capacitor. The reactance of a capacitor is −1/ωC, so it must be true that
−12πfC≅−29.0 Ω
Thus, we find the series reactance is a capacitor of value C≅3.7pF.
The second version of the single-reactance strategy is shown in Figure 3.22.2. The difference in this scheme is that the reactance is attached in parallel. In this case, it is easier to work the problem using admittance (i.e., reciprocal impedance) as opposed to impedance; this is because the admittance of parallel reactances is simply the sum of the associated admittances; i.e., Yin=Y1+jBp where Yin=1/Zin, Y1=1/Z1, and Bp is the discrete parallel susceptance; i.e., the imaginary part of the discrete parallel admittance.
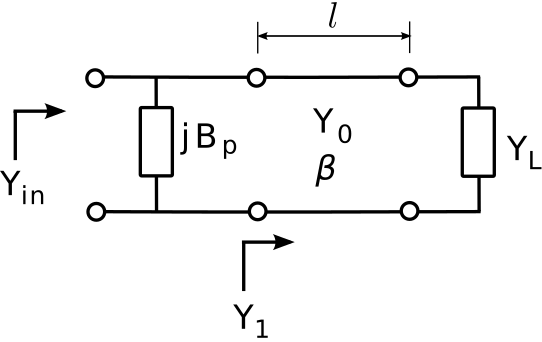 Figure 3.22.2: Single-reactance matching with a parallel reactance
Figure 3.22.2: Single-reactance matching with a parallel reactance
So, the procedure is as follows. The transmission line is used to transform YL into a new admittance Y1 for which Re{Y1} = Re{Yin}. First, we note that Y1≜1Z1=Y01−Γe−j2βl1+Γe−j2βl where Y0≜1/Z0 is characteristic admittance. Again, the characteristic impedance Z0 and phase propagation constant β of the transmission line are independent variables and can be selected for convenience. In the present problem, we aim to solve the equation Re{Y1}=Re{Y01−Γe−j2βl1+Γe−j2βl} for the smallest value of l, using a numerical search or using the Smith chart. After matching the real component of the admittances in this manner, the imaginary component of the resulting admittance may then be transformed to the desired value by attaching the susceptance Bp in parallel with the transmission line input. Since we desire jBp in parallel with Y1 to be Yin, the desired value is Bp=Im{Yin−Y1} The sign of Bp determines whether this is a capacitor (Bp>0) or inductor (Bp<0), and the value of this component is determined from Bp and the design frequency.
In the following example, we address the same problem raised in Example 3.22.1, now using the parallel reactance approach:
Design a match consisting of a transmission line in parallel with a single capacitor or inductor that matches a source impedance of 50Ω to a load impedance of 33.9+j17.6 Ω at 1.5 GHz. The characteristic impedance and phase velocity of the transmission line are 50Ω and 0.6c respectively.
Solution
From the problem statement: Zin≜ZS=50 Ω and ZL=33.9+j17.6 Ω are the source and load impedances respectively at f=1.5 GHz. The characteristic impedance and phase velocity of the transmission line are Z0=50 Ω and vp=0.6c respectively.
The reflection coefficient Γ (i.e., ZL with respect to the characteristic impedance of the transmission line) is
Γ≜ZL−Z0ZL+Z0≅−0.142+j0.239
The length l of the primary line (that is, the one that connects the two ports of the matching structure) is the solution to:
Re{Y1}=Re{Y01−Γe−j2βl1+Γe−j2βl}
where here Re{Y1}=Re{1/ZS}=0.02 mho and Y0=1/Z0=0.02 mho. So the equation to be solved for βl (as a step toward finding l) is:
1=Re{1−Γe−j2βl1+Γe−j2βl}
By trial and error (or the Smith chart) we find βl≅0.126 rad for the primary line, yielding Y1≅0.0200−j0.0116 mho for the input admittance after attaching the primary line.
We may now solve for l as follows: Since vp=ω/β (Section 3.8), we find
β=ωvp=2πf0.6c≅52.360 rad/m
Therefore, l=(βl)/β ≅ 2.4 mm.
The admittance of the parallel reactance should be jBp≅+j0.0116 mho to cancel the imaginary part of Y1. The associated impedance is 1/jBp≅−j86.3 Ω. Since the sign of this impedance is negative, it must be a capacitor. The reactance of a capacitor is −1/ωC, so it must be true that
−12πfC≅−86.3 Ω
Thus, we find the parallel reactance is a capacitor of value C≅1.2pF.
Comparing this result to the result from the series reactance method (Example 3.22.1), we see that the necessary length of transmission line is much shorter, which is normally a compelling advantage. The tradeoff is that the parallel capacitance is much smaller and an accurate value may be more difficult to achieve.
- For more about the Smith chart, see “Additional Reading” at the end of this section.↩


