5.22: Capacitance
( \newcommand{\kernel}{\mathrm{null}\,}\)
When separate regions of positive and negative charge exist in proximity, Coulomb forces (Section 5.1) will attempt to decrease the separation between the charges. As noted in Section 5.8, this can be interpreted as a tendency of a system to reduce its potential energy. If the charges are fixed in place, then the potential energy remains constant. This potential energy is proportional to the Coulomb force. Referring back to Section 5.1, the Coulomb force is:
- Proportional to quantity of positive charge squared
- Inversely proportional to the separation between the charges squared
- Inversely proportional to the permittivity of the material separating the charges
Therefore, the potential energy of the system is likewise dependent on charge, separation, and permittivity. Furthermore, we see that the ability of a system to store energy in this manner depends on the geometry of the charge distribution and the permittivity of the intervening material.
Now recall that the electric field intensity E is essentially defined in terms of the Coulomb force; i.e., F=qE (Section 2.2). So, rather than thinking of the potential energy of the system as being associated with the Coulomb force, it is equally valid to think of the potential energy as being stored in the electric field associated with the charge distribution. It follows from the previous paragraph that the energy stored in the electric field depends on the geometry of the charge distribution and the permittivity of the intervening media. This relationship is what we mean by capacitance. We summarize as follows:
Capacitance is the ability of a structure to store energy in an electric field.
and
The capacitance of a structure depends on its geometry and the permittivity of the medium separating regions of positive and negative charge.
Note that capacitance does not depend on charge, which we view as either a stimulus or response from this point of view. The corresponding response or stimulus, respectively, is the potential associated with this charge. This leads to the following definition: C≜Q+V where Q+ (units of C) is the total positive charge, V (units of V) is the potential associated with this charge (defined such that it is positive), and C (units of F) is the associated capacitance. So:
In practice, capacitance is defined as the ratio of charge present on one conductor of a two-conductor system to the potential difference between the conductors (Equation ???).
In other words, a structure is said to have greater capacitance if it stores more charge – and therefore stores more energy – in response to a given potential difference.
Figure 5.22.1 shows the relevant features of this definition.
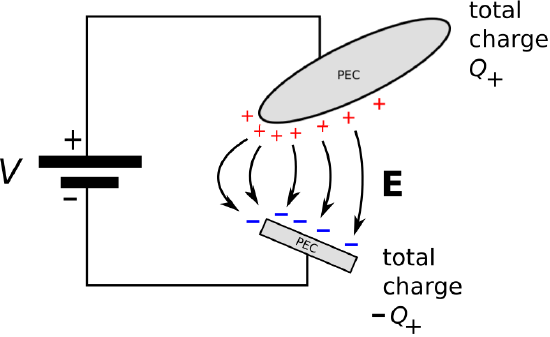 Figure 5.22.1: Electrostatic interpretation of capacitance.
Figure 5.22.1: Electrostatic interpretation of capacitance.
Here, a battery imposes the potential difference V between two regions of perfectly-conducting material. Q+ is the total charge on the surface of the PEC region attached to the positive terminal of the battery. An equal amount of negative charge appears on the surface of the PEC region attached to the negative terminal of the battery (Section 5.19). This charge distribution gives rise to an electric field. Assuming the two PEC regions are fixed in place, Q+ will increase linearly with increasing V, at a rate determined by the capacitance C of the structure.
A capacitor is a device that is designed to exhibit a specified capacitance. We can now make the connection to the concept of the capacitor as it appears in elementary circuit theory. In circuit theory, the behavior of devices is characterized in terms of terminal voltage VT in response to terminal current IT, and vice versa. First, note that current does not normally flow through a capacitor,1 so when we refer to “terminal current” for a capacitor, what we really mean is the flow of charge arriving or departing from one of the conductors via the circuit, which is equal to the flow of charge departing or arriving (respectively) at the other conductor. This gives the appearance of current flow through the capacitor when the current is examined from outside the capacitor. With that settled, we proceed as follows. Using Equation ???, we express the voltage VT across the terminals of a capacitor having capacitance C:
VT=Q+C
We seek a relationship between VT and IT. Current is charge per unit time, so the charge on either conductor is the integral of IT over time; i.e.:
Q+(t)=∫tt0IT(τ) dτ+Q+(t0)
where t0 is an arbitrarily-selected start time. In other words, amps integrated over time is charge. If we define IT as being positive in the direction of the flow of positive charge as is the usual convention, then we have:
VT(t)=1C∫tt0IT(τ) dτ+1CQ+(t0)
Again applying Equation ???, we see that the second term is simply VT(t0). This is the expected relationship from elementary circuit theory.
Finally, solving for IT we obtain the differential form of this relationship: IT(t)=CddtVT(t)
- If it does, it’s probably experiencing dielectric breakdown; see Section 5.21.↩


