13.9D: Bridge Solution by Delta-Star Transform
- Page ID
- 5858
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)In the above examples, we have calculated the condition that there is no current in the detector -. i.e. that the bridge is balanced. Such calculations are relatively easy. But what if the bridge is not balanced? Can we calculate the impedance of the circuit? Can we calculate the currents in each branch, or the potentials at any points? This is evidently a little harder. We should be able to do it. Kirchhoff’s rules and the delta-star transform still apply for alternating currents, the complication being that all impedances, currents and potentials are complex numbers.
Let us start by trying the following problem:
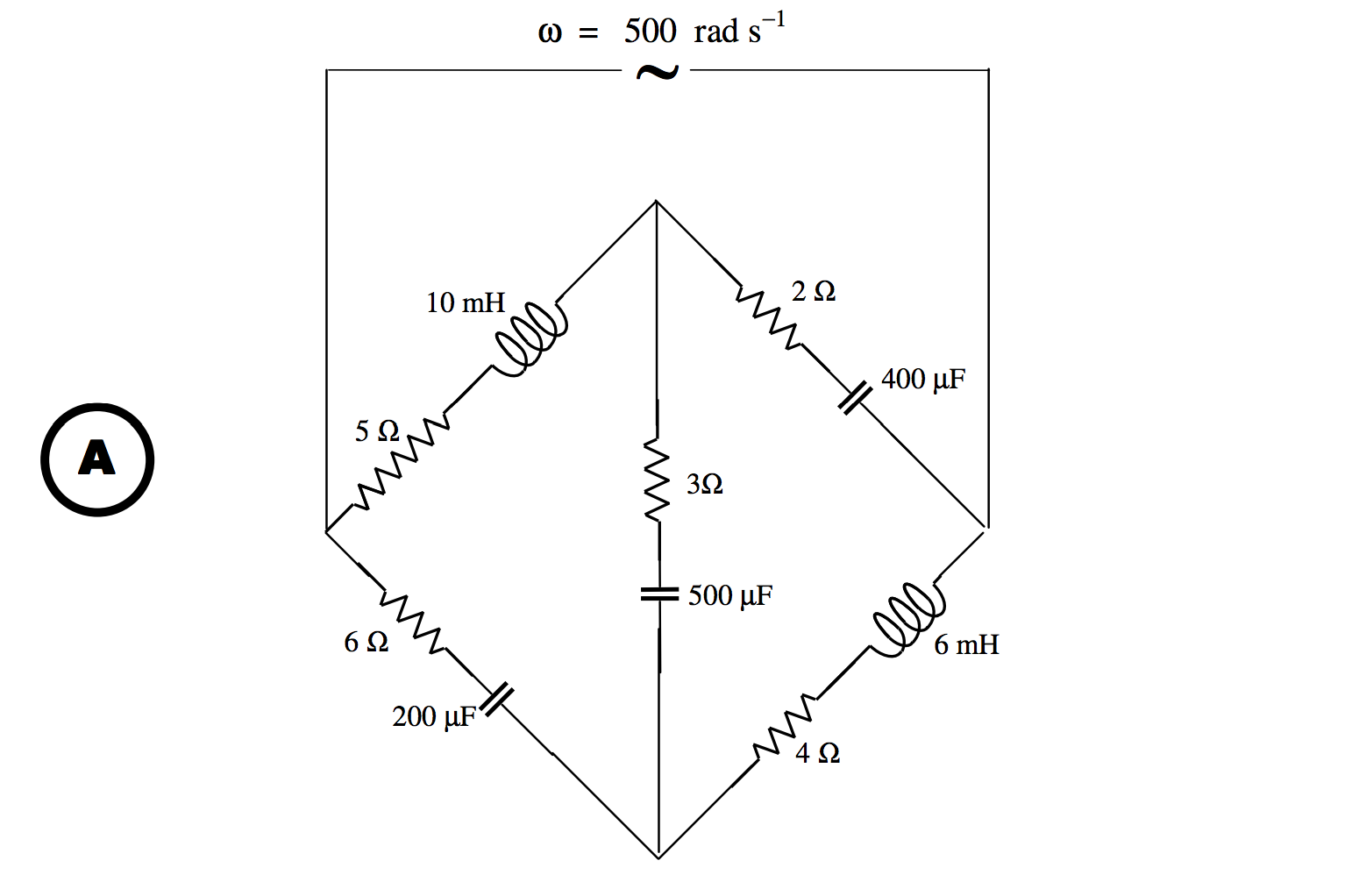
That is to say:
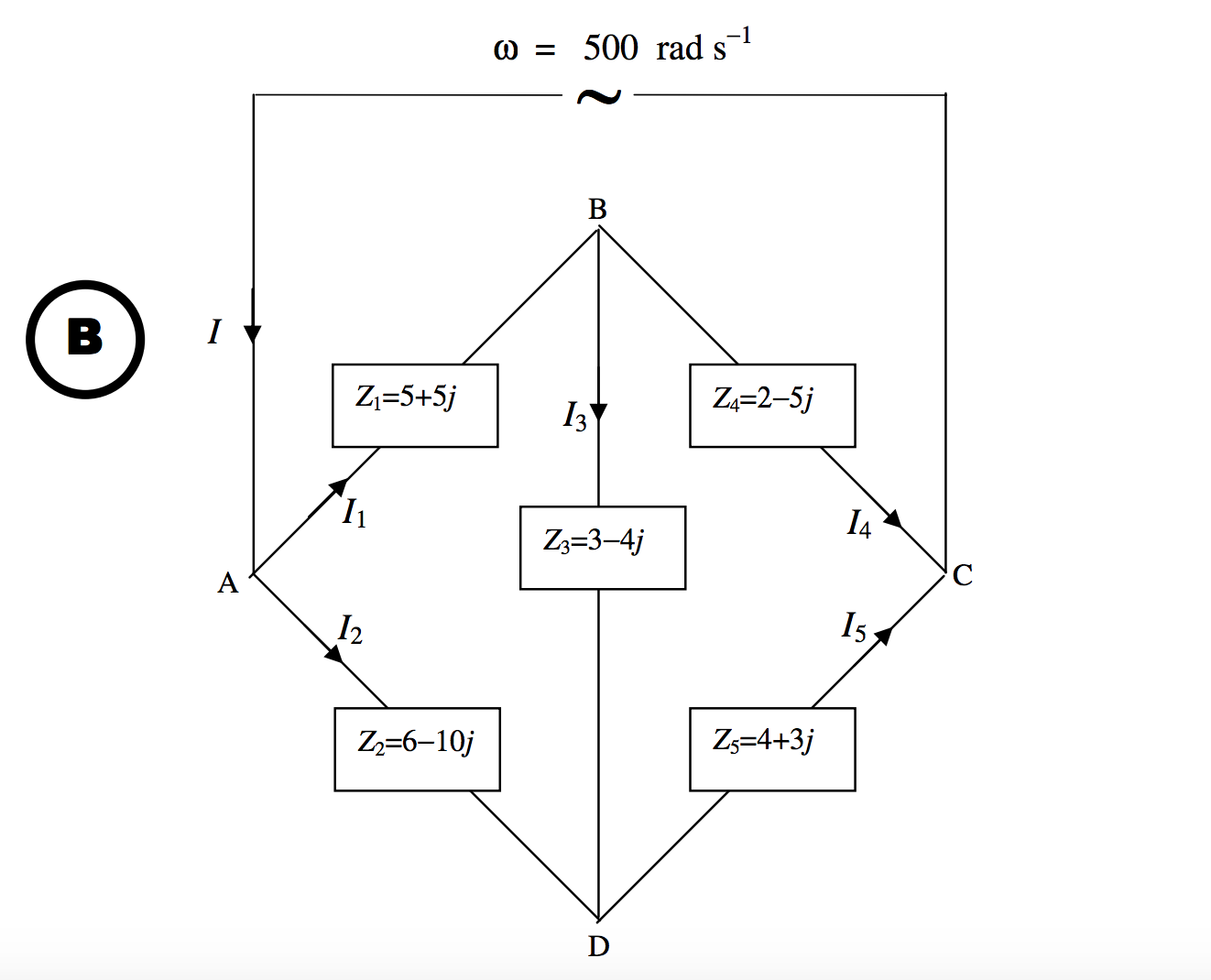
*The impedances are indicated in ohms.
Our question is: What is the impedance of the circuit at a frequency of \(\omega = 500 \text{ rad s}^{-1}\)?
We refer now to Chapter 4, Section 12. We are going to replace the left hand “delta” with its equivalent “star”. Recall equations 4.12.2 - 4.12.13. With alternating currents, We can use the same equations with alternating currents, provided that we replace the \(R_1R_2R_3G_1G_2G_3\) in the delta and the \(r_1r_2r_3g_1g_2g_3\) in the star with \(Z_1Z_2Z_3Y_1Y_2Y_3\) in the delta and \(z_1z_2z_3y_1y_2y_3\) in the star. That is, we replace the resistances with impedances, and conductances with admittances. This is going to need a little bit of calculation, and familiarity with complex numbers. I used a computer - hand calculation was too tedious and prone to mistakes. This is what I got, using \(z_1=\frac{Z_2Z_3}{Z_1+Z_2+Z_3}\) and cyclic variations:
*The impedances are indicated in ohms.
\[\begin{align}z_1&=0.642599-3.444043j \\ z_2&=1.931408+0.884477j\\ z_3&=4.693141+1.588448j \\ \end{align}\]
- The impedance of PBC is \(3.931408 - 4.115523j \, \Omega\).
- The impedance of PDC is \(4.642599 - 0.444043j \, \Omega\).
- The admittance of PBC is \(0.121364 + 0.127048j \, \text{S}\).
- The admittance of PDC is \(0.213444 + 0.020415j \, \text{S}\).
- The admittance of PC is \(0.334 808 + 0.147 463j \, \text{S}\).
- The impedance of PC is \(2.501 523 - 1.101 770j \, \Omega\).
- The impedance of AC is \(\underline{7.194 664 + 0.486 678j\, \Omega}\).
- The admittance of AC is \(0.138 359 - 0.009 359j \, \text{S}\).
Suppose the applied voltage is \(V=V_A-V_C=\hat{V}\cos \omega t\), with \(\omega = 500 \text{ rad s}^{-1}\) and \(\hat{V}= 24 \text{V}\).
Can we find the currents in each of \(Z_1,\,Z_2,\,Z_3,\,Z_4,\,Z_5,\) and the potential differences between the several points? This should be fun. I’m sitting in front of my computer. Among other things, I have trained it instantly to multiply two complex numbers and also to calculate the reciprocal of a complex number. If I ask it for \((2.3 + 4.1j)(1.9 - 3.4j)\) it will instantly tell me \(18.31 - 0.03j\). If I ask it for \(1/(0.5 + 1.2j)\) it will instantly tell me \(0.2959 - 0.7101j\). I can instantaneously convert between impedance and admittance.
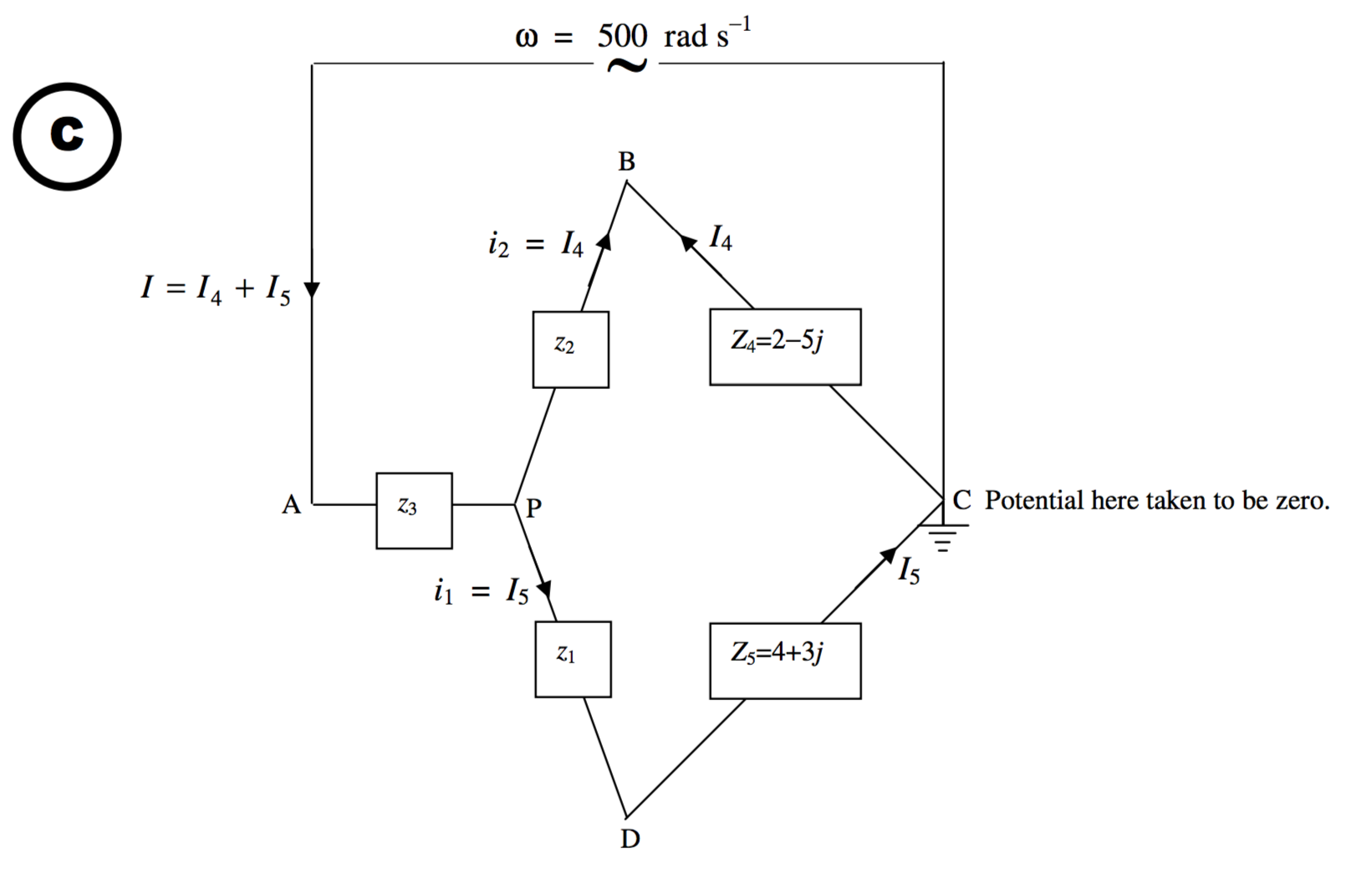
The current through any element depends on the potential difference across it. We can take any point to have zero potential, and determine the potentials at other points relative to that point. I choose to take the potential at \(\text{C}\) to be zero, and I have indicated this by means of a ground (earth) symbol at \(\text{C}\). We are going to try to find the potentials at various other points relative to that at \(\text{C}\).
In drawings B and C I have indicated the currents with arrows. Since the currents are alternating, they should, perhaps, be drawn as double-headed arrows. However, I have drawn them in the direction that I think they should be at some instant when the potential at \(\text{A}\) is greater than the potential at \(\text{C}\). If any of my guesses are wrong, I’ll get a negative answer in the usual way.
The total current \(I\) is \(V\) times the admittance of the circuit.
That is: \(I=24\times (0.138359-0.009359j)=(3.320611-0.224620j)\,\text{A}\).
The peak current will be \(3.328200 \text{ A}\) (because the modulus of the admittance is \(0.138675 \text{ S}\)), and the current lags behind the voltage by 3º.9.
I hope the following two equations are obvious from drawing C.
\[\nonumber\begin{align}&I=I_4+I_5 \\ \nonumber &I_4(z_2+Z_4)=I_5(z_1+Z_5) \\ \end{align}\]
From this,
\[\nonumber \begin{align}I_4&=\left ( \frac{z_1+Z_5}{z_1+z_2+Z_4+Z_5}\right ) I = \left (\frac{4.642599-0.444043j}{8.574007-4.559567j}\right )\times (3.320611-0.224620j) \\ \nonumber &=\underline{1.514284+0.511681j}\,\text{A}\\ \end{align}\]
\(I_4\) leads on \(V\) by 18º.7 \(\hat{I}_4=1.598397\,\text{A}\).
\(I_5=\left ( \frac{z_2+Z_4}{z_1+z_2+Z_4+Z_5}\right )I=\underline{1.806328-0.736302j \text{ A}}\)
\(I_5\) lags behind \(V\) by 22º.2 \(\hat{I}_5=1.950631\, \text{A}\).
Check: \(I_4+I_5=I \checkmark\)
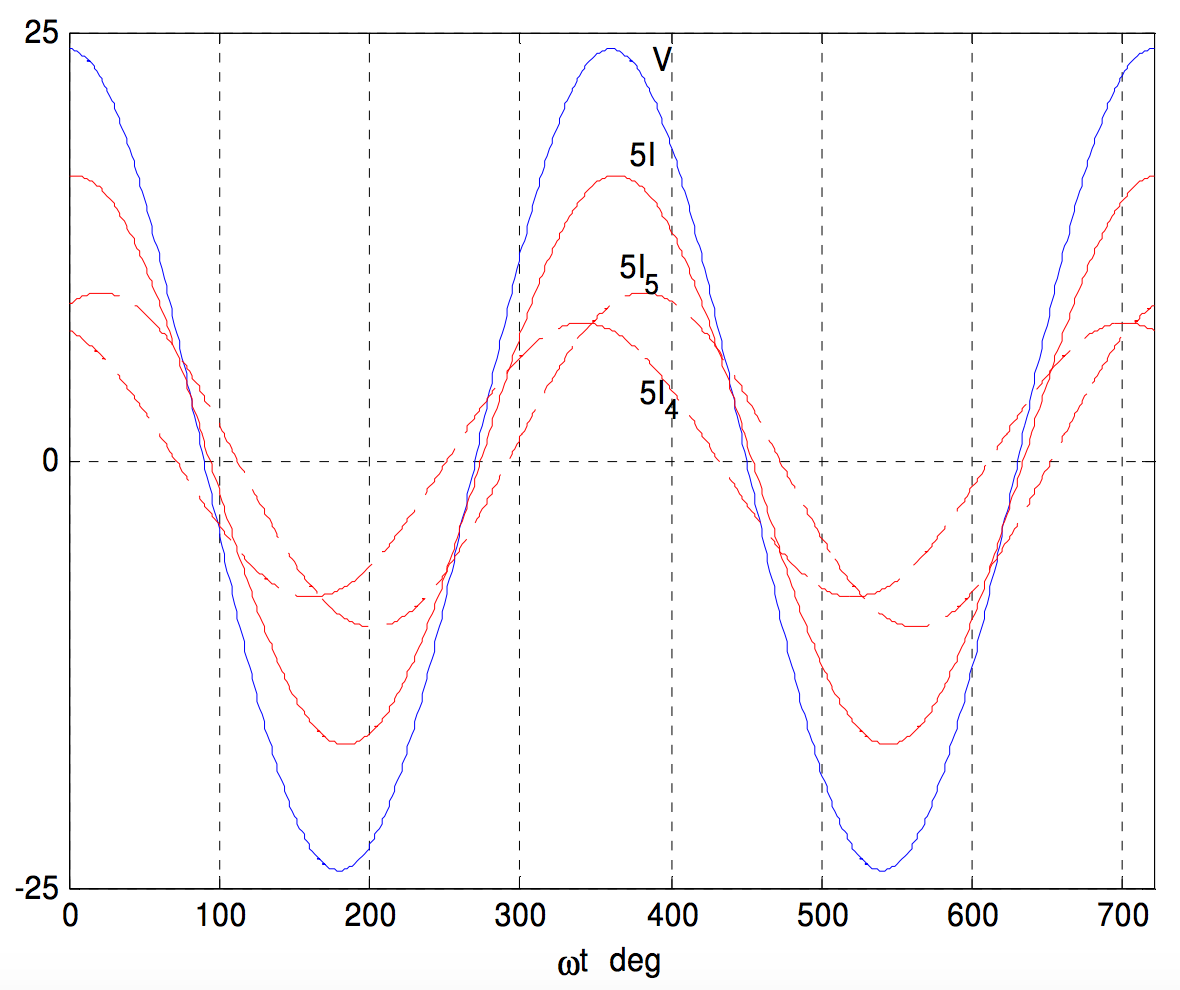
I show below graphs of the potential difference between \(\text{A}\) and \(\text{C}\) \((V=V_A-V_C)\) and the currents \(I\), \(I_4\) and \(I_5\). The origin for the horizontal scale is such that the potential at \(\text{A}\) is zero at \(t = 0\). The vertical scale is in volts for \(V_C\), and is five times the current in amps for the three currents.
We don’t really need to know \(i_1,\,i_2,\,i_3\), but we do want to know \(I_1,\,I_2,\,I_3\). Let’s first see if we can find some potentials relative to the point \(\text{C}\).
From drawing C we see that
\(V_B-V_C=V_D=I_4Z_4\), which results in \(\underline{V_B=(5.586975-6.548057j)\,\text{V}}\)
\(V_B\) lags behind \(V\) by \(0.864 432 \text{ rad }= \)49º.5 \(\hat{V}_B=8.607603 \text{ V}\).
From drawing C we see that
\(V_D-V_C=V_D=I_5Z_5\), which results in \(\underline{V_D=(9.434216+2.473775j) \text{ V}}\)
\(V_D\) leads on \(V\) by \(0.256 440 \text{ rad }=\) 14º.7 \(\hat{V}_B=9.753153 \text{ V}\).
We can now calculate \(I_3\) (see drawing B) from \(I_3=\frac{V_B-V_D}{Z_3}=(V_B-V_D)Y_3\).
I find \(\underline{I_3=0.981824-1.698178j \text{ A}}\)
\(I_3\) lags behind \(V\) by \(1.046 588 \text{ rad }=\) 60º.0. \(\hat{I}_3=1.961578 \text{ A}\).
\(I_1\) can now be found from \(I_1=\frac{V_A-V_B}{Z_1}=(V_A-V_B)Y_1\). The real part of\(V_A\) is 24 V, and (since we have grounded C), its imaginary part is zero. If in doubt about this verify that
\(IZ=(3.320611-0.224620 j)(7.194664+0.486678j)=(24+0j)\text{V}.\checkmark\)
I find
\(\underline{I_1=2.496108-1.186497 j \text{ A}}\)
\(I_1\) lags behind \(V\) by \(0.443 725 \text{ rad }= \)25º.4. \(\hat{I}_1=2.763753 \text{ A}\).
In a similar manner, I find
\(\underline{I_2=0.824503+0.961876j \text{ A}}\)
\(I_2\) leads on \(V\) by \(0.862 147 \text{ rad }=\) 49º.4. \(\hat{I}_2=1.266891 \text{ A}\).
Summary:
- \(\underline{I=3.320611-0.224620j \text{ A}}\)
- \(\underline{I_1=2.496108-1.186497j \text{ A}}\)
- \(\underline{I_2=0.824503-0.961876j \text{ A}}\)
- \(\underline{I_3=0.981824-1.698178j \text{ A}}\)
- \(\underline{I_4=1.514284-0.511681j \text{ A}}\)
- \(\underline{I_5=1.806328-0.736302j \text{ A}}\)
These may be checked by verification of Kirchhoff’s first rule at each of the points \(\text{A}\), \(\text{B}\), \(\text{C}\), \(\text{D}\).