13.6: Admittance
( \newcommand{\kernel}{\mathrm{null}\,}\)
In general, the impedance of a circuit is partly resistive and partly reactive:
Z=R+jX.
The real part is the resistance, and the imaginary part is the reactance. The relation between V and I is V=IZ. If the circuit is purely resistive, V and I are in phase. If is it purely reactive, V and I differ in phase by 90o. The reactance may be partly inductive and partly capacitive, so that
Z=R+j(XL+XC).
Indeed we shall describe such a system in detail in the next section. Note that XC is negative.
The Equation ??? is sometimes written Z=R+j(XL−XC), in which XC is intended to represent the unsigned quantity 1/(Cω). In these notes XC is intended to represent −1/(Cω).
The reciprocal of the impedance Z is the admittance, Y.
Thus
Y=1Z=1R+jX.
And of course, since V=IZ,I=VY.
Whenever we see a complex (or a purely imaginary) number in the denominator of an expression, we always immediately multiply top and bottom by the complex conjugate, so Equation ??? becomes
Y=Z∗|Z|2=R−jXR2+X2.
This can be written
Y=G+jB,
where the real part, G, is the conductance:
G=RR2+X2,
and the imaginary part, B, is the susceptance:
B=−XR2+X2.
The SI unit for admittance, conductance and susceptance is the siemens (or the "mho" in informal talk).
I leave it to the reader to show that
R=GG2+B2
and
X=−BG2+B2.
What is the impedance of the circuit below to alternating current of frequency 2000/π Hz (ω=4000 rad s−1)?
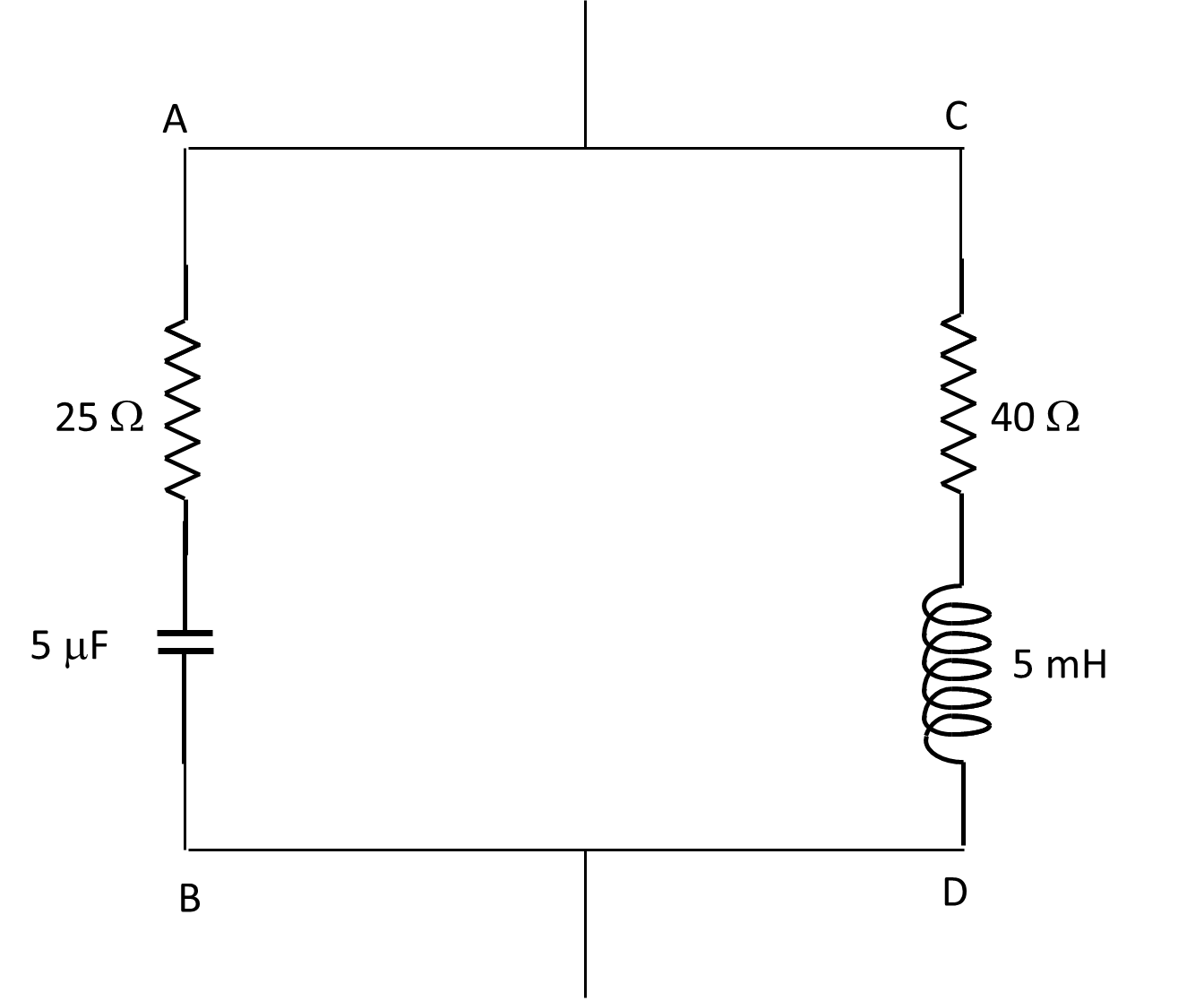
Solution
I think that the following will be readily agreed. (Remember, the admittance is the reciprocal of the impedance; and, whenever you see a complex number in a denominator, immediately multiply top and bottom by the conjugate.)
Impedance of AB=25(1−2j)Ω
Impedance of CD=20(2+j)Ω
Admittance of AB=1+2j125 S
Admittance of CD=2−j100 S
Admittance of the circuit = 28+6j1000 S
Impedance of the circuit = 100(14−3j)41Ω
The current leads on the voltage by 12º.
Three resistors and a capacitor are connected to an AC voltage source as shown. The point E is grounded (earthed), and its potential can be taken as zero. Calculate the three currents, and the potential at B.
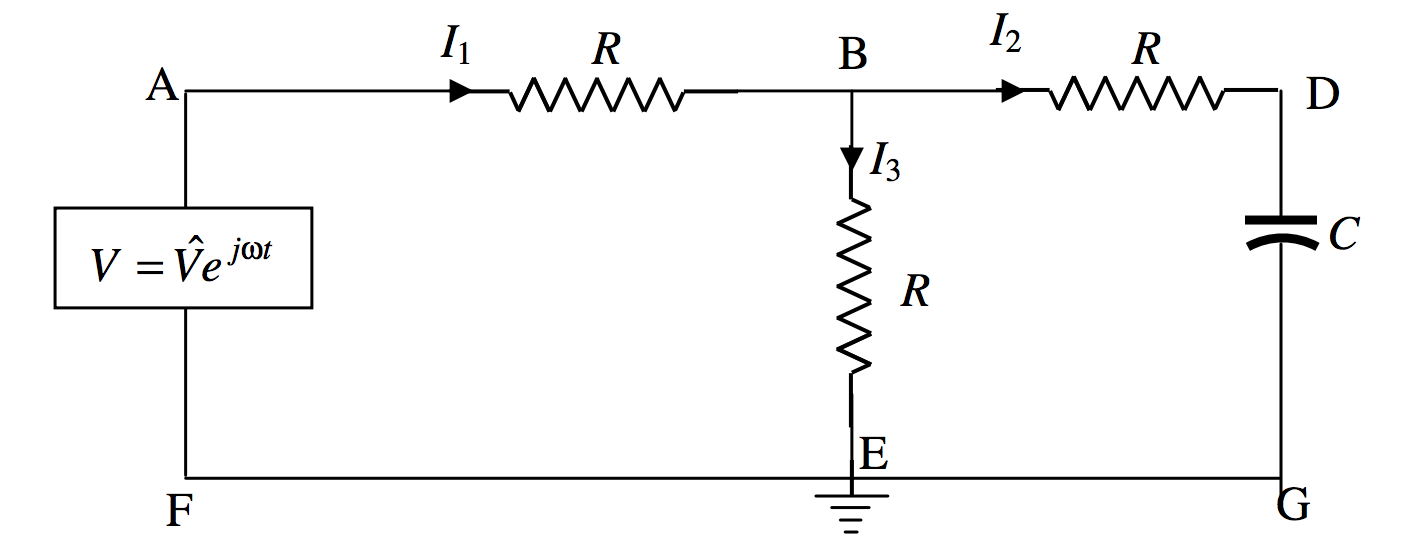
Solution
We can do this by using Kirchhoff’s rules in the usual way. When I did this I found the algebra to be slightly heavy going, and I found that it was much simplified by writing 1Cω=aR, where a is a dimensionless number. Then, instead of writing the impedance of the section BDG as R−jCω, I write it as R(1−ja).
Kirchhoff’s rules, applied to two circuits and the point B, are
V=I1R+I2R
I2(1−ja)−I3=0
I1=I2+I3
These equations are to be solved for the three currents I1,I2,I3. These will all be complex numbers, representing alternating currents. Solution could proceed, for example, by eliminating I3 from equations ??? and ???, and then eliminating I3 from equations ??? and ???. This results in two equations in I1 and I2. We can eliminate I1 from these to obtain I2. I make it I2=VR(3−2aj), but then we immediately multiply top and bottom by 3+2aj to obtain
I2=(3+2aj9+4a2)VR
It is then straightforward to return to the original equations to obtain
I1=(6+2a2+aj9+4a2)VR
and
I3=(3+2a2−aj9+4a2)VR
For example, suppose that the frequency and the capacitance were such that a=1, then
I1=(8+j13)VR
I2=(3+2j13)VR
and
I3=(5−j13)VR
Thus I1 leads on V by 7º.1; I2 leads on V by 33º.7; and I3 lags behind V by 11º.3.
The vector (phasor) diagram for these three currents is shown below, in which the phasor representing the alternating voltage V is directed along the real axis.

Bearing in mind that the potential at E is zero, we see that the potential at B is just I3R and is in phase with I3.
There is another method of finding I1, which we now try. If we get the same answer by both methods, this will be a nice check for possible mistakes in the algebra.
I’ll re-draw the circuit diagram as follows:
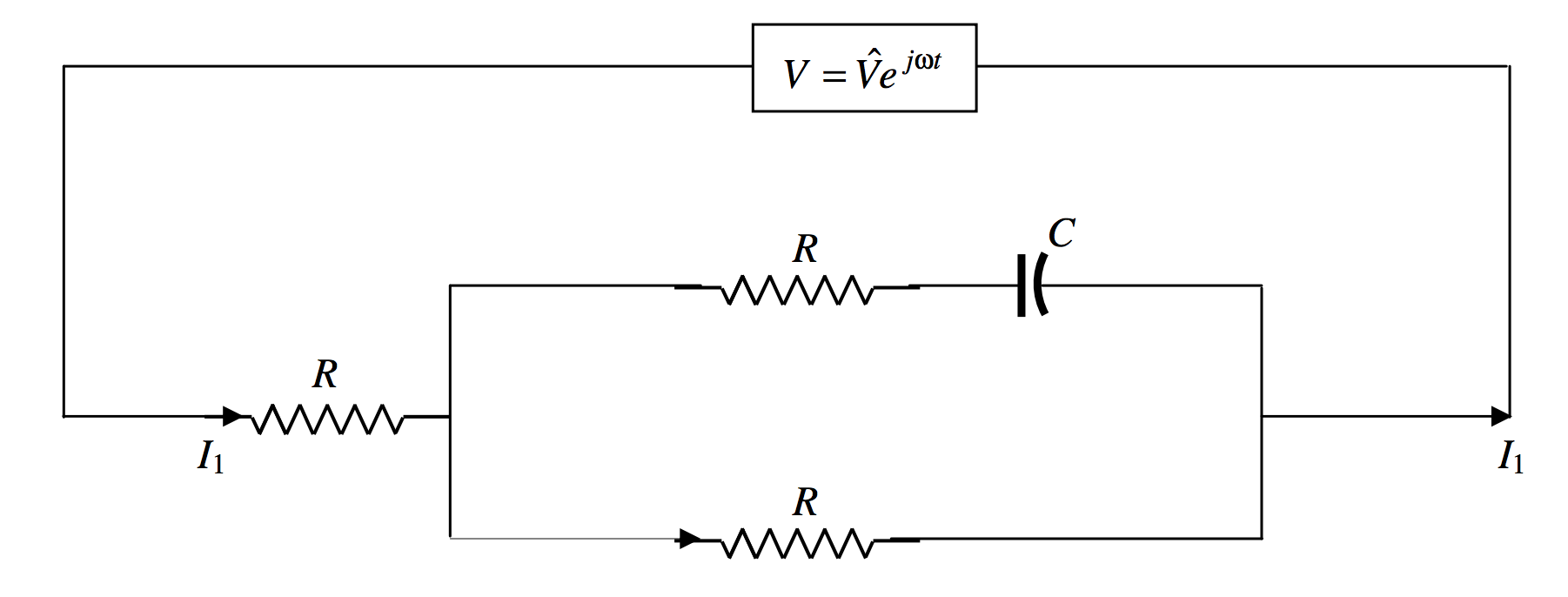
To calculate I1 we have to calculate the admittance Y of the circuit, and then we have immediately I2=YV. The impedance of R and C in series is R−jAR and so its admittance is 1R−jaR. The admittance of the rectangle is therefore 1R−jaR+1R=1R⋅[2−ja1−ja]. The impedance of the rectangle is R⋅[1−ja2−ja], and the impedance of the whole circuit is R plus this, which is R⋅[3−2ja2−ja]. The admittance of the whole circuit is 1R⋅[2−ja3−2ja]. Multiply top and bottom by the conjugate of the denominator to obtain 1R⋅[6+2a2+ja9+4a2]. Hence I1=VR⋅[6+2a2+ja9+4a2], which is what we obtained by the Kirchhoff method.
If you want to invent some similar problems, either as a student for practice, or as an instructor looking for homework or examination questions, you could generalize the above problem as follows.
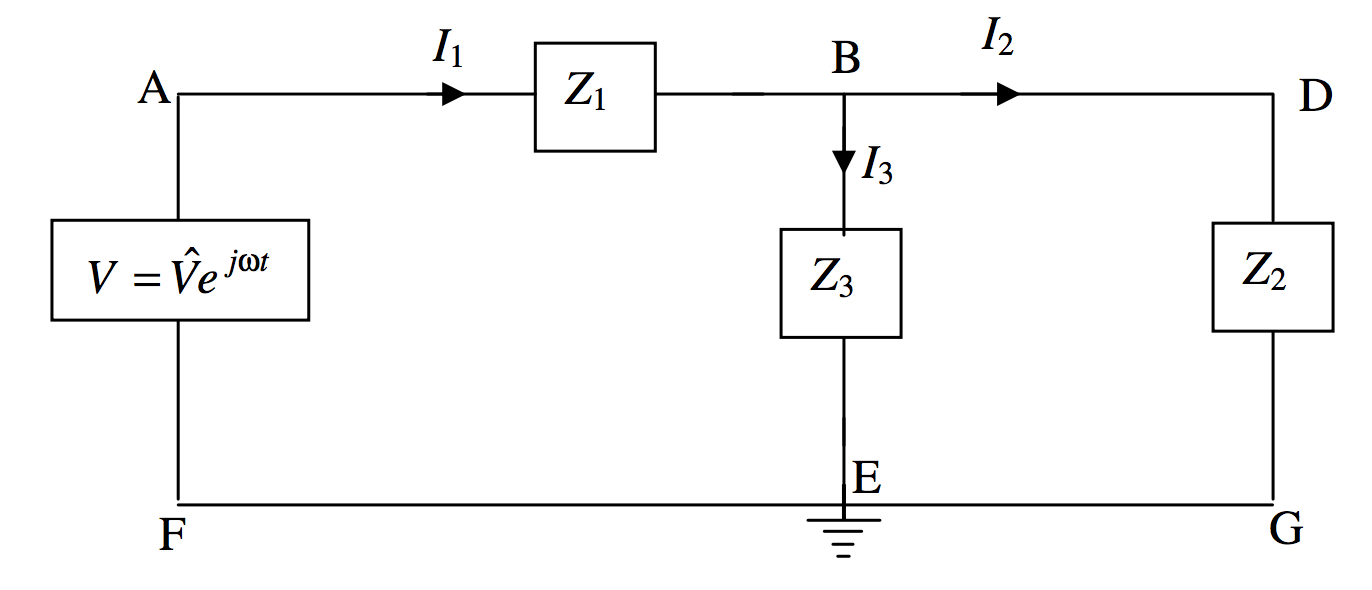
Each of the three impedances in the circuit could be various combinations of capacitors and inductors in series or in parallel, but, whatever the configuration, each could be written in the form R+jX. Three Kirchhoff equations could be constructed as follows
V=I1Z1+I3Z3
V=I1Z1+I2Z2
I1=I2+I3
If I have done my algebra correctly, I make the solutions
I1=V(Z2+Z3)Z2Z3+Z3Z1+Z1Z2
I2=VZ3Z2Z3+Z3Z1+Z1Z2
I3=VZ2Z2Z3+Z3Z1+Z1Z2
Each must eventually be written in the form ReI+jImI, or (G+jB)V. For example, suppose that the three impedances, in ohms, are Z1=2−3j,Z2=4+2j,Z3=3−3j. In that case, I believe (let me know if I’m wrong, jtatum at uvic.ca) that Equation ??? becomes, after manipulation, I3=74+152j1429V. This means that I3 leads on V by 64º.0, and that the peak value of I3 is 0.118V A, where V is in V.
The potential at B is I3Z3. Both of these are complex numbers and the potential at B us not in phase with I3 unless Z3is purely resistive.
In composing a problem, you probably want all resistances and reactances to be of comparable magnitudes, say a few ohms each. As a guide, if you choose the frequency to be 500/π Hz, so that ω=103 rad s−1, and if you choose inductances to be about 10 mH and capacitances about 100μF, your reactances will each be about 10Ω.
You can probably also compose problems with various bridge circuits, such as
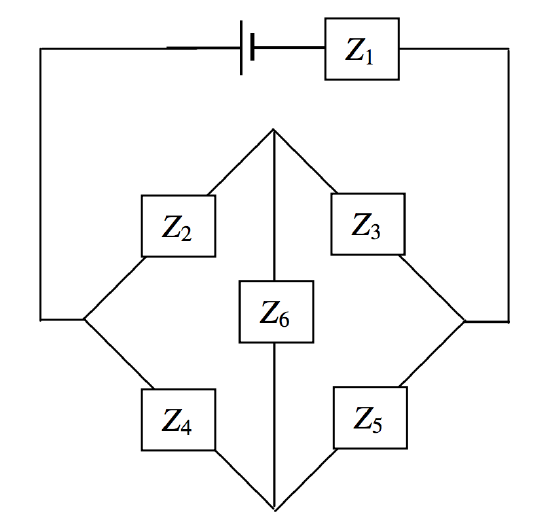
There are six independent impedances, so you’ll need six equations. Three for Kirchhoff’s second rule, to cover the complete circuit once; and three of Kirchhoff’s first rule, at three points. Good luck in solving them. Remember that, in an equation involving complex numbers, the real and imaginary parts are separately equal. And remember, as soon as a complex number appears in a denominator, multiply top and bottom with the conjugate. Alternatively, and easier, we could do what we did with a similar problem with direct currents in Section 4.12, using a delta-star transformation. We’ll try an example in Section 13.9, subsection 13.9.4.


