1.4: Exercise Problems

1. Calculate the electric field created by a thin, long, straight filament, electrically charged with a constant linear density \(\ \lambda\), using two approaches:
   1. directly from the Coulomb law, and
   2. using the Gauss law.
2. Two thin, straight parallel filaments, separated by distance \(\ \rho\), carry equal and opposite uniformly distributed charges with linear density \(\ \lambda\) – see the figure on the right. Calculate the force (per unit length) of the Coulomb interaction of the wires. Compare its dependence on \(\ \rho\) with the Coulomb law for the force
   between two point charges.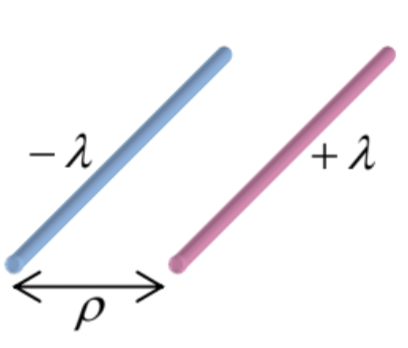

   

3. A sphere of radius \(\ R\), whose volume had been charged with a constant density \(\ \rho\), is split with a very narrow, planar gap passing through its center. Calculate the force of the mutual electrostatic repulsion of the resulting two hemispheres.
4. A thin spherical shell of radius \(\ R\), that had been charged with a constant areal density \(\ \sigma\), is split into two equal halves by a very narrow, planar cut passing through the sphere’s center. Calculate the force of electrostatic repulsion between the resulting hemispheric shells, and compare the result with that of the previous problem.
5. Calculate the distribution of the electrostatic potential created by a straight, thin filament of a finite length \(\ 2l\), charged with a constant linear density \(\ \lambda\), and explore the result in the limits of very small and very large distances from the filament.
6. A thin plane sheet, perhaps of an irregular shape, carries an electric charge with a constant areal density \(\ \sigma\).
   1. Express the electric field’s component normal to the plane, at a certain distance from it, via the solid angle \(\ \Omega\) at which the sheet is visible from the observation point.
   2. Use the result to calculate the field in the center of a cube, with one face charged with a constant density \(\ \sigma\).
7. Can one create, in an extended region of space, electrostatic fields with the Cartesian components proportional to the following products of Cartesian coordinates \(\ \{x, y, z\}\):
   1. \(\ \{y z, x z, x y\}\),
   2. \(\ \{x y, x y, y z\}\)?
8. Distant sources have been used to create different electric fields on two sides of a wide and thin metallic membrane, with a round hole of radius R in it – see the figure on the right. Besides the local perturbation created by the hole, the fields are uniform:

   

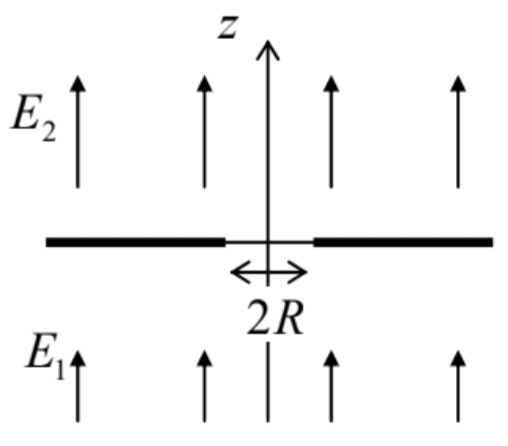
   \(\ \left.\mathbf{E}(\mathbf{r})\right|_{r>>R}=\mathbf{n}_{z} \times \begin{cases}E_{1}, & \text { at } z<0, \\ E_{2}, & \text { at } z>0 .\end{cases}\)

   Prove that the system may serve as an electrostatic lens for charged particles flying along the \(\ z\)-axis, at distances \(\ \rho<<R\) from it, and calculate the focal distance \(\ f\) of the lens. Spell out the conditions of validity of your result.

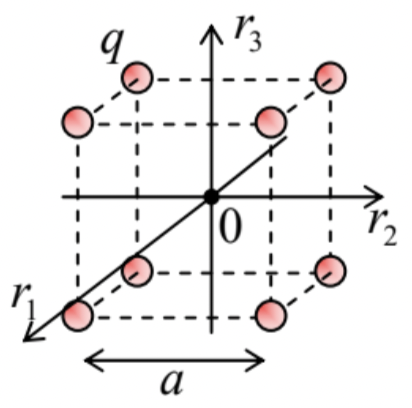
9. Eight equal point charges \(\ q\) are located at the corners of a cube of side \(\ a\). Calculate all Cartesian components \(\ E_{j}\) of the electric field, and their spatial derivatives \(\ \partial E_{j} / \partial r_{j^{\prime}}\), at the cube’s center, where \(\ r_{j}\) are the Cartesian coordinates oriented along the cube’s sides – see the figure on the right. Are all your results valid for the center of a plane square, with four equal charges in its corners?

   

10. By a direct calculation, find the average electric potential of a spherical surface of radius \(\ R\), created by a point charge \(\ q\) located at a distance \(\ r>R\) from the sphere’s center. Use the result to prove the following general mean value theorem: the electric potential at any point is always equal to its average value on any spherical surface with the center at that point, and containing no electric charges inside it.
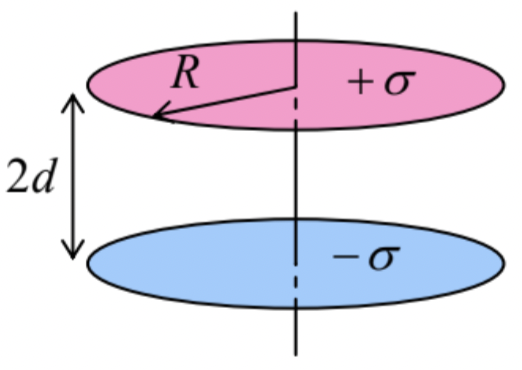
11. Two similar thin, circular, coaxial disks of radius \(\ R\), separated by distance \(\ 2d\), are uniformly charged with equal and opposite areal densities \(\ \pm \sigma\)– see the figure on the right. Calculate and sketch the distribution of the electrostatic potential and the electric field of the disks along their common axis.

    

12. In a certain reference frame, the electrostatic potential, created by some electric charge distribution, is

    \(\ \phi(\mathbf{r})=C\left(\frac{1}{r}+\frac{1}{2 r_{0}}\right) \exp \left\{-\frac{r}{r_{0}}\right\},\)

    where \(\ C\) and \(\ r_{0}\) are constants, and \(\ r \equiv|\mathbf{r}|\) is the distance from the origin. Calculate the charge distribution in space.

13. A thin flat sheet, cut in the form of a rectangle of size \(\ a \times b\), is electrically charged with a constant areal density \(\ \sigma\). Without an explicit calculation of the spatial distribution \(\ \phi(\mathbf{r})\) of the electrostatic potential induced by this charge, find the ratio of its values at the center and at the corners of the rectangle.

    Hint: Consider partitioning the rectangle into several similar parts and using the linear superposition principle.

14. Calculate the electrostatic energy per unit area of the system of two thin, parallel planes with equal and opposite charges of a constant areal density \(\ \sigma\), separated by distance \(\ d\).
15. The system analyzed in the previous problem (two thin, parallel, oppositely charged planes) is now placed into an external, uniform, normal electric field \(\ E_{\mathrm{ext}}=\sigma / \varepsilon_{0}\)– see the figure on the right. Find the force (per unit area) acting on each plane, by two methods:

    

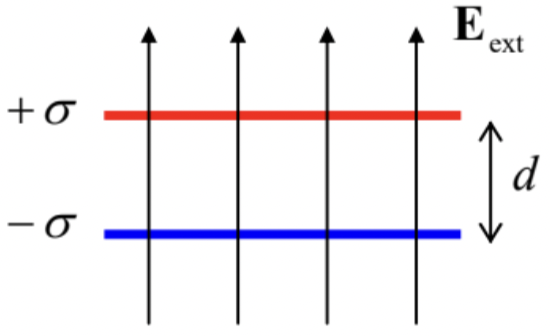
    1. directly from the electric field distribution, and
    2. from the potential energy of the system.
16. Explore the relationship between the Laplace equation (42) and the condition of the minimum of the electrostatic field energy (65).
17. Prove the following reciprocity theorem of electrostatics:²⁹ if two spatially-confined charge distributions \(\ \rho_{1}(\mathbf{r})\) and \(\ \rho_{2}(\mathbf{r})\) create respective distributions \(\ \phi_{1}(\mathbf{r})\) and \(\ \phi_{2}(\mathbf{r})\) of the electrostatic potential, then

    \(\ \int \rho_{1}(\mathbf{r}) \phi_{2}(\mathbf{r}) d^{3} r=\int \rho_{2}(\mathbf{r}) \phi_{1}(\mathbf{r}) d^{3} r.\)

    Hint: Consider integral \(\ \int \mathbf{E}_{1} \cdot \mathbf{E}_{2} d^{3} r\).

18. Calculate the energy of electrostatic interaction of two spheres, of radii \(\ R_{1}\) and \(\ R_{2}\), each with a spherically-symmetric charge distribution, separated by distance \(\ d>R_{1}+R_{2}\).
19. Calculate the electrostatic energy \(\ U\) of a (generally, thick) spherical shell, with charge \(\ Q\) uniformly distributed through its volume – see the figure on the right. Analyze and interpret the dependence of \(\ U\) on the inner cavity’s radius \(\ R_{1}\), at fixed \(\ Q\) and \(\ R_{2}\).

---

Reference

²⁹This is only the simplest one of several reciprocity theorems in electromagnetism – see, e.g., Sec. 6.8 below.