6.7: Displacement Currents

Electromagnetic induction is not the only new effect arising in non-stationary electrodynamics. Indeed, though Eqs. (21) are adequate for the description of quasistatic phenomena, a deeper analysis shows that one of these equations, namely \(\ \nabla \times \mathbf{H}=\mathbf{j}\), cannot be exact. To see that, let us take the
divergence of its both sides:

\[\ \nabla \cdot(\nabla \times \mathbf{H})=\nabla \cdot \mathbf{j}.\tag{6.89}\]

But, as the divergence of any curl,⁵⁶ the left-hand side should equal zero. Hence we get

\[\ \nabla \cdot \mathbf{j}=0.\tag{6.90}\]

This is fine in statics, but in dynamics, this equation forbids any charge accumulation, because according to the continuity relation (4.5),

\[\ \nabla \cdot \mathbf{j}=-\frac{\partial \rho}{\partial t}.\tag{6.91}\]

This discrepancy had been recognized by James Clerk Maxwell who suggested, in the 1860s, a way out of this contradiction. If we generalize the equation for \(\ \nabla \times \mathbf{H}\) by adding to the term \(\ \mathbf{j}\) (that describes the density of real electric currents) the so-called displacement current density term,

\[\ \text{Displacement current density}\quad\quad\quad\quad\mathbf{j}_{\mathrm{d}} \equiv \frac{\partial \mathbf{D}}{\partial t},\tag{6.92}\]

(which of course vanishes in statics), then the equation takes the form

\[\ \nabla \times \mathbf{H}=\mathbf{j}+\mathbf{j}_{\mathrm{d}} \equiv \mathbf{j}+\frac{\partial \mathbf{D}}{\partial t}.\tag{6.93}\]

In this case, due to the equation (3.22), \(\ \nabla \cdot \mathbf{D}=\rho\), the divergence of the right-hand side equals zero due to the continuity equation (92), and the discrepancy is removed. This incredible theoretical feat,⁵⁷ confirmed by the 1886 experiments carried out by Heinrich Hertz (see below) was perhaps the main triumph of theoretical physics of the 19^th century.

Maxwell’s displacement current concept, expressed by Eq. (93), is so important that it is worthwhile to have one more look at its derivation using a particular model shown in Fig. 10.⁵⁸

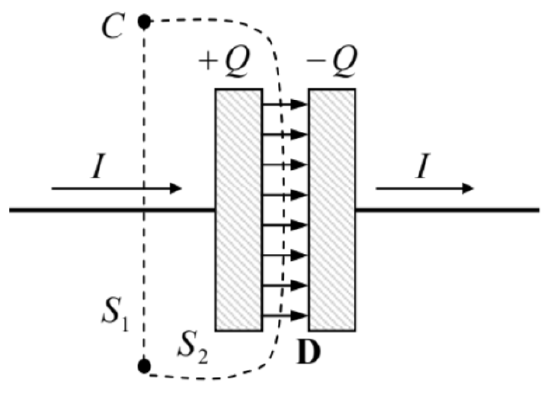Fig. 6.10. The Ampère law applied to capacitor recharging.

Neglecting the fringe field effects, we may use Eq. (4.1) to describe the relationship between the current \(\ I\) flowing through the wires and the electric charge \(\ Q\) of the capacitor:⁵⁹

\[\ \frac{d Q}{d t}=I.\tag{6.94}\]

Now let us consider a closed contour \(\ C\) drawn around the wire. (Solid points in Fig. 10 show the places where the contour intercepts the plane of the drawing.) This contour may be seen as the line limiting either the surface \(\ S_{1}\) (crossed by the wire) or the surface \(\ S_{2}\) (avoiding such crossing by passing through
the capacitor’s gap). Applying the macroscopic Ampère law (5.116) to the former surface, we get

\[\ \oint_{C} \mathbf{H} \cdot d \mathbf{r}=\int_{S_{1}} j_{n} d^{2} r=I,\tag{6.95}\]

while for the latter surface the same law gives a different result,

\[\ \oint_{C} \mathbf{H} \cdot d \mathbf{r}=\int_{S_{2}} j_{n} d^{2} r=0,\quad\quad\quad\quad \color{red}\text{[WRONG!]}\tag{6.96}\]

for the same integral. This is just an integral-form manifestation of the discrepancy outlined above, but it shows clearly how serious the problem is (or rather it was – before Maxwell).

Now let us see how the introduction of the displacement currents saves the day, considering for the sake of simplicity a plane capacitor of area \(\ A\), with a constant electrode spacing. In this case, as we already know, the field inside it is uniform, with \(\ D=\sigma\), so that the total capacitor’s charge \(\ Q=A \sigma=AD\), and the current (94) may be represented as

\[\ I=\frac{d Q}{d t}=A \frac{d D}{d t}.\tag{6.97}\]

So, instead of the wrong Eq. (96), the Ampère law modified following Eq. (93), gives

\[\ \oint_{C} \mathbf{H} \cdot d \mathbf{r}=\int_{S_{2}}\left(j_{\mathrm{d}}\right)_{n} d^{2} r=\int_{S_{2}} \frac{\partial D_{n}}{\partial t} d^{2} r=\frac{d D}{d t} A=I,\tag{6.98}\]

i.e. the Ampère integral becomes independent of the choice of the surface limited by the contour \(\ C\) – as it has to be.

---

Reference

⁵⁶ Again, see MA Eq. (11.2) – if you need it.

⁵⁷ It looks deceivingly simple now – after the fact, and with the current mathematical tools (especially the del operator), much superior to those that were available to J. Maxwell.

⁵⁸ No physicist should be ashamed of doing this. For example, J. Maxwell’s main book, A Treatise of Electricity and Magnetism, is full of drawings of plane capacitors, inductance coils, and voltmeters. More generally, the whole history of science teaches us that snobbery regarding particular examples and practical systems is a virtually certain path toward producing nothing of either practical value or fundamental importance.

⁵⁹ This is of course just the integral form of the continuity equation (91).