2.2: The geometry of the three-dimensional rotation group. The Rodrigues-Hamilton theorem

There are three types of transformations that map the Euclidean space onto itself: translations, rotations and inversions. The standard notation for the proper rotation group is $\mathcal{O}^{+}, \text {or } \mathcal{S O}(3)$ short for “simple orthogonal group in three dimensions”. “Simple” means that the determinant of the transformation is $+1$, we have proper rotations with the exclusion of the inversion of the coordinates:

$$\begin{array}{l}x \rightarrow-x \\y \rightarrow-y \\z \rightarrow-z\end{array} \label{1}$$

In contrast to the group of translations, $\mathcal{S O}(3)$ is non-Abelian, and its theory, beginning with the adequate choice of parameters is quite complicated. Nevertheless, its theory was developed to a remarkable degree during the 18th century by Euler.

Within classical mechanics the problem of rotation is not considered to be of fundamental importance. The Hamiltonian formalism is expressed usually in terms of point masses, which do not rotate. There is a built-in bias in favor of translational motion.

The situation is different in quantum mechanics where rotation plays a paramount role. We have good reasons to give early attention to the rotation group, although at this point we have to confine ourselves to a purely geometrical discussion that will be put later into an algebraic form.

According to a well known theorem of Euler, an arbitrary displacement of a rigid body with a single fixed point can be conceived as a rotation around a fixed axis which can be specified in terms of the angle of rotation $\phi$, and the unit vector $\hat{u}$ along the direction of the rotational axis. Conventionally the sense of rotation is determined by the right hand rule. Symbolically we may write $R=\{\hat{u}, \phi\}$.

The first step toward describing the group structure is to provide a rule for the composition of rotations with due regard for the noncommuting character of this operation. The gist of the argument is contained in an old theorem by Rodrigues-Hamilton.

Our presentation follows that of C. L. K. Whitney [Whi68]. Consider the products

$$R_{3}=R_{2} R_{1} \label{2}$$

$$R_{3}^{\prime}=R_{1} R_{2} \label{3}$$

where $R_{3}$ is the composite rotation in which $R_{1}$ is followed by $R_{2}$.

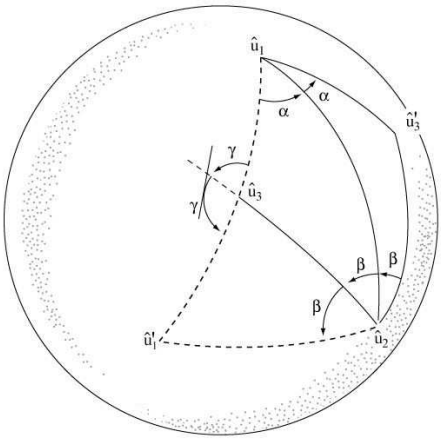
Figure 2.1 represents the unit sphere and is constructed as follows: the endpoints of the vectors $\hat{u}_{1}$ and $\hat{u}_{2}$ determine a great circle, the smaller arc of which forms the base of mirror-image triangles having angles $\phi_{1} / 2 \text { and } \phi_{2} / 2$ as indicated. The endpoint of the vector $\hat{u}_{1}^{\prime}$ is located by rotating $\hat{u}_{1}$ by angle $\phi_{2} \text { about } \hat{u}_{2}$. Our claim, that the other quantities appearing on the figure are legitimately labeled $\phi_{3} / 2, \hat{u}_{3}, \hat{u}_{3}^{\prime}$ is substantiated easily. Following the sequence of operations indicated in 2.2.3, we see that the vector called $\hat{u}_{3}$ is first rotated by angle $\phi_{1}, \text { about } \hat{u}_{1}$, which takes in into $\hat{u}_{3}^{\prime}$. Then it is rotated by angle $\phi_{2} \text { about } \hat{u}_{2} \text { , which takes it back to } \hat{u}_{3}$. Since it is invariant, it is indeed the axis of the combined rotation. Furthermore, we see that the first rotation leaves $\hat{u}_{1}$ invariant and the second rotation, that about $\hat{u}_{2}$ carries it into $\hat{u}_{1}^{\prime}$, the position it would reach if simply rotated about $\hat{u}_{3}, \text { by the angle called } \phi_{3}$. Thus that angle is indeed the angle of the combined rotation. Note that a symmetrical argument shows that $\hat{u}_{3}^{\prime} \text { and } \phi_{3} \text { are the axis and angle of the rotation } P_{3}^{\prime}=R_{1} R_{2}$.

Equation $\ref{3}$ can be expressed also as

$$R_{3}^{-1} R_{2} R_{1}=1\label{4}$$

which is interpreted as follows: rotation about $\hat{u}_{1}, \text { by } \phi_{1}$, followed by rotation about $\hat{u}_{2}, \text { by } \phi_{2}$ followed by rotation about $\hat{u}_{3}, \text { by minus } \phi_{3}$ produces no change. This statement is the Rodrigues-Hamilton theorem.

Figure 2.1: Composition of the Rotations of the Sphere $\alpha=\phi_{1} / 2, \beta=\phi_{2} / 2, \gamma=\phi_{3} / 2$.