8.4: Branch Cuts for General Multi-Valued Operations

Having discussed the simplest multi-valued operations, \(z^p\) and \(\ln(z)\), here is how to assign branch cuts for more general multi-valued operations. This is a two-step process:

1. Locate the branch points.

2. Assign branch cuts in the complex plane, such that:
   • Every branch point has a branch cut ending on it.

   • Every branch cut ends on a branch point.

   Note that any branch point lying at infinity must also obey these rules. The branch cuts should not intersect.

The choice of where to place branch cuts is not unique. Branch cuts are usually chosen to be straight lines, for simplicity, but this is not necessary. Different choices of branch cuts correspond to different ways of partitioning the values of the multi-valued operation into separate branches.

An important example

We can illustrate the process of assigning branch cuts, and defining branch functions, using the following nontrivial multi-valued operation: \[f(z) = \ln\left(\frac{z+1}{z-1}\right).\] This is multi-valued because of the presence of the complex logarithm. The branch points are \(z = 1\) and \(z = -1\), as these are the points where the input to the logarithm becomes \(\infty\) or \(0\) respectively. Note that \(z = \infty\) is *not* a branch point; at \(z = \infty\), the input to the logarithm is \(-1\), which is not a branch point for the logarithm.

We can assign any branch cut that joins these two. A convenient choice is shown below:

Figure \(\PageIndex{1}\)

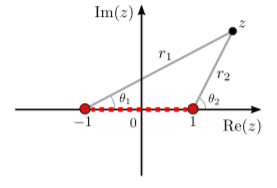
This choice of branch cut is nice because we can express the \(z+1\) and \(z - 1\) terms using the polar representations \[\begin{align} z + 1 &= r_1\,e^{i\theta_1}, \\ z - 1 &= r_2\, e^{i\theta_2},\end{align}\] where \(r_1\), \(r_2\), \(\theta_1\), and \(\theta_2\) are shown graphically in the above figure. The positioning of the branch cut corresponds to a particular choice for the ranges of the complex arguments \(\theta_1\) and \(\theta_2\). As we’ll shortly see, the present choice of branch cut corresponds to \[\theta_1 \in (-\pi,\pi), \quad \theta_2 \in (-\pi,\pi).\] Hence, in terms of this polar representation, \(f(z)\) can be written as \[\begin{align} \begin{aligned} f(z) = \ln\left(\frac{r_1}{r_2}\right) + i(\theta_1 - \theta_2 + 2\pi m), \quad m\in\mathbb{Z}, \\ \mathrm{where}\; z = -1 + r_1\,e^{i\theta_1} = 1 + r_2\,e^{i\theta_2},\quad\theta_1, \theta_2 \in (-\pi,\pi). \end{aligned}\end{align}\] The choice of \(m\) specifies the branch, and we can choose \(m = 0\) as the principal branch.

Let’s now verify that setting \(\theta_1 \in (-\pi,\pi)\) and \(\theta_2 \in (-\pi,\pi)\) is consistent with our choice of branch cut. Consider the principal branch, and compare the outputs of the above formula for \(z\) just above the real axis, and for \(z\) just below the real axis. There are three cases of interest. Firstly, for \(\mathrm{Re}(z) < 1\) (to the left of the leftmost branch point), \[\begin{align} \mathrm{Im}(z) &= 0^+ \;\;\Rightarrow\;\; f(z) = \ln\left(\frac{r_1}{r_2}\right) + i\Big((\pi) - (\pi)\Big) \quad = \ln\left(\frac{r_1}{r_2}\right) \\ \mathrm{Im}(z) &= 0^- \;\;\Rightarrow \;\; f(z) = \ln\left(\frac{r_1}{r_2}\right) + i\Big((-\pi) - (-\pi)\Big) = \ln\left(\frac{r_1}{r_2}\right).\end{align}\] Thus, there is no discontinuity along this segment of the real axis.

Secondly, for \(-1 < \mathrm{Re}(z) < 1\) (between the two branch points), \[\begin{align} \mathrm{Im}(z) &= 0^+ \;\;\Rightarrow\;\; f(z) = \ln\left(\frac{r_1}{r_2}\right) + i\Big((0) - (\pi)\Big) \;\;= \ln\left(\frac{r_1}{r_2}\right) -i\pi \\ \mathrm{Im}(z) &= 0^- \;\;\Rightarrow\;\; f(z) = \ln\left(\frac{r_1}{r_2}\right) + i\Big((0) - (-\pi)\Big) = \ln\left(\frac{r_1}{r_2}\right) + i\pi.\end{align}\] Hence, in the segment between the two branch points, there is a discontinuity of \(\pm 2\pi i\) on different sides of the real axis. The value of this discontinuity is exactly equal, of course, to the separation between the different branches of the complex logarithm.

Finally, for \(\mathrm{Re}(z) > 1\) (to the right of the rightmost branch point), there is again no discontinuity: \[\begin{align} \mathrm{Im}(z) &= 0^+ \;\;\Rightarrow\;\; f(z) = \ln\left(\frac{r_1}{r_2}\right) + i\Big((0) - (0)\Big) = \ln\left(\frac{r_1}{r_2}\right) \\ \mathrm{Im}(z) &= 0^- \;\;\Rightarrow\;\; f(z) = \ln\left(\frac{r_1}{r_2}\right) + i\Big((0) - (0)\Big) = \ln\left(\frac{r_1}{r_2}\right).\end{align}\]