10.6: Common Fourier Transforms

To accumulate more intuition about Fourier transforms, let us examine the Fourier transforms of some interesting functions. We will just state the results; the calculations are left as exercises.

Damped waves

We saw in Section 10.2 that an exponentially decay function with decay constant \(\eta \in \mathbb{R}^+\) has the following Fourier transform: \[f(x) = \left\{\begin{array}{cl}e^{-\eta x}, & x \ge 0 \\ 0, & x < 0,\end{array}\right. \;\; \overset{\mathrm{FT}}{\longrightarrow} \;\; F(k) = \frac{-i}{k-i\eta}.\] Observe that \(F(k)\) is given by a simple algebraic formula. If we “extend” the domain of \(k\) to complex values, \(F(k)\) corresponds to an analytic function with a simple pole in the upper half of the complex plane, at \(k = i\eta\).

Next, consider a decaying wave with wave-number \(q \in \mathbb{R}\) and decay constant \(\eta \in \mathbb{R}^+\). The Fourier transform is a function with a simple pole at \(q + i \eta\): \[f(x) = \left\{\begin{array}{cl}e^{i (q + i\eta) x}, & x \ge 0 \\ 0, & x < 0.\end{array}\right. \;\; \overset{\mathrm{FT}}{\longrightarrow} \;\; F(k) = \frac{-i}{k-(q + i\eta)}.\]

On the other hand, consider a wave that grows exponentially with \(x\) for \(x < 0\), and is zero for \(x > 0\). The Fourier transform is a function with a simple pole in the lower half-plane: \[f(x) = \left\{\begin{array}{cl}0, & x \ge 0 \\ e^{i (q - i\eta) x}, & x < 0.\end{array}\right. \;\; \overset{\mathrm{FT}}{\longrightarrow} \;\; F(k) = \frac{i}{k-(q - i\eta)}.\] From these examples, we see that oscillations and amplification/decay in \(f(x)\) are related to the existence of poles in the algebraic expression for \(F(k)\). The real part of the pole position gives the wave-number of the oscillation, and the distance from the pole to the real axis gives the amplification or decay constant. A decaying signal produces a pole in the upper half-plane, while a signal that is increasing exponentially with \(x\) produces a pole in the lower half-plane. In both cases, if we plot the Fourier spectrum of \(|F(k)|^2\) versus real \(k\), the result is a Lorentzian peak centered at \(k = q\), with width \(2\eta\).

Gaussian wave-packets

Consider a function with a decay envelope given by a Gaussian function: \[f(x) = e^{iq x} \, e^{-\gamma x^2}, \;\;\;\mathrm{where}\; q \in \mathbb{C},\; \gamma \in \mathbb{R}.\] This is called a Gaussian wave-packet. The width of the envelope is usually characterized by the Gaussian function’s standard deviation, which is where the curve reaches \(e^{-1/2}\) times its peak value. In this case, the standard deviation is \(\Delta x = 1/\sqrt{2\gamma}\).

We will show that \(f(x)\) has the following Fourier transform: \[F(k) = \sqrt{\frac{\pi}{\gamma}} \, e^{-\frac{(k-q)^2}{4\gamma}}.\]

To derive this result, we perform the Fourier integral as follows: \[\begin{align} F(k) &= \int_{-\infty}^\infty dx \, e^{-ikx}\, f(x) \\ &= \int_{-\infty}^\infty dx \, \exp\left\{-i(k-q)x -\gamma x^2\right\}.\end{align}\] In the integrand, the expression inside the exponential is quadratic in \(x\). We complete the square: \[\begin{align} F(k) &= \int_{-\infty}^\infty dx \, \exp\left\{-\gamma\left(x + \frac{i(k-q)}{2\gamma}\right)^2 + \gamma\left(\frac{i(k-q)}{2\gamma}\right)^2\right\} \\ &= \exp\left\{ - \frac{(k-q)^2}{4\gamma}\right\}\; \int_{-\infty}^\infty dx \, \exp\left\{-\gamma\left(x + \frac{i(k-q)}{2\gamma}\right)^2\right\}.\end{align}\] The remaining integral is the Gaussian integral with a constant imaginary shift in \(x\). By shifting the integration variable, one can show that this is equal the standard Gaussian integral, \(\sqrt{\pi/\gamma}\); the details are left as an exercise. We thus arrive at the result stated above.

The Fourier spectrum, \(|F(k)|^2\), is a Gaussian function with standard deviation \[\Delta k = \frac{1}{\sqrt{2(1/2\gamma)}} = \sqrt{\gamma}.\]

Figure \(\PageIndex{1}\)

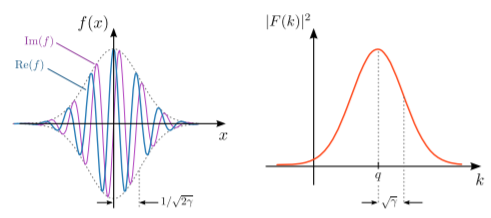
Once again, the Fourier spectrum is peaked at a value of \(k\) corresponding to the wave-number of the underlying sinusoidal wave in \(f(x)\), and a stronger (weaker) decay in \(f(x)\) leads to a broader (narrower) Fourier spectrum. These features can be observed in the plot above.