Compressed-Format Compared to Regular-Format In a First Year University Physics Course
- Page ID
- 5392
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)I. INTRODUCTION
At the University of Toronto our first year Physics course intended primarily for students in the life sciences is PHY131. We have compared the performance of PHY131 students in the regular fall 12-week term to a compressed 6-week format in the summer term: the fall version was given in 2012 and the summer version in 2013. There is also a 12-week version of the course given in the winter term, which is not part of this study. In addition, there is a separate first-year course for physics majors and specialists, and another for engineering science students: neither of these courses are part of this study.
We measured student performance using the Force Concept Inventory (FCI). The FCI has become a common tool for assessing students’ conceptual understanding of mechanics, and for assessing the effectiveness of instruction. It was introduced by Hestenes, Wells, and Swackhammer in 1992,1 and was updated in 1995.2 The FCI has now been given to many thousands of students at a number of institutions worldwide. A common methodology is to administer the instrument at the beginning of a course, the “PreCourse,” and again at the end, the “Post-Course,” and look at the gain in performance. Our students were given one-half a point, 0.5%, towards their final grade in the course for answering all questions on the Pre-Course FCI, regardless of what they answered, and given another half point for answering all questions on the Post-Course FCI, also regardless of what they answered. Below all FCI scores are given as a percent.
PHY131 is the first of a two-semester calculus-based sequence, and the textbook is by Knight.3 A senior-level high-school physics course (“Grade 12 Physics”) is recommended as a pre-requisite but is not required to take this course. One of us (JJBH) was one of the two lecturers in the fall session, and DMH was the sole lecturer in the summer session. In the fall session the two lecturers alternate so all students are given instruction by the same lecturers. Research-based instruction is used throughout the course; clickers, Peer Instruction, 4 and Interactive Lecture Demonstrations5 are used extensively in the classes. In the fall term there are two one-hour classes every week, while the summer course has two 2-hour classes per week in a single session. In addition, due to logistic constraints the summer course has a total of 22 hours of classes, while the fall version has 24 hours of classes.
Traditional tutorials and laboratories have been combined into a single active-learning environment, which we call Practicals; 6 these are inspired by Physics Education Research tools such as McDermott’s Tutorials in Introductory Physics 7 and Laws’ Workshop Physics. 8 These Practicals are similar in many ways to the Labatorials at the University of Calgary.9 In the Practicals students work in teams of four on conceptually based activities using a guided-discovery model of instruction. Whenever possible the activities use a physical apparatus or a simulation. Some of the materials are based on activities from McDermott and from Laws. In the fall term there is one 2-hour Practical every week, and the summer course has two 2-hour Practicals per week.
II. METHODS
The FCI was given during the Practicals, the Pre-Course one during the first week of classes and the Post-Course one during the last week of classes. For both courses, over 95% of the students who were currently enrolled took the FCI. For the Fall 2012 session, 868 students took the Pre-Course and 663 students took the Post-Course; for the Summer 2013 session 239 students took the Pre-Course and 193 students took the Post-Course. The students who took the Pre-Course but not the Post-Course FCI were almost all students who had dropped the course. These dropout rates, 24% for the fall session and 19% for the summer one, are typical for this course.
There is a small issue involving the values to be used in analyzing both the Pre-Course and the Post-Course FCI numbers. Below we will only analyze the data for students who took both the Pre-Course and Post-Course FCI—the “matched” values—which consisted of 641 students for the fall term and 190 for the summer term. The students who took the Post-Course FCI but not the Pre-Course FCI were probably either late enrollees or they missed the first Practical for some other reason. In all cases, the difference in median FCI scores between using raw data or matched data is only a few percent. These small differences between matched and unmatched data are consistent with a speculation by Hake for courses with enrollments of greater than 50 students.10
Figure 1 shows the FCI scores for the fall term and Fig. 2 shows the scores for the summer term. None of the histograms conform to a Gaussian distribution, especially for 3 the Post-Course results. Therefore, characterizing the results by the mean value is not appropriate, and the median value will provide a better measure of central tendency and is what we will use below, although for our data the differences in FCI scores between the means and medians is fairly small, between 0.8% and 2.6%. The uncertainty in the median is taken to be the inter-quartile range divided by \(\sqrt{N}\). 11


We also calculated gains on the FCI. The standard way of measuring student gains is from a seminal paper by Hake.12 It is defined as the gain normalized by the maximum possible gain:
\[G = \frac{Post\%− Pre\%}{100 − Pre\%} \tag{1} \]
Clearly, G cannot be calculated for Pre-Course scores of 100, which was the case for nine students in the fall term and none in the summer.
One hopes that the students’ performance on the FCI is higher at the end of a course than at the beginning. The standard way of measuring the gain in FCI scores for a class is called the average normalized gain, to which we will give the symbol mean, and was also defined by Hake in Ref. 12:
\[< g >_{mean}= \frac{< Post\% > − < Pre\% >} {100− < Pre\% > }, \tag{2} \]
where the angle brackets indicate means. However, as discussed, since the distribution of FCI scores is not Gaussian, the mean is not the most appropriate way of characterizing FCI results. We will instead report < g >median , which is also defined by Eq. (2) except that the angle brackets on the right hand side indicate medians instead of means. The normalized gains are often taken to be a measure of the effectiveness of instruction.
The uncertainties in the average and median normalized gains reported below are the propagated errors in the Pre-Course and Post-Course FCI scores. Since both of these are errors of precision, they should be combined in quadrature, i.e. the square root of the sum of the squares of the uncertainties in the Pre-Course and Post-Course scores. Therefore,
\[\Delta (< g >) = \sqrt{(\frac{∂ < g > }{∂ < Pre\%>} \Delta < Pre\%> )^2 + (\frac{∂ < g >}{ ∂ < Post\%> }\Delta < Post\%> )^2} \]
\[= \sqrt{(\frac{< Post\%> −100}{ (< Pre\%> −100)^ 2} \Delta < Pre\%> )^2 + (\frac{\Delta < Post\%> }{100− < Pre\%>} )^2} , \tag{3}\]
where Δ < Pre% > and Δ < Post% > are the inter-quartile ranges divided by N . In addition to the FCI, we collected data on student background and why they were taking the course. In the fall session we collected that data using clickers in the second week of classes: only about 500 of the 641 “matched” students answered these questions. In the summer session we avoided this unfortunate loss of 22% of the sample by including the questions as part of the Pre-Course FCI.
III. RESULTS
From Figs. 1 and 2, we can see that the summer students begin and end the course with less conceptual understanding of classical mechanics than their counterparts in the fall session. In addition, the FCI results are also reported in Table I, along with the median normalized gains. The table shows that in terms of median , the fall session outperformed the summer session by 0.14 ± 0.06 . The value of 0.14 is roughly double the uncertainty of 0.06, so the value is significant at roughly a 95% confidence interval.13 Calculating mean as is standard in the literature gives values of 0.45 ± 0.02 for the 5 fall session and 0.34 ± 0.03for the summer session, where the uncertainties are the propagated standard errors of the mean, σ / N . These values are both consistent with those of first year university courses using reformed research-based pedagogy, as can be seen, for example, in Ref. 12.
Earlier we stated that the difference between using “matched” students who took both the Pre-Course and Post-Course FCI compared to using all the FCI scores was only a few percent. As an example, for the summer 2013 session the median normalized gain using all FCI scores was 0.42 ± 0.04 .
Another way to investigate the difference in gains in the two sessions is to look at the individual normalized gains G. Figure 3 shows histograms of the gains for the fall term (panel a) and the summer term (panel b). The median values for the G values are given in the final row of Table I. The difference in the median values of G is 0.15 ± 0.04 , which is about the same as the differences in median .
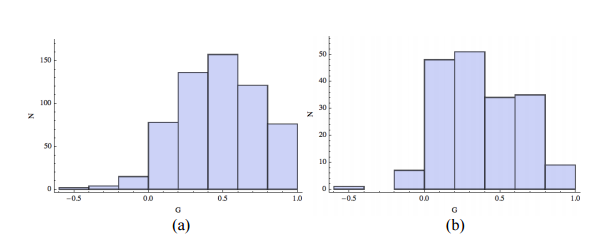
An alternative to histograms for visually comparing two distributions is the boxplot. Figure 4 shows the boxplot for the two distributions of G. The “waist” on the box plot is the median, the “shoulder” is the upper quartile, and the “hip” is the lower quartile. The vertical lines extend to the largest/smallest value less/greater than a heuristically defined outlier cutoff.14 The dots represent data that are considered to be outliers. Also shown in the figure are the statistical uncertainties in the value of the medians.
There were 10 students in the fall session whose Pre-Course score was over 80% and whose G was less than -0.66; one such student had a G of -4 and two had Gs of -3. These students were clearly outliers, and probably just “blew off” the Post-Course FCI. There were no such students in the summer session. We have chosen a range for the vertical axis in Fig. 4 so that those 10 students are not shown.

Table I. Values of FCI scores and gains for the two sessions
| Fall 2012 Summer 2013 | Summer 2013 | |
|---|---|---|
| Pre-Course FCI Medians | 50.0 ±1.3 | 40.0 ±1.9 |
| Post-Course FCI Medians | 76.7 ±1.1 | 63.3± 2.9 |
| <g>median | 0.53± 0.03 | 0.39 ± 0.05 |
| G Medians | 0.47 ± 0.02 | 0.32 ± 0.03 |
Although the data show that the overall performance of students in the fall session was better than the performance of the summer students, the question remains as to whether the differences are significant. For data that conforms to a Gaussian distribution, the fairly well known Cohen d effect size is often used to characterize the difference in two distributions.15 For data like our values for G, which are not normally distributed, Cliff’s δ provides a similar measure.16 The Cliff δ for 2 samples is the probability that a value randomly selected from the first group is greater than a randomly selected value from the second group minus the probability that a randomly selected value from the first group is less than a randomly selected value from the second group. It is calculated as:
\[\delta = \frac{\#(x_1 > x_2 )− \#(x_1 < x_2 ) }{N_1 N_2} \tag{4} \]
where the symbol # indicates counting. The values of δ can range from –1, when all the values of the first sample are less than the values of the second, to +1, where all the values of the first sample are greater than the values of the second. A value of 0 indicates samples whose distributions completely overlap. By convention, |δ| ~ 0.2 indicates a “small” difference between the two samples, |δ| ~ 0.5 a “medium” difference, and |δ| ~ 0.8 a “large” one. 17 For our G values |δ| = 0.227 with a 95% confidence interval range18 of 0.136–0.314. Thus, the difference in G is small, but since the confidence interval range does not include zero it is statistically significant.
For the fall session, the correlation of FCI performance with student interest and background as has been studied.19 As shown here in the Appendix, except for their program of study (Question 1) the characteristics of the student population in the two sessions of the course are different. Therefore, we were surprised that when each course was examined separately, the normalized gains were the same within the uncertainties for each student characteristic and were also consistent with the overall values of Table I. Table II summarizes the median normalized gains for the two sessions for those characteristics that had a significant number of students in all categories and with different pre-course and post-course FCI scores (some of this data for the fall session also appeared in Ref 19). Also, recall that twice the stated uncertainty corresponds roughly to a 95% confidence interval.
Table II. Normalized Gains for Various Groups
| Student Category | Fall Session | Summer Session |
|---|---|---|
| <g>median | <g>median | |
| Taking the course because it is required | 0.47 ± 0.04 | 0.35 ± 0.05 |
| Taking the course for their own interest | 0.56 ± 0.11 | 0.32 ± 0.15 |
| Taking the course both because it is Required and for their own interest | 0.57 ± 0.04 | 0.41± 0.11 |
| Took Grade 12 Physics | 0.54 ± 0.03 | 0.35 ± 0.07 |
| Did not take Grade 12 Physics | 0.55 ± 0.04 | 0.45 ± 0.07 |
| Previously started but dropped the course | 0.48 ± 0.20 | 0.25 ± 0.14 |
| Had not previously started the course | 0.59 ± 0.03 | 0.42 ± 0.05 |
From Table II, the median Pre-Course FCI score for the fall session is greater than for the summer session by Δ = 13.3± 2.3 . As discussed in Ref. 19, fitting G vs the Pre-Course FCI scores for the fall session gave a small but positive slope of mfall = 0.00212 ± 0.00054 . Similar fits for the summer session gave a slope of msummer = 0.0018 ± 0.0021 , which is also positive but is zero within uncertainties. Coletta and Phillips propose that a “hidden variable”—the cognitive level of the students—is responsible for such non-zero slopes.20 Regardless of the cause, such slopes might be expected to give changes in the median normalized G of something on the order of Δ× mfall = 0.028± 0.009 or Δ× msummer = 0.02 ± 0.03 . The values are less than the uncertainty in the difference in <g>median (0.06) or the uncertainty in the difference in the values of the median of G (0.04) for the two courses. Thus, the effect of the differing Pre-Course FCI scores for the two courses appears to have a negligible impact on the values of the normalized gains. 8
IV. DISCUSSION
So far as we know, there is only one other study that compares student performance in compressed-format to regular-format in a post-secondary introductory physics course.21 This study used the Force and Motion Conceptual Evaluation (FMCE).22 However, in this study the type of pedagogy used in the different sessions of the course was somewhat different, although the instruction was more-or-less based on Physics Education Research in all versions. The results were that the normalized gains on the FMCE were somewhat less for the summer session than for either of the regular sessions that were studied.
There is also a study of summer intensive high-school physics courses for gifted students, which used the FCI and found that the gains were comparable to those of ordinary yearlong courses taken by average students. 23 There are studies of post-secondary courses in accounting24, and basic skills in math, English, and reading in U.S. community colleges. 25,26 The community college studies report that the compressed format is at least as effective as the regular format offerings, although they do not have a tool like the FCI to do a rigorous measurement of the effectiveness of the courses.
Our intuition was that the compressed 6-week format of the summer course does not allow adequate time for students to reflect upon and absorb the sometimes counterintuitive concepts of classical mechanics; some have compared this version of the course to trying to drink from a fire hose. Despite the fact that the present authors together have nearly 100 years of physics teaching experience, our intuition did not really correspond to the data. Although there are differences in the gains of the students, they are not nearly as dramatic as we had expected. This study, then, is another example of the importance of the methodology of Physics Education Research: teachers’ intuition is sometimes wrong but the data do not lie.
The fall session had two lecturers who alternated, and the summer session had a different lecturer. The two courses use almost identical pedagogy both in class and in the Practicals, and the three lecturers communicated regularly and occasionally observed each other’s classes. Hoellwarth and Moelter studied instructor effectiveness in a Studio Physics course over 9 quarters with 11 different instructors, and found that there were variations in the values of <g>mean for the same instructor for different quarters that were more significant than the variation between different instructors.27 Thus it is reasonable to assume that the small but statistically significant differences in performance of students in the two sessions studied here are largely due to the different formats of the course. Any differences due to the different effectiveness of the different instructors are perhaps at most second-order effects.
Finally, as stated in Ref. 19, we are continuing to collect this sort of data. We hope that with more students in the sample and better statistics we can revisit the question of normalized gains for different groups and sub-groups of students and the effectiveness of compressed-format compared to regular-format courses. Such longitudinal data will also allow us to get a better idea about the importance of the individual instructor or instructors in influencing student performance.
ACKNOWLEDGEMENTS
We particularly thank our Teaching Assistants, whom we call Instructors, whose great work in the Practicals is a vital part of the students’ learning. We also thank April Seeley in the Department of Physics for assistance in the collecting of the data of this study. We benefited from discussions about this work with David C. Bailey in the Department of Physics. We also acknowledge two anonymous reviewers for this journal whose comments helped strengthen the paper.
APPENDIX
We asked the students to self-report on the reason they are taking the course and some background information about themselves. Here we summarize that data.
1. “What is your intended or current Program of Study (PoST)?”
| Answer | Fall 2012 | Summer 2013 |
|---|---|---|
| Life Sciences | 88% | 90% |
| Physical and Mathematical Sciences | 9% | 8% |
| Other/Undecided 4% 2% | 4% | 2% |
2. “What is the main reason you are taking PHY131?”
| Answer | Fall 2012 | Summer 2013 |
|---|---|---|
| “Because it is required” | 32% | 60% |
| “For my own interest” | 16% | 12% |
|
“Both because it is required and for my own interest” |
52% | 28% |
3. “When did you graduate from high school?”
| Answer | Fall 2012 | Summer 2013 |
|---|---|---|
| 2012 78% 41% | 78% | 41% |
| 2011 | 9% 20% | 20% |
| 2010 | 5% | 21% |
| 2009 | 3% | 11% |
| Other/NA | 4% | 7% |
4. “Did you take Grade 12 Physics or an equivalent course elsewhere?”
| Answer | Fall 2012 | Summer 2013 |
|---|---|---|
| Yes | 75% | 61% |
| No | 25% | 39% |
5. “MAT135 or an equivalent calculus course is a co-requisite for PHY131. When did you take the math course?”
| Answer | Fall 2012 | Summer 2013 |
|---|---|---|
| “I am taking it now” | 81% | 5% |
| “Last year” | 10% | 53% |
|
“Two or more years ago” |
9% | 42% |
6. “Have your previously started but did not finish PHY131?”
| Answer | Fall 2012 | Summer 2013 |
|---|---|---|
| Yes | 4% | 15% |
| No | 96% | 85% |


