Antimatter

"The last level of metaphor in the Alice books [Alice in Wonderland, Through the Looking Glass] is this: that life, viewed rationally and without illusion, appears be be a nonsense tale told by an idiot mathematician. At the heart of things, science finds only a mad never-ending quadrille of Mock Turtle Waves and Gryphon particles. For a moment the waves and particles dance in grotesque, inconceivably complex patterns capable of reflecting their own absurdity. We all live slapstick lives ..." -- Martin Gardner, The Annotated Alice.

"The universe is a practical joke of the general at the expense of the particular." -- Aleister Crowley, The Book of Lies.

The Discovery of Antimatter

In 1932 there were three known "elementary particles:"

1. electron
2. proton
3. neutron

Then Carl Anderson discovered a new one. He was working with a cloud chamber, a forerunner to a bubble chamber.

We will illustrate Anderson's discovery by considering some bubble chamber interactions. The bubble chamber is essentially a "tub" of superheated liquid hydrogen. The hydrogen is not only the detector, but its protons form a target for an incoming beam of particles. When a charged object goes through the superheated hydrogen, it leaves behind a track of bubbles; for a cloud chamber, such as used by Anderson, the track of a charged particle similarly leaves behind a string of cloud droplets. In the bubble chamber experiments below, the proton targets of the hydrogen are being bombarded with a beam of high energy negatively charge pi mesons; these objects were, of course, unknown to Anderson in 1932.

To the right we show a bubble chamber photograph. A number of negatively charged pi mesons enters from the bottom; these are the beam particles, and have a momentum of 1.20 Gev/c. The mesons are moving at 99.331% of the speed of light.

One of the beam particles interacts with a proton to form a neutral lambda and a neutral K; both of these leave no track in the bubble chamber since they have no electric charge. Both of these neutral particles then decay into charged particles, which do leave tracks in the chamber. The lambda decays into a proton and a negatively charged pi meson; the K decays into the positively charged pi meson and a negatively charged pi meson.

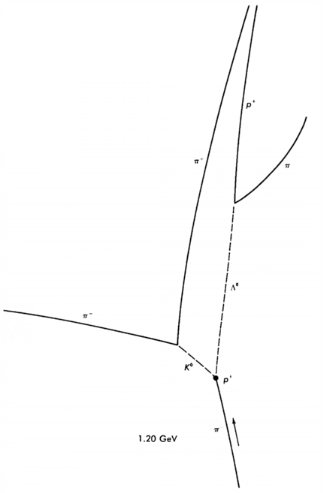
The diagram to the right shows a reconstruction of the interaction we see in the photograph.

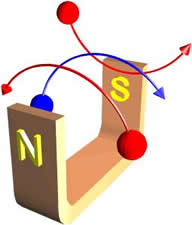
The reason for the curvature of the tracks is that there is a magnetic field directed into the plane of the photograph. The figure to the right shows the curvatures due to positive and negatively charged objects. Note that for positively and negatively charged particles moving from the left to right, their curvatures are in opposite directions. It will turn out to be useful later to note that the curvature of a positively charged object moving from right to left is identical to the curvature of the negative object moving from left to right. By measuring the radius of curvature of a track in a bubble chamber we can determine the momentum of the particle.

The faster the particle is moving, the less curvature there is in its trajectory. Thus, the beam particles in the above bubble chamber photograph are almost straight because they are moving at almost the speed of the light.

The new particle that Anderson discovered has the following properties:

• The mass equals the mass of the electron.
• The charge has the same magnitude as the electron's charge, but is positive instead of negative.
• The particle is always created in pairs with electrons.
• When this particle collides with an electron, both annihilate.

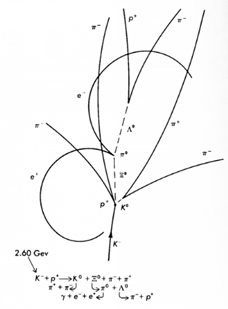
The figure to the right shows another bubble chamber photograph, this time in which "pair production" occurred. The beam is a 2.60 GeV/c negative K meson, again entering from the bottom.

In the reconstruction of the event, shown to the right, the electron is labelled e^- and the new particle that Anderson discovered is labelled e⁺. We call this new particle the antimatter electron or positron. It is now known that all so-called elementary particles have antimatter counterparts.

All the bubble chamber photographs and reconstructions of the events are from Harvey E. White, Modern College Physics 6th ed. (Van Nostrand Reinhold, 1972), pg 1011 and 1014.

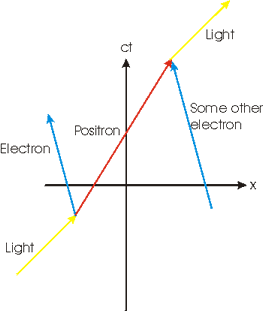
The figure to the right is the spacetime diagram for pair production and subsequent annihilation of the positron. Light energy comes in from the lower left. It creates a positron-electron pair; this is a conversion of the light energy into mass energy. The positron goes along until it collides with some other electron, which causes both to annihilate; the mass energy is converted into light energy.

When the positron was discovered, Heisenberg was particularly elated. It was already known that the neutron was unstable, decaying into a proton and an electron. This naturally led some people to think of a neutron as being made of a proton and electron. With the discovery of the positron, Heisenberg could just as easily think of the proton as being made of a neutron plus a positron. As he later wrote: "The symmetry between the proton and neutron was restored ... In the beginning was symmetry!" (Reference: Physics and Beyond, pg. 132.) In this view the proton and neutron are made of each other. This is an example of what we shall later be calling a bootstrap.

A simple Flash animation of pair production and annihilation may be found here. The animation will appear in a separate window. It requires Version 5 or better of the Flash player, which is available free from http://www.macromedia.com/. The file size if 4.7k.

Dirac's Theory of Antimatter

A comment by Dirac on why the positron was not discovered until 1932:

"Why did the experimentalists not see them? Because they were prejudiced against them. The experimentalists had been doing lots of experiments where particles were moving along curved tracks in a magnetic field. .... [They] sometimes saw the opposite curvature, and interpreted the tracks as electrons which happened to be moving into the source, instead of the positively charged particles coming out. That was the general feeling. People were so prejudiced against new particles that they never examined the statistics of these particles entering the source to see that there were really too many of them." -- Dirac, in J. Mehra, ed. The Physicist's Conception of Nature, pg. 12.

Note that Dirac is referring above to the fact we noted above that a negatively charged object moving from left to right in a magnetic field has the same curvature as a positively charged object moving from right to left.

If Dirac sounds a bit grumpy in the above quotation, there is a reason. He almost predicted the existence of the positron in 1930, before Anderson's discovery. He was musing about why the energy is always a positive number. He could think of no reason why this should be so. Applying a common physicists' assumption, that what is not forbidden is required, he concluded that there must be negative energy objects like electrons.

The next question, then, is why don't we observe these negative energy electrons. Dirac concluded that it must be because there is an infinitely dense totally homogeneous sea of these electrons everywhere in the universe. And since it is homogeneous it is unobservable.

Inayat Khan tells a Hindu story that has some relevance to this unobservable sea. A fish went to the Queen fish and asked: "I have always heard about the sea, but what is the sea? Where is it?" The Queen fish replied: "You live, move, and have your being in the sea. The sea is within you and without you, and you are made of sea and you will end in sea. The sea surrounds you as your own being." Reference: P. Reps, Zen Flesh, Zen Bones pg. 211.

Another example of a homogeneous and therefore unobservable structure is the now superfluous concept of an all-pervading luminiferous ether as a medium for light. Because this ether was homogeneous we could not detect it.

Now imagine that some light energy collides with a negative energy electron in Dirac's sea, knocking it into a positive energy state. This electron is observable. The hole it leaves in the sea is also observable, since it differs from the homogeneous negative energy sea around it. In fact, the hole will appear to have the mass of an electron. Further, its charge will appear to have the magnitude of the charge of the electron but will be positive. In fact, in Dirac's theory the hole is the positron!

When Dirac got this far, the positron was unknown. Thus he tried to interpret the hole as being a proton, but the mathematics of this theory didn't quite work out. When Anderson discovered the positron, Dirac immediately realised his theory described it perfectly. This theory of the positron is still routinely used.

The puzzle to the right was invented by Sam Loyd. The object of the puzzle is to re-arrange the tiles so that they are in numerical order.

The puzzle forms a model of how the positron moves in Dirac's theory. The numbered tiles represent the negative-energy electrons. The hole is the positron. When a negative-energy electron falls into the hole, the hole appears to have moved to another position.

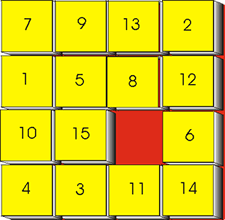
What appears to be the annihilation of the positron when it collides with some other electron, then, is just the electron falling into the hole, giving up its energy as light.

Feynman's Theory of Antimatter

In 1949 Richard Feynman devised another theory of antimatter.

The spacetime diagram for pair production and annihilation appears to the right. An electron is travelling along from the lower right, interacts with some light energy and starts travelling backwards in time. An electron travelling backwards in time is what we call a positron. In the diagram, the electron travelling backwards in time interacts with some other light energy and starts travelling forwards in time again. Note that throughout, there is only one electron.

A friend of mine finds the image of an electron travelling backwards in time, interpreted by us as a positron, to be scary.

Feynman in his original paper proposing this theory wrote: "It is as though a bombardier flying low over a road suddenly sees three roads and it is only when two of them come together and disappear again that he realizes that he has simply passed over a long switchback in a single road." (Physical Review 76, (1949), 749.)

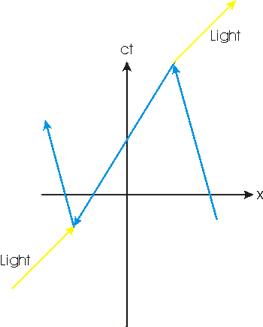
Note that Feynman's theory is yet another echo of the fact, noted above, that a negatively charged object moving from left to right in a magnetic field has the same curvature as a positive object moving from right to left.

Feynman's theory is mathematically equivalent to Dirac's, although the interpretations are quite different. Which formalism a physicist uses when dealing with antimatter is usually a matter of which form has the simplest structure for the particular problem being solved.

Note that in Feynman's theory, there is no pair production or annihilation. Instead the electron is just interacting with electromagnetic radiation, i.e. light. Thus the whole process is just another aspect of the fact that accelerating electric charges radiate electric and magnetic fields; here the radiation process is sufficiently violent to reverse the direction of the electron's travel in time.

Nambu commented on Feynman's theory in 1950: "The time itself loses sense as the indicator of the development of phenomena; there are particles which flow down as well as up the stream of time; the eventual creation and annihilation of pairs that may occur now and then is no creation or annihilation, but only a change of direction of moving particles, from past to future, or from future to past." (Progress in Theoretical Physics 5, (1950) 82).

About Formally Equivalent Descriptions

Above we noted that Feynman's theory of antimatter is formally equivalent to Dirac's theory. This means that the mathematics of either theory can be manipulated into the other one. Here is a nearly trivial example to illustrate. We say that there are two variables that describe some physical property: y and t. Perhaps y is the position of some object being acted on by various forces, and t is the time.

We imagine that some theory gives the relation between the two variables as:

Then we "read" the mathematics of the theory as a statement that tells us what the position of the object is for various times. We say that t is the independent variable, and that y is dependent on x. Here are some values:

Independent Variable	Dependent Variable
1	8
2	11
3	16

Some other theory relates y and t according to:

Now we "read" the mathematics as a statement that says that for a given position of the object we can calculate when it was at that position. We say that now y is the independent various and t the dependent variable.

Independent Variable	Dependent Variable
8	1
11	2
16	3

But the two equations are mathematically and formally equivalent to each other. Thus although the way we view whatever process is being described differently depending on which equation is being used, the underlying formalism is the same.

When we return to Quantum Mechanics, we will see another example of two formally equivalent theories. These are the Heisenberg form of Quantum Mechanics and the Schrödinger one. There we shall see that despite the formal equivalence, both Heisenberg and Schrödinger felt strongly about which one is "correct."

A Representation of Both Theories of Antimatter

"Day and Night" by M.C. Escher. Note that both Dirac's and Feynman's theory of antimatter are represented. This was not Escher's intention, of course. Instead, in this and much of his work he was focusing on figure-ground studies.

Thousands of years ago Chuang Tsu wrote a commentary that seems apropos for both Escher's drawing and these two theories of antimatter:

"It comes out from no source, it goes back in through no aperture. It has reality yet no place where it resides; it has duration yet no beginning or end. Something emerges, though through no aperture - this refers to the fact that it has reality. It has reality yet there is no place where it resides - this refers to the dimension of space. It has duration but no beginning or end - this refers to the dimension of time. There is life, there is death, there is a coming out, there is a going back in - yet in the coming out and going back its form is never seen." (23, Watson trans.)

The figure to the right is a classic figure-ground study. Looked at one way the figure is a vase; from another perspective it is two faces. The distinction between the figure and the ground defining the figure is reminiscent for me of Dirac's infinite homogeneous sea of negative energy electrons.

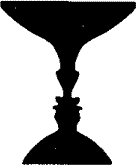
Gestalt psychology uses figures like these. Some people have difficulty in seeing one or the other of the images, and these psychologists have devised techniques to aid people in learning to see both and switch back and forth between them. Of course, their goal in this is quite a bit more than just seeing both images in a figure-ground study.

Although most people can switch back and forth between the two ways of seeing the above figure, we can not see both at once. This reminds of so-called wave-particle duality for electrons: we can think of the electron as a wave or as a particle but can't think of it as both at once. The actual figure, though, is both the vase and the faces; similarly the electron is both a wave and a particle.

Why Is This Topic In The SYMMETRY Part of the Syllabus?

Recall that in the very early days of the universe, matter was created through pair production of electrons-positrons and protons-anti-protons. Does this mean that one-half of the matter in the universe is antimatter? Almost all experts in this field know the answer to the question. The problem is that some of the experts think the answer is "Yes" and others think the answer is "No."

Recall that a simple model of a hydrogen atom is a positively charged proton with a negatively charged electron in orbit around it. We can similarly have an anti-hydrogen atom with a negatively charged antiproton with a positively charged positron in orbit around it. This anti-hydrogen atom has been experimentally produced.

Similarly, we can have anti-helium, anti-molecules, etc.

It is certainly possible that there are antimatter galaxies, with anti-solar systems and maybe anti-people. In Dirac's theory we might say that the anti-people are holes in an infinite sea of negative energy people. They, of course, would say that we are holes in an infinite sea of negative energy anti-people.

Imagine that we get in radio contact with intelligent aliens from, say, the Planet of the Apes. With painstaking effort we establish a common language and end up in a state of good communication. One of the things that we want to communicate is the difference between left and right. It turns out that the only way to do this is to use the violation of mirror symmetry by weak interactions. So, we can have the aliens construct an apparatus like Madame Wu used in her classic experiment, and with that it is possible to define right and left.

However, if they are in an antimatter part of the universe, their anti-Madame Wu apparatus will get the definition backwards. So, if we set up a face to face meeting with the aliens and, having told them about some of our customs, when we meet they want to shake hands with us and extend their left hand, we better run!

Before the 1950's the validity of mirror symmetry was considered to be a nearly self-evident truth; you may recall that this symmetry is sometimes called conservation of parity. Yet another symmetry that used to be believed to be true is called charge conjugation: if we turn all particles into their anti-particles (and all anti-particles into their particles) everything will work the same. Now we know that neither parity or charge conjugation are completely conserved. But from the anti-Madame Wu experiments we can say that together they are conserved. Turn all particles into their anti-particles and then turn the whole system into its mirror image; the result will work the same. We shall have more to say about this in the next section of the syllabus titled Time's Arrow.

Symmetry and Conservation

In the previous section we sometimes talked about a symmetry, such as mirror symmetry, and sometimes describe the same circumstance in terms of a conservation of some quantity. There turns out to be a very close connection between symmetry and conservation.

For every symmetry, there is a corresponding conservation. The converse is also true: for every conservation, there is a corresponding symmetry.

For example, symmetry under spatial translation is equivalent to conservation of momentum. Symmetry under time translation is equivalent to conservation of energy. And symmetry under rotations is equivalent to conservation of angular momentum

Charge Conjugation, Parity, and Time Reversal

Above we indicated that in weak interactions such as used in Madame Wu's experiment, if we take the apparatus and construct a mirror image of it, and then take all the particles of the apparatus and turn them into their corresponding antiparticles, this new apparatus will work exactly like the original one. Sometimes, this is called CP Invariance, where the C stands for charge conjugation and the P for parity ie. mirror reflection.

There is a meson called the K ⁰, which is electrically neutral and decays via the weak interaction into either:

• an electron, a positive pi meson and an anti-neutrino; or
• a positron, a negative pi meson, and a neutrino.

It turns out that the second mode is slightly preferred over the first.

The K ⁰ has an antimatter pair, the K bar⁰, which also decays via these same two modes, and for the anti-K meson the second mode is also slightly preferred over the first.

If one draws pictures of these decays, including the helicity states of the decay products, it isn't too difficult to realise that these experimental facts means that CP Invariance is violated.

However, according to our best understanding, if we:

• Turn all particles into their antiparticles (C); and
• Subject the decays to a mirror reflection (P); and
• Reverse the direction of time (T)

the combination of these three operations leaves the decay invariant. This is sometimes called CPT Invariance.

We summarize the invariance and symmetries that we have been discussing:

• Space translation, time translation, rotation: believed to be absolutely true.
• Mirror reflection (P): true for gravitational, electromagnetic, and strong interactions; not true for weak interactions.
• Turning particles into antiparticles + turning antiparticles into particles (C) + P: true for all interactions except for a small subset of weak interactions.
• C + P + reversing the direction of time (T): believed to be absolutely true.

A Great Question From a Former Student

Is the existence of symmetry due to the existence of non-symmetry?

A Final Speculation

Wheeler once called Feynman in the middle of the night, saying "There is only one electron in the universe!" The figure to the right shows what he meant. We assume the universe is closed. In Feynman's theory of antimatter, all the worldlines of the electrons and positrons connect so throughout there is only the one electron. This "explains" a mysterious fact: all electrons have totally identical properties.