7: Symmetries and Particle Physics
- Page ID
- 15044
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Symmetries in physics provide a great fascination to us – one of the hang-ups of mankind. We can recognize a symmetry easily, and they provide a great tool to classify shapes and patterns. There is an important area of mathematics called group theory, where one studies the transformations under which an object is symmetric. In order to make this statement seem less abstract, let me look at a simple example, a regular hexagon in a plane. As can be seen below, this object is symmetric (i.e., we can’t distinguish the new from the old object) under rotations around center over angles of a multiple of \(60^\circ\), and under reflection in any of the six axes sketched in the second part of the figure.
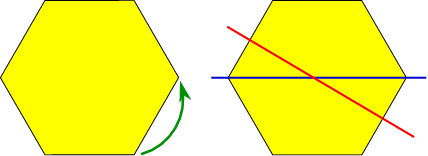
The symmetries of a hexagon
- 7.1: Importance of Symmetries - Noether’s theorem
- There are important physical consequences of symmetries in physics, especially if the dynamics of a system is invariant under a symmetry transformation. There is a theorem, due to Emily Noether, one of the most important (female) mathematicians of this century, that states that for any continuous symmetry there is a conserved quantity.
- 7.2: Lorenz and Poincaré Invariance
- One of the most common continuous symmetries of a relativistic theory is Lorentz invariance, i.e., the dynamics is the same in any Lorentz frame. The group of Lorentz transformations can be decomposed into two parts: (1) Boosts, where we go from one Lorentz frame to another, i.e., we change the velocity. and (2) Rotations, where we change the orientation of the coordinate frame.
- 7.3: Internal and Space-Time Symmetries
- The invariance of the dynamics is such that J is the conserved quantity, which means that we should not just rotate in ordinary space, but in the abstract “intrinsic space” where S is defined. This is something that will occur several times again, where a symmetry has a combination of a space-time and intrinsic part.
- 7.4: Discrete Symmetries
- Let us first look at the key discrete symmetries – parity P (space inversion) charge conjugation C and time-reversal T .
- 7.5: The CPT Theorem
- There is a fairly strong proof that only minimal physical assumptions (locality, causality) that the product of C , P and T is a good symmetry of any theory. Up to now experiment has not shown any breaking of this product. We would have to rethink a lot of basic physics if this symmetry is not present. I am reasonably confident that if breaking is ever found there will be ten models that can describe it within a month!
- 7.6: CP Violation
- The first experimental confirmation of symmetry breaking was found when studying the β− decay of Co-60.
- 7.9: Representations of SU(3) and Multiplication Rules
- A very important group is SU(3), since it is related to the color carried by the quarks, the basic building blocks of QCD. The transformations within SU(3) are all those amongst a vector consisting of three complex objects that conserve the length of the vector. These are all three-by-three unitary matrices.
- 7.10: Broken Symmetries
- Of course one cannot propose a symmetry, discover that it is not realized in nature (“the symmetry is broken”), and expect that we learn something from that about the physics that is going on. But parity is broken, and we still find it a useful symmetry! That has to do with the manner in which it is broken, only weak interactions – the exchange of W± and Z bosons – break them. Any process mediated by strong, electromagnetic or (probably) gravitational forces conserves the symmetry.
- 7.11: Gauge Symmetries
- There is of a certain class of local symmetries (i.e., symmetries of the theory at each point in space and time) called gauge symmetries and are usually labelled by the local symmetry group. Local symmetries are not directly observable, and do not have immediate consequences. They allow for a mathematically consistent and simple formulation of the theories, and in the end predict the particle that are exchanged – the gauge particles.


