3.5: The Human Eye

The eye is an adaptive optical device.

3.4.1 Anatomy

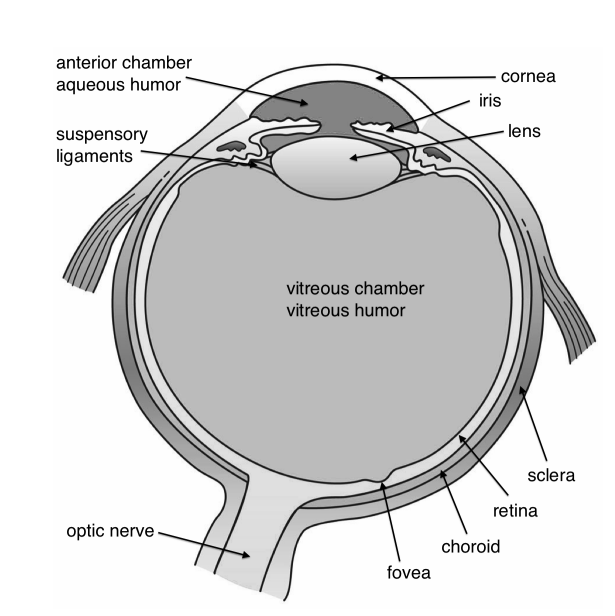
The human eye is made of an almost spherical (24 mm long and 22 mm across) gelatinous substance called the vitreous humor with refractive index 1.337, surrounded by a white shell, the sclera (Figure \(\PageIndex{3}\)). At the front, the sclera has an opening with a transparent lens called the cornea, with for green light an index of refraction of 1.376. Most of the bending of the rays takes place at the air-cornea interface and this is why it is difficult to see under water (n_water = 1.33). After passing the cornea, the rays reach the aqueous humour (n ≈1.336) with the iris (i.e. pupil). It can expand or contract from a 2 mm (bright sun) to 8 mm (low light) diameter to adapt to the light intensity. The iris gives colour to the eye. After the iris, the rays reach the flexible crystalline lens which has the size of a bean (9 mm in diameter, and 4 mm thick in unaccommodated condition). Its index of refraction varies from 1.406 in the centre to 1.386 at the edge.

Figure \(\PageIndex{3}\): Cross section of a human eye (from Wikimedia Commons by Holly Fischer / CC BY).

3.4.2 Working of the eye

The entire eye can very accurately be treated as two lenses in contact, of which the crystalline lens can change its focal length. Often the system is approximated by only a single lens. In unaccommodated condition, the first focal distance of the lens system is f_o = 16 mm as measured from the cornea. The second focal distance is equal to the length of the eye: f_i = 24 mm. These focal distances are different, because the refractive indices of the surrounding medium (air and vitreous humour) differ. The power of the intact, unaccommodated eye lens system is, according to (2.5.35), (2.5.39):

\[\mathfrak{D}=\frac{n_{v h}}{f_{2}}=\frac{1.337}{0.0243}=55 \text { Diopter. } \nonumber \]

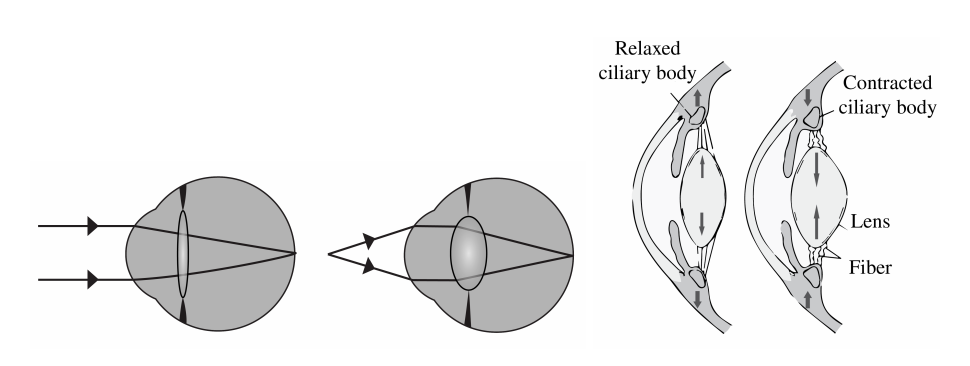
In relaxed condition the lens focuses light coming from infinity on the retina. When the object is closer, the eye muscles contract due to which the crystalline lens becomes more convex and the focal length of the system decreases, as seen on the right of Figure \(\PageIndex{4}\). At a certain point, the object will be too close to be focused on the retina. This is called the near point of the eye. Due to the loss of elasticity of the muscle, the near point moves from 7 cm for teens to 100 cm for a 60-year-old. Figure \(\PageIndex{4}\) shows the optical rays entering the eyes, for two configurations: an object at infinity and an object nearby. The so-called normal near point is at 25 cm. The far point is the furthest object which is imaged on the retina by the unaccommodated eye. For the normal eye the far point is at infinity.

Figure \(\PageIndex{4}\): Left: Optical rays showing how an eye accommodates by changing its focal length. Right: Relaxed and contracted muscle at the crystalline lens needed for this accommodation.(Left: adapted from Wikimedia Commons Erin Silversmith / BY-NC-SA 2.5 Generic. Right: adapted from Sjaastad O.V., Sand O. and Hove K. (2010) Physiology of domestic animals, 2nd edn., Oslo: Scandinavian Veterinary Press).

3.4.3 Retina

The retina is composed of approximately 125 million photoreceptor cells: the rods and the cones. The rods are highly sensitive black and white (intensity) sensors, while the cones are colour sensitive for the wavelengths 390 nm - 780 nm. UV light is absorbed by the lens (people whose lens is removed because of cataract can "see" UV light). The fovea centralis is the most sensitive centre of the retina with a high density of cones. The eyes move continuously to focus the image on this area. The information is transferred by the optical nerve, placed at the back of the eye, where it causes a blind spot.

3.4.4 Dioptric Power of a lens

For a combination of two thin lenses, it is not so easy to derive the resulting focal length from the individual focal length of the lenses. It is easier to consider the dioptric power. For a single lens the dioptric power is defined by:

\[\mathfrak{D}=\frac{1}{f}=\left(n_{i}-1\right)\left(\frac{1}{R_{1}}-\frac{1}{R_{2}}\right) \nonumber \]

with R₁ and R₂ the radii of the thin lens and n_i the index of refraction of the glass. Because for two lenses in contact, the focal length is given by:

\[\frac{1}{f}=\frac{1}{f_{1}}+\frac{1}{f_{2}}, \nonumber \]

the combined power of the two lenses is the sum of the individual powers:

\[\mathfrak{D}=\mathfrak{D}_{1}+\mathfrak{D}_{2} \nonumber \]

A lens of focal length \(f_{1}=10 \mathrm{~cm}\) has a dioptric power \(\mathfrak{D}_{1}=10 \mathrm{D}\). If it is in contact with a negative lens of dioptric power \(\mathfrak{D}_{2}=-10 \mathrm{D}\), the resulting power is \(\mathfrak{D}=0\), equivalent to a parallel sheet of glass.

3.4.5 Eyeglasses

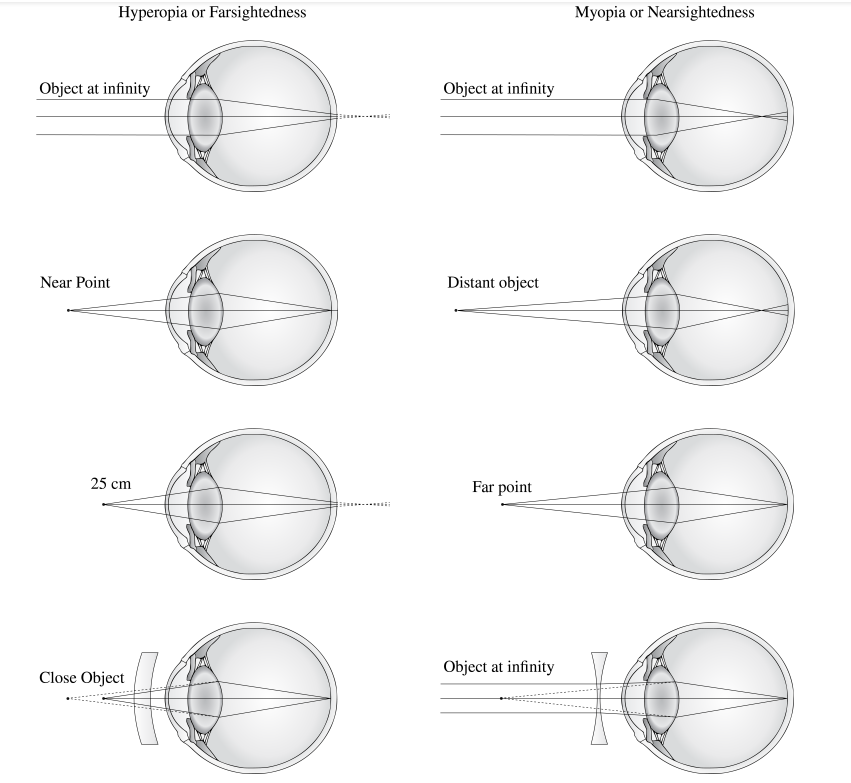
The eye can suffer from imperfections as seen in Figure \(\PageIndex{5}\). We discuss the most common imperfections and their solutions.

a. Myopia or Nearsightedness. A myopic eye has too short focal distances (has too high power) so that distant objects are focused in front of the retina by the unaccommodated eye. The far point is thus not at infinity, but closer. This can be corrected by a negative lens. Suppose the far point is at \(2 \mathrm{~m}\). If the concave lens makes a virtual image of a distant object at distance \(2 \mathrm{~m}\) in front of the cornea, the unaccommodated eye can see it clearly. The lens Law (2.5.44), with \(s_{o}=-\infty\) implies then \(f_{i}=s_{i}=-2 \mathrm{~m}\). Hence the required power of the lens is: \[\mathfrak{D}=\frac{1}{f}=-0.5 \text { Diopter. } \nonumber \] The lens is best put in the front focal plane of the unaccomodated eye, i.e. at approximately 16 \(\mathrm{mm}\) in front of the cornea. (Since the distance of the retina to the eye lens is roughly \(22 \mathrm{~mm}\) and the refractive index of the vitrous humor is \(1.337\), this implies a focal distance in air of the unaccomodated eye of \(22 / 1.337 \approx 16 \mathrm{~mm}\) ). The reason is that in this case the magnification of the eye and the negative lens together are the same as for the uncorrected eye. To see this, draw a ray from the top of the object through the centre of the negative lens. This will then be made parallel to the optical axis by the eye lens; the distance of this ray to the optical axis is the image size on the retina. This ray will end up at the same point of the retina as when the negative lens is taken out, because it is not refracted by this lens.

Contact lenses are very close to the eye lens and hence the total power of the eye with a contact lens is simply the sum of the power of the eye and the contact lens.

b. Hyperopia or Farsightedness. In this case a distant object is imaged by the unaccommodated eye behind the retina, i.e. the back focal distance of the unaccommodated eye is larger than the depth of the eye. Close objects can not be imaged on the retina, hence the near point is relatively far from the cornea. In order to bend the rays more, a positive lens is placed in front of the eye. Suppose that a hyperopic eye has near point at distance \(125 \mathrm{~cm}\). For an object at \(s_{o}=-25 \mathrm{~cm}\) to have virtual image at \(s_{i}=-125 \mathrm{~cm}\), so that it can be seen, the focal length must satisfy \[\frac{1}{f}=-\frac{1}{s_{o}}+\frac{1}{s_{i}}=\frac{1}{0.25}-\frac{1}{1.25}=\frac{1}{0.31} \text {, } \nonumber \] hence the power must be \(\mathfrak{D}=1 / f=+3.2\) Diopter.

Figure \(\PageIndex{5}\): Correction of farsighted (left) and nearsighted (right) eye (adapted from Wikimedia Commons by Gumenyuk I.S. / CC BY-SA 4.0).

c. Presbyopia. This is the lack of accommodation of the eye as is common in people over 40. It results in an increase in the distance between the near point and the retina. This defect affects all images. Presbyopia is usually corrected by glasses with progressive correction, the upper part of glass used for distance vision and the lower part for near vision.

d. Astigmatism. In this case the focal distances for two directions perpendicular to the optical axis are different. It is attributed to a lack of symmetry of revolution of the cornea. This is compensated by using glasses which themselves are astigmatic.

3.4.6 New Correction Technique

In recent years, to correct eye defects such as myopia and astigmatism, technology has been developed to change the local curvatures of the surface of the cornea using an excimer laser. The laser is computer-controlled and causes photo-ablation in parts of the cornea.