3.6: Magnifying Glasses
- Page ID
- 57090
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
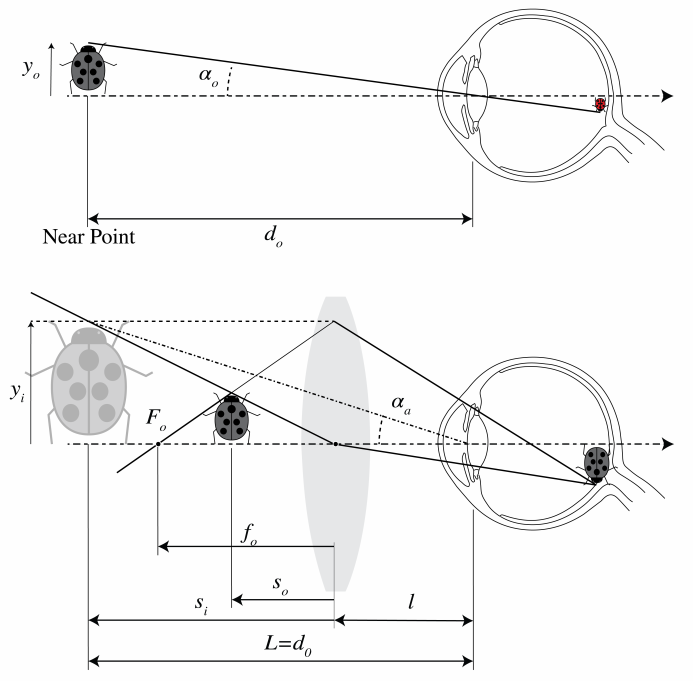
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)A magnifying glass causes an image on the retina which is larger than without the magnifier. In principle, the image on the retina can be increased by simply bringing the object closer to the eye (reduce \(\left|s_{o}\right|\) at fixed \(s_{i}\) ). But \(\left|s_{o}\right|\) can not be smaller than the near point \(d_{o}\), which we take here to be \(25 \mathrm{~cm}\). It is desirable to use a lens that makes a magnified erect image at a distance to the eye greater than \(d_{o}\). This can be achieved by a positive lens with the object closer to the lens than the first focal point, thereby producing a magnified virtual image. An example is given in Figure \(\PageIndex{1}\).

3.5.1 Magnifying Power
The magnifying power MP or angular magnification \(M_{a}\) is defined as the ratio of the size of the retinal image obtained with the instrument and the size of the retinal image as seen by the unaided eye at normal viewing distance \(d_{o}\). To estimate the size of the retinal image, we compare in both cases where the chief ray through the top of the object and the centre of the pupil of the eye hits the retina. Since the distance between the eye lens and the retina is fixed, the ratio of the image size on the retina for the eye with and without magnifying glass is: \[\mathrm{MP}=\frac{\alpha_{a}}{\alpha_{u}}, \nonumber \] where \(\alpha_{a}\) and \(\alpha_{u}\) are the angles between the optical axis and the chief rays for the aided and the unaided eye, respectively, as shown in Figure \(\PageIndex{2}\). Working with these angles instead of distances is in particular useful when the virtual image of the magnifying glass is at infinity. Using \(\alpha_{a} \approx y_{i} / L\) and \(\alpha_{u} \approx y_{0} / d_{0}\) with \(y_{i}\) and \(y_{0}\) positive and \(L\) the positive distance from the image to the eye (with as requirement : \(L \geq d_{o}\) ), we find \[\mathrm{MP}=\frac{y_{i} d_{0}}{y_{0} L} . \nonumber \] Since \(s_{i}<0\) and \(f_{o}<0\) we have, \[\frac{y_{i}}{y_{o}}=\frac{s_{i}}{s_{o}}=1+\frac{s_{i}}{f_{o}}, \nonumber \] where we used the lens equation for the magnifying glass. We have \(s_{i}=-\left|s_{i}\right|=-(L-\ell)\), where \(C\) is the distance between the magnifying glass and the eye. Hence, \(( \(\PageIndex{2}\) )\) becomes: \[\begin{aligned} \mathrm{MP} &=\frac{d_{0}}{L}\left[1+\frac{L-\iota}{\left|f_{o}\right|}\right] \\ &=\frac{d_{0}}{L}[1+\mathfrak{D}(L-\iota)], \end{aligned} \nonumber \] where \(\mathfrak{D}\) is the power of the magnifying glass.
1. \(\ell=\left|f_{o}\right|\) : the magnifying power is then \(\mathrm{MP}=d_{0} \mathfrak{D}\).
2. \(\ell=0\) : hence \(L=d_{0}\) is smallest while MP is maximum:
\[\left.\mathrm{MP}\right|_{\ell=0, L=d_{0}}=d_{0} \mathfrak{D}+1 \nonumber \]
3. The object is at the focal point of the magnifier \(\left(s_{0}=f_{o}\right)\), so that the virtual image is at infinity \((L=\infty)\) and hence
\[\left.\operatorname{MP}\right|_{L=\infty}=d_{0} \mathfrak{D}, \nonumber \] for every distance \(l\) between the eye and the magnifying glass. The rays are parallel, so that the eye views the object in a relaxed way. This is the most common use of the magnifier.
In practice \(d_{0} \mathfrak{D}=d_{o} /\left|f_{o}\right|\) is much larger than 1 , so that MP is similar in the three cases.
3.5.2 Nomenclature
Normally magnifiers are expressed in terms of the magnifying power when \(L=\infty\) (case 3 above). For example, a magnifier with a power of 10 Diopter has a MP equal to \(2.5\) or \(2.5 \times\). In other words, the image is \(2.5\) times larger than it would be if the object would be at the near point of the unaided eye.

